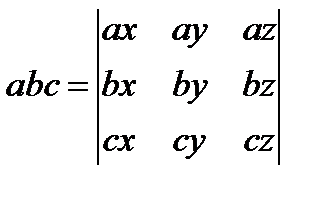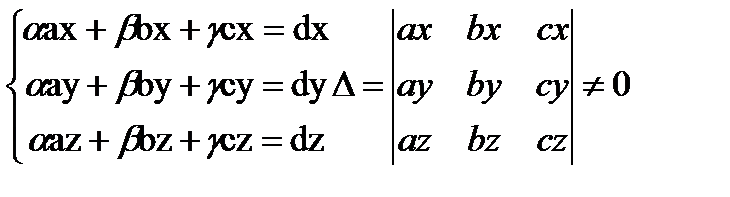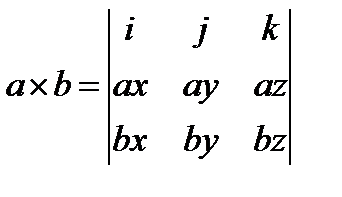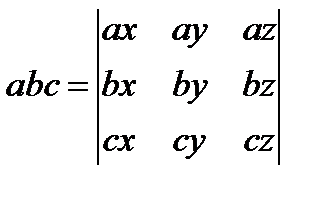Построение базисов в конкретных линейных пространствах.

L=V³ – пр-во геометрических векторов.

Утверждение. Базис в L образует любая система из трёх некомпланарных векторов.

Размерность L равна 3.

Док-во. Пусть S={a,b,c} некомпланарные векторы, что S линейно независима. Покажем, что S полна в L= V³, т.е. "вÎ V³ есть разложение по системе S: d=aa+bb+gc. Запишем векторы a, b, c, d через координаты в базисе {i,j,k}. a=(ax,ay,az), b=(bx,by,bz), c=(cx,cy,cz), d=(dx,dy,dz).

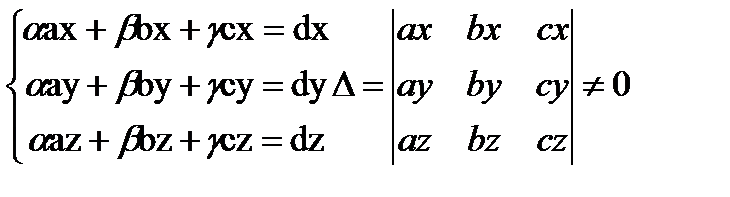
D<>0, т.к. векторы a, b, c не компланарны.

Система с не нулевым определителем имеет единственное решение, значит разложение существует.

Следствие. В пр-ве V³ любая система из 4 и более векторов линейно зависима.

L=Rⁿ – арифметическое n-мерное пространство.

Утверждение. dim Rⁿ =n; пример базиса в Rⁿ даёт система S={e1,e2,…,en}, где e1=(1,0,…,0), e2=(0,1,0,…,0)… en=(0,0,…,1) канонический базис в Rⁿ.

Док-во. Докажем полноту. "x=(x1,x2,…,xn)ÎRⁿ имеем равентсво x=x1e1+x2e2+…+xnen. Действительно x=(x1,0,…,0)+(0,x2,…,0)+…+(0,0,…,xn)=x1(1,0,…,0)+x2(0,1,0,…,0)+…+xn(0,0,…,1)=x1e1+x2e2+…+xnen. Пусть 0=a1e1+a2e2+…+anen. Покажем, что все коэффициенты нули a1=an=0. Действительно 0=(0,0,…,0)=a1(1,0,…,0)+ a2(0,1,0,…,0)+…+an(0,0,…,1)=(a1,a2,…,an) => a1=a2=…= an=0. Вывод: S – линейно независима и полна, т.е. S – базис в Rⁿ.

Следствие. Размерность Rⁿ = n. В Rⁿ любая система из m>=n+1 векторов линейно зависима.

L=Pn – пр-во многочленов степени не выше n.

L=Pn={p(t)=p0+p1t+…+pntⁿ: pkÎR}

Утверждение. Размерность Pn=n+1, при этом пример базиса даёт система: S={1,t,…,tⁿ}.

Док-во. "p(t)ÎPn имеем p(t)=p0+p1t+…+pntⁿ – разложение по системе S с коэффициентами p0, p1,…, pn. "pÎPn имеем p(t)=p0e0(t)+p1e1(t)+…+pnen(t) разложение по системе S. Линейная независимость. Если a0e0(t)+a1e1(t) +…+anen(t)=0, т.е. a0+a1t+…+antⁿ º 0, то покажем, что a0=a=…=an=0. Дифференцируем это множество n раз. Получаем a0=a1=…=an=0.

Пусть L – линейное пространство, МÌL, М – подпространство. Тогда само М является линейным пространством. Обозначим n=dimL, m=dimM.

Теорема. Размерность подпространства не выше размерности пространства. m<=n. Если m=n, то подпространство совпадает со всем пространством. Если m<n, то базис подпространства М можно достроить до базиса всего пространства L.

Док-во. Sm={e1,e2,…,em} – базисв М. Тогда Sm – линейно не зависимая система векторов из L и число векторов в Sm не больше, чем размерность L=n, т.е. m<=n. Пусть m=n, тогда базис Sm подпространства М будет линейно независимой системой векторов в L с числом векторов равным n=dimL, значит такая система образует базис в L, т.е. Sm базис в М и L. Следовательно, её линейная оболочка L(Sm)=L, т.к. Sm базис в L. Значит, в М=L. Пусть m<n, тогда базис Sn подпространства М будет линейно независимой системой векторов в L, но не базисом, значит Sm не полна в L, т.е. существует вектор e_m+1ÎL\L(sm). Добавим этот вектор в систему. S_m+1={e1,…,em,e_m+1}. Эта система линейно независима. Если m+1=n, то S_m+1, базис в L. Если m+a<n, то S_m+1 не полна в L и можно найти вектор e_m+2ÎL, e_m+2ÎL(S_m+1). Добавив его получим систему S_m+2={e1,…,em,e_m+1,e_m+2} (линейно независима). Если m+2=n, то S_m+2 базис в L. Продолжая построение в результате получим систему Sn линейно независимую, она и есть базис в L.

Рангом r(S) системы векторов S называется размерность её линейной оболочки: r(S)=dimL(S).

Базой (максимальной линейно независимой подсистемой) системы S называется её подсистема S` со свойствами:

1) S` - линейно независима;

2) все векторы из S линейно выражаются через векторы из S`.

Замечание. Если система S линейно независима, то она сама является своей базой.

Теорема. База системы векторов образует базис в её линейной оболочке.

Док-во. Пусть S – система векторов, S` - её база. Тогда S` линейно независима, любой вектор из L(S) линейно выражается через векторы из S, а они в свою очередь линейно выражаются через векторы системы S`. В итоге любой вектор xÎL(S) линено выражается через векторы из S`. Это означает, что S` полна в L(S), следовательно S` - базис в L(S).

Следствие. Все базы содержат одинаковое число векторов, равное рангу системы.

Следствие. Если S` линейно независимая подсистема системы S и число векторов в S` равно рангу S, то S` - база системы.

Замечание. Если система линейно независима, то размерность её линейной оболочки (её ранг) равен числу векторов в ней, т.к. она сама является своей базой.

Пусть L – линейное пространство, S={e1,…,ek}, S1={f1,…,fm} – системы векторов из L.

Теорема. Если все векторы из S1 линейно выражаются через векторы из S, то ранг системы S1 не больше, чем ранг S (r(S1)<=r(S)).

Док-во. Покажем, что L(S1)ÌL(S). Для "xÎL(S1) есть линейное выражение этого вектора через векторы из S1. Но они линейно выражаются через векторы из S. В итоге получаем линейное выражение вектора xÎL(S1) через векторы из S, т.е. xÎL(S). Доказали, что если xÎL(S1), то xÎL(S). L(S) – линейное пространство, L(S1) – подпространство => dimL(s1)<=dimL(S), r(S1)<=r(S).

Элементарными преобразованиями системы векторов преобразования вида:

1) перестановка двух векторов в системе;

2) умножение одного из векторов системы на число не равное нулю;

3) добавление к одному из векторов другого с некоторым коэффициентом.

Замечание. Если одна система получена из другой с помощью элементарных преобразований, то и та в свою очередь получается из новой с помощью обратных элементарных преобразований.

Теорема. Если одна система получена из другой с помощью элементарных преобразований, то их ранг одинаков.

Док-во. Если S1 получена из S элементарными преобразованиями, то векторы из S1 линейно выражаются через векторы из S. r(S1)<=r(S). В свою очередь векторы из S выражаются через векторы из S1 с помощью обратных элементарных преобразований, значит r(S)<=r(S1). Значит r(S)=r(S1).

Замечание. При элементарных преобразованиях база системы может исчезнуть.

Вектора

Вектор – это направленный прямолинейный отрезок, т.е. отрезок, имеющий определённую длину и определённое направление.

Длиной вектора называется длина отрезка.

Вектор, длина которого равна нулю, называется нулевым вектором.

Вектор, длина которого равна единице, называется единичным вектором.

Векторы a и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

Вектор, соединяющий начало одного вектора с концом другого вектора называется суммой этих векторов.

Под разностью векторов a и b понимается вектор c=a-b такой, что b+c=a.

Произведением вектора a на скаляр l называется вектор lа, который имеет длину |l|*|a|, коллинеарен вектору а, имеет направление вектора а, если l>0 и противоположное, если l<0.

Линейные операции над векторами обладают следующими свойствами:

1) a+b=b+a;

2) (a+b)+c=a+(b+c);

3) l1(l2*a)= l1*l2*a;

4) (l1+l2)*a=l1*a+l2*a;

5) l(a+b)= la+lb.

Проекцией точки М на ось l называется основание М1 перпендикуляра ММ1, опущенного из точки на ось.

Проекцией вектора на AB ось l называется положительное число |AB|, если вектор A1B1 и ось l одинаково направлены и отрицательное число, если вектор А1В1 и ось l противоположно направлены.

Св-ва.

1. Проекция вектора а на ось l равна произведению модуля вектора а на косинус угла j между вектором и осью, т.е. прla=|a|*cosj.

Следствие. Проекция вектора на ось положительна(отрицательна), если вектор образует с осью острый(тупой) угол, и равна нулю, если этот угол – прямой.

Следствие. Проекции равных векторов на одну и ту же ось равны между собой.

2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.

3. При умножении вектора а на число l его проекция на ось также умножается на это число.

Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.

 

a=ax*I+ay*j+az*k. Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа ax, ay, az называются координатами вектора a, т.е. координаты вектора есть его проекции на соответствующие координатные оси.

|a|=Ö(ax²+ay²+az²), т.е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.

cos²a+ cos²b+ cos²g=1, т.е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.

Скалярным произведением двух ненулевых векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними.

Св-ва.

1) ab=ba;

2) (la)b=l(ab);

3) a(b+c)=ab+ac;

4) a²=|a|²;

5) если векторы a и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю.

a*b=axbx+ayby+azbz. Скалярное произведение векторов равно сумме произведений их одноимённых координат.

Векторным произведением вектора а на вектор b называется вектор с, который:

1) перпендикулярен векторам а и b;

2) имеет длину, численно равную площади параллелограмма, построенного на векторах a и b как на сторонах, т.е. |c|=|a|*|b|*sinj, где j угол между векторами а и b;

3) векторы a, b и c образуют правую тройку.

Св-ва.

1. При перестановке сомножителей векторное произведение меняет знак.

2. l(axb)=(la)xb=ax(lb).

3. Два не нулевых вектора a и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

4. (a+b)xc=axc+bxc.

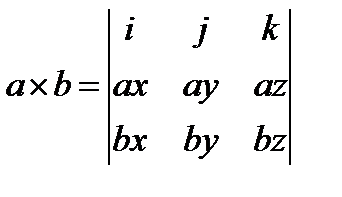
Смешанное произведение представляет собой число.

Св-ва.

1. (axb)c=(bxc)a=(cxa)b.

2. (axb)c=a(bxc).

3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т.е. abc=-acb.

4. Смешанное произведение ненулевых векторов a, b и с равно нулю тогда и только тогда, когда они компланарны.