Матрицы и операции над ними
Матрицей называется прямоугольная таблица чисел вида
 ,
,
имеющая n столбцов и m строк. Числа aij,  ;
; 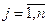 , называют элементами матрицы А. Если нужно указать размеры матрицы, то пишут
, называют элементами матрицы А. Если нужно указать размеры матрицы, то пишут  . Иногда матрицу обозначают в виде
. Иногда матрицу обозначают в виде
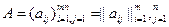 = (aij).
= (aij).
Если 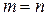 , то матрицу А называют квадратной, а число n - ее порядком. Квадратная матрица порядка n называется диагональной, если
, то матрицу А называют квадратной, а число n - ее порядком. Квадратная матрица порядка n называется диагональной, если 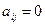 при любых
при любых
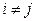 :
:
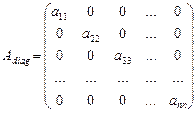 .
.
Диагональная матрица, у которой все элементы главной диагонали 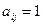 ,
, 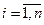 , называется единичной и обозначается буквой Е:
, называется единичной и обозначается буквой Е:
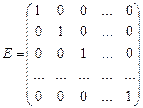
Матрица вида
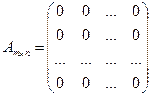
2
называется нулевой и обозначается О.
Квадратная матрица 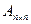 называется треугольной, если все элементы ее, расположенные по одну сторону от главной диагонали, равны нулю. Матрица
называется треугольной, если все элементы ее, расположенные по одну сторону от главной диагонали, равны нулю. Матрица 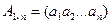 называется вектором-строкой, а матрица
называется вектором-строкой, а матрица 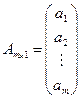 называется вектором-столбцом,
называется вектором-столбцом,  - одноэлементная матрица.
- одноэлементная матрица.
Матрица, полученная из данной 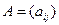 заменой каждой ее строки столбцом с тем же номером, называется транспонированной, к данной и обозначается
заменой каждой ее строки столбцом с тем же номером, называется транспонированной, к данной и обозначается 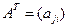 . например, если
. например, если 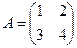 , то
, то 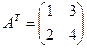 , а если
, а если 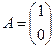 , то
, то  . Матрица
. Матрица  называется симметрической, и обозначается А ¢, если
называется симметрической, и обозначается А ¢, если 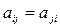 . Для такой матрицы
. Для такой матрицы 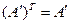 .
.
Определение. Матрицы 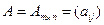 ,
, 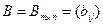 равны между собой,
равны между собой, 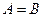 , если
, если 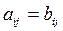 ,
, 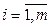 ;
; 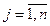 .
.
Произведением матрицы 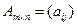 на число a называется матрица
на число a называется матрица 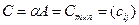 , для которой c
, для которой c  .
.
Пример. 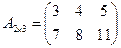 ,
, 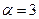
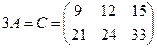 .
.
Суммой двух матриц 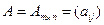 и
и 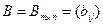 называется матрица
называется матрица 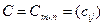 , для которой
, для которой 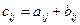 .
.
Пример. 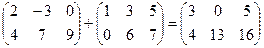 .
.
Аналогично определяется разность матриц.
Операции сложения матриц и умножения матрицы на число являются линейными операциями, так как обладают следующими свойствами:
1. 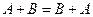 ;
;
2. 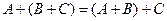
3. A+O=A;
4. 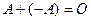 ;
;
5. 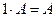 ;
;
6. 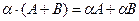 ;
;
7.  ;
;
8. 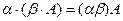 ;
;
9. 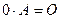 .
.
Упражнение. Доказать, что 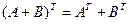 .
.
Над матрицами можно производить элементарные преобразования:
1. перестановка местами двух строк или столбцов;
2. умножение всех элементов строки или столбца на число 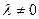 ;
;
3. прибавление ко всем элементам одной строки или столбца соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
 Две матрицы
Две матрицы 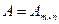 и
и 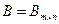 - эквивалентные, если одна из них получается из другой при помощи элементарных преобразований. Пишут А ~ В. При помощи элементарных преобразований матрицу
- эквивалентные, если одна из них получается из другой при помощи элементарных преобразований. Пишут А ~ В. При помощи элементарных преобразований матрицу  можно привести к элементарному каноническому виду В, т.е. к матрице, у которой существуют
можно привести к элементарному каноническому виду В, т.е. к матрице, у которой существуют 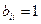 ,
, 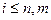 , а
, а 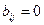 ,
, 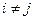 . Например:
. Например:
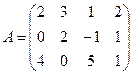 ~
~ 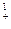
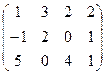 ~
~ 
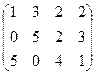 ~
~ 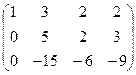 ~
~
~ 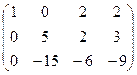 ~
~ 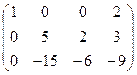 ~
~ 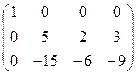 ~
~ 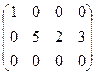 ~
~
~ 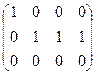 ~
~ 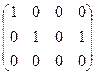 ~
~ 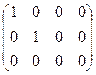 = B.
= B.
Если число столбцов матрицы 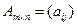 равно числу строк матрицы
равно числу строк матрицы 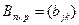 , то определяется произведение этих матриц
, то определяется произведение этих матриц 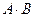 , при котором получается матрица
, при котором получается матрица 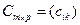 такая, что
такая, что
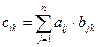
(поэлементное умножение i -ой строки матрицы А на k -й столбец матрицы В).
Пример. Пусть 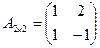 и
и 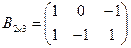 .
.
Тогда
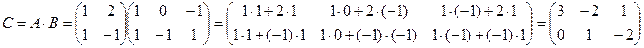
Однако здесь произведение 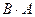 не существует, так как
не существует, так как  , где 3 - число столбцов для матрицы В, а 2 - число строк для А.
, где 3 - число столбцов для матрицы В, а 2 - число строк для А.
Если 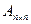 и
и 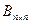 , то существуют матрицы
, то существуют матрицы 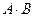 и
и 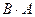 , при этом
, при этом 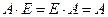 . В общем случае
. В общем случае 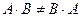 . Например, если
. Например, если  ,
, 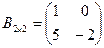 , то
, то 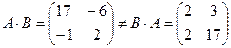 .
.
Умножение матриц обладает следующими свойствами:
1. 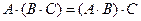 ;
;
2. 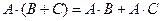 ;
;
3. 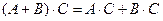 ;
;
4. 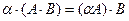 .
.
Образцы решения контрольных работ.
Задание №1
Вычислить А 2 - 3 АВ, где
А = 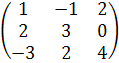 В =
В = 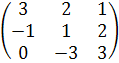
Решение.
А 2 = А ∙ А = 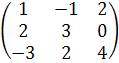 ∙
∙ 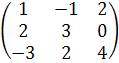 =
=
(Для получения элемента, стоящего в первой строке и в первом столбце, матрицы А 2перемножим соответствующие элементы первой строки матрицы А и элементы первого столбца этой матрицы, т.е первый элемент первой строки матрицы А умножим на первый элемент первого столбца матрицы А; второй элемент первой строки матрицы А на второй элемент первого столбца этой матрицы; третий элемент первой строки матрицы А умножим на третий элемент первого столбца матрицы,и их произведения сложим;
для получения элемента, стоящего в первой строке и во втором столбце, перемножим соответствующие элементы первой строки матрицы А и элементы второго столбца матрицы А и их произведения сложим и т.д.)=
= 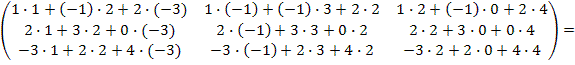
= 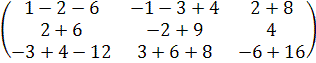 =
= 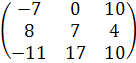
Аналогичным способом находим произведение матриц А и В:
А ∙ В = 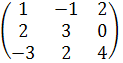 ∙
∙ 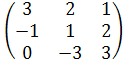 =
=
= 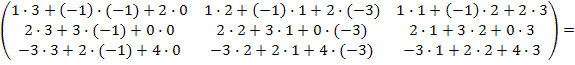
= 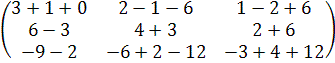 =
= 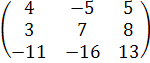
Затем находим
3∙ А ∙ В = 3∙ 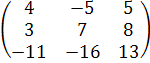 =(чтобы умножить матрицу на число надо каждый элемент матрицы умножить на это число)=
=(чтобы умножить матрицу на число надо каждый элемент матрицы умножить на это число)= 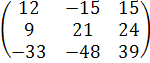 .
.
Тогда А 2 - 3 АВ =  -
- 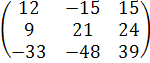 =(чтобы вычесть две матрицы, надо вычесть их соответствующие элементы)=
=(чтобы вычесть две матрицы, надо вычесть их соответствующие элементы)=
= 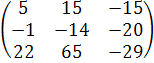 .
.
Задание №2
Решить систему уравнений
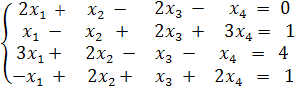 (1)
(1)
1) методом Гаусса;
2) по правилу Крамера;
3) матричным способом.
Решение.
1) Метод Гаусса.
Составим расширенную матрицу, соответствующую системе (1) и приведем ее к треугольному виду. Для этого запишем расширенную матрицу данной системы:
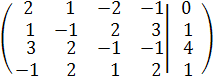
и приведем эту матрицу к треугольному виду с помощью элементарнях преобразований, а именно:
- перестановкой строк;
- умножением элементов строки матрицы на число;
- сложение соответствующих (стоящих на одинаковых местах) элементов двух строк и помещение сумм этих элементов на место соответствующих элементов одной из складываемых строк.
Чтобы привести матрицу к треугольному виду надо получить нули на месте элементов, стоящих под главной диагональю. Сперва получим нули в первом столбце во второй, третьей и четвертой строках, т.е. надо изменить вторую, третью, четвертую строки. Так как первая строка не изменяется, изменения в других строках будем производить относительно нее: выберем на главной диагонали неизменяемой строки главный элемент, в нашем примере это 2. Если в столбце, в котором мы хотим получить нули, имеется 1, то для облегчения счета, строку с1 на первом месте лучше поставить на место первой расширенной матрицы и сделать ее, тем самым, неизменяемой.В нашем примере вторая строка содержит на первом месте 1. Поменяем ее с первой строкой. Эту операцию обозначим следующим образом: 
 С 2 С 1,здесь С 2 – вторая строка, С 1 – первая строка, при этом получим эквивалентную матрицу
С 2 С 1,здесь С 2 – вторая строка, С 1 – первая строка, при этом получим эквивалентную матрицу

Теперь главным элементом будет 1.Обведем его в квадрат.Чтобы получить на месте 2 во второй строке 0, надо каждый элмент первой строки умножить на (-2) и сложить с соответствующим элементом второй строки и их сумму записать на место соответствующего элемента второй строки. Эту операцию обозначим следующим образом:
С 2:= -2∙ С 1 + С 2,
здесь:= - это оператор присваивания, т.е. значение выражения с правой стороны записывается на место величины, стоящей слева. Получим при этом эквивалентную матрицу
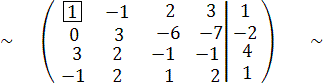
Чтобы получить вместо 3 в третьей строке нуль, проделаем операцию
С 3:= -3∙ С 1 + С 3,
а чтобы получить вместо (-1) в четвертой строке нуль, проделаем операцию
С 4:= С 1 + С 4.
В результате получим эквивалентную матрицу
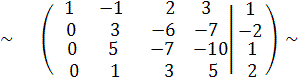
Теперь нужно получить нули во втором столбце в строках три и четыре, т.е. изменяемыми будут третья и четвертая строки. Выберем главный элемент в неизменяемой строке во втором столбце и который стоит на диагонали (в примере это 3), но среди изменяемых строк имеется строка, в которой во втором столбце стоит 1, поменяем ее со строкой, в которой мы выбрали главный элемент (т.е. надо поменять местами вторую и четвертую строчки)

 С 4 С 2,
С 4 С 2,
при этом получим эквивалентную матрицу
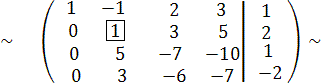
Теперь главным элементом будет 1. Заключим его в квадрат.Чтобы получить вместо 5 число нуль, проделаем операцию
С 3:= -5∙ С 2 + С 3,
а чтобы получить вместо 3 нуль, проделаем операцию
С 4:= -3 С 2 + С 4,
при этом получим эквивалентную матрицу
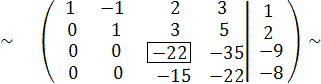
Осталось получить нуль в третьем столбце четвертой строки. Главный элемент выбераем в третьем столбце на диагонали (это -22)(так как изменяемой будет только четвертая строка, и среди изменяемых строк в третьем столбце нет единицы, то -22 и будет главным элементом). Чтобы получить вместо 15 нуль, проделаем следующую операцию
С 4:=- 15∙ С 3 +22∙ С 4,
при этом получим эквивалентную матрицу
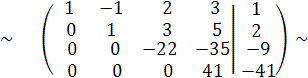
(разделив последнюю строчку полученной матрицы на 41,т.е. С 4:= С 4: 41,
получим эквивалентную матрицу)
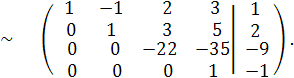
Запишем по полученной матрице эквивалентную систему уравнений:
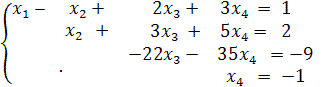
Из последнего уравнения имеем
x 4 = - 1.
Подставляя это значение в предпоследнее уравнение, получим
- 22 x 3 - 35∙(- 1) = - 9. Отсюда находим
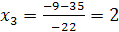
Тогда из второго уравнения получим для x 2 равенство
x 2 +3∙2 + 5∙(-1) = 2 или x 2 = 2 – 6 +5 =1.Аналогично,подставляя найденные значения для x 2, x 3 и x 4 в первое уравнение,получим
x 1 - 1 + 2∙2 +3∙(-1) = 1 или x 1 = 1.
Ответ: 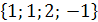 .
.
Задание №3
Решить методом Гаусса.
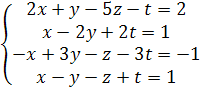 .
.
Составим расширенную матрицу и приведем ее с помощью элементарных преобразований к треугольному виду.

 A =
A = 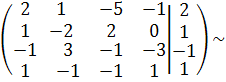 С 2 С 1
С 2 С 1 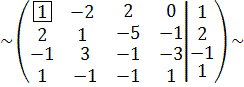
С 2:= -2∙ С 1 + С 2, С 3:= С 1 + С 3, С 4:= - С 1 + С 4

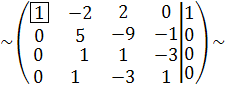
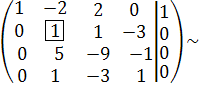
С 3:= -5 С 2 + С 3, С 4:= - С 1 + С 4
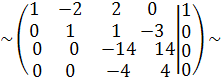
Разделим третью строку на 14, а четвертую на 4
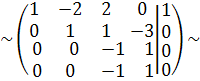 С 4:= - С 3 + С 4
С 4:= - С 3 + С 4 
r = rang A = 3 < 4. Следовательно, система имеет бесконечное множество решений, из которых 3 являются базисными. Положим x, y, z за базисные решения, так как базисный минор  . Тогда находим общее решение системы.Для этого составим по полученной матрице систему уравнений
. Тогда находим общее решение системы.Для этого составим по полученной матрице систему уравнений
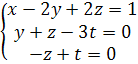 =>
=> 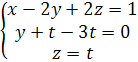 =>
=> 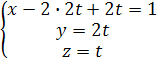
=> 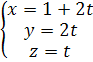 .
.
Обозначим: t = С. Тогда система имеет множество решений:
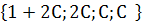 ,где С-параметр решения.
,где С-параметр решения.
Задание №4
Задания к контрольной работе №1
Задание №1
1.Даны матрицы А = 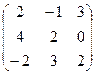 и В =
и В = 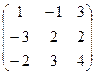 .
.
Вычислить А 2 + ВА+2В.
2.Даны матрицы А = 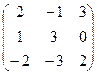 и В =
и В = 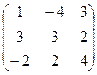 .
.
Вычислить А 2 + АВ-3В.
3.Даны матрицы А = 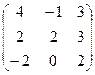 и В =
и В = 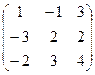 .
.
Вычислить В 2 + АВ- 3 А.
4.Даны матрицы А = 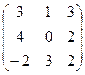 и В =
и В =  .
.
Вычислить В 2 - 3 В + ВА.
5.Даны матрицы А = 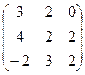 и В =
и В = 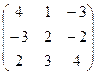 .
.
Вычислить В 2 +2А + ВА.
6.Даны матрицы А = 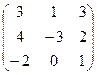 и В =
и В = 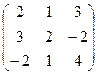 .
.
Вычислить 2 А 2 -3В + ВА.
7.Даны матрицы А = 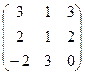 и В =
и В = 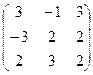 .
.
Вычислить В 2 - 2 В + 3ВА.
8.Даны матрицы А = 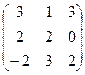 и В =
и В = 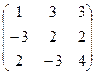 .
.
Вычислить В 2 -3В + 2 АВ.
9.Даны матрицы А = 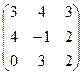 и В =
и В = 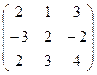 .
.
Вычислить 2А 2 - 3 В + ВА.
10.Даны матрицы А = 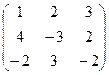 и В =
и В = 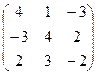 .
.
Вычислить В 2 -4А + ВА.
Задание №2
Решить системы линейных алгебраических уравнений
а) методом Гаусса;
б) по правилу Крамера;
в) матричным способом.
1. 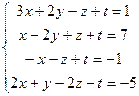 6.
6. 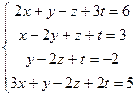
2. 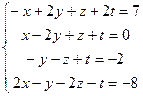 7.
7. 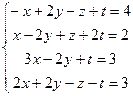
3.  8.
8. 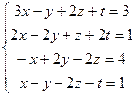
4.  9.
9. 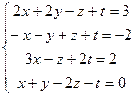
5. 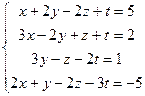 10.
10. 
Задание №3
Решить систему линейных алгебраических уравнений
а) методом Гаусса;
1. 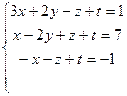 2.
2. 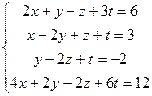
3. 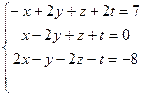 4.
4. 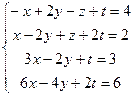
5. 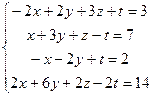 6.
6. 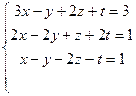
7. 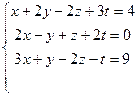 8.
8. 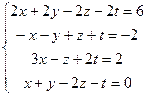
9. 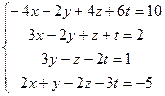 10.
10. 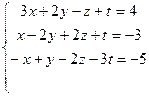
Задание №4
Найти собственные числа и собственные векторы матрицы А.
1. 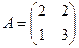 2.
2. 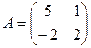
3. 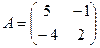 4.
4. 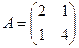
5.  6.
6. 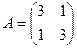
7. 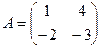 8.
8. 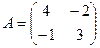
9. 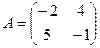 10.
10. 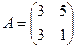
УДК 517
Зубков А.Н.,Павлова М.Н.
Матрицы и их применение /А.Н.Зубков,М.Н.Павлова.–Ростов –на-Дону:Издательский центр ДГТУ,2011.-41с.
Учебное пособие написано в соответствии с учебной программой по высшей математике для технических специальностей ДГТУ и его филиалов. Цель работы – отразить применение таких основных понятий линейной алгебры как матрица и определитель при решении систем линейных алгебраических уравнений.
В пособии приводятся основные понятия и теоремы, которые необходимы в практическом применении при решения задач контрольных работ первого семестра студентами очно-заочной и вечерней форм обучения.
Рецензенты:
…………………………………канд.физ.-мат.наук, доцент ЮФУ………………..
………………………………………………доцент ДГТУ
В В Е Д Е Н И Е
…..Предлагаемое учебное пособие написано в соответствии с учебной программой по высшей математике для технических специальностей ДГТУ и его филиалов. Цель работы – отразить применение таких основных понятий линейной алгебры как матрица и определитель при решении систем линейных алгебраических уравнений, которые необходимы студентам первого семестра прежде всего при выполнении контрольных заданий для очно-заочной и вечерней форм обучения.
Работа состоит из пяти разделов,которые выделены в виде параграфов. В первых четырех из них приводятся основные понятия и формулируются теоремы, используемые при решении задач. В необходимых случаях даются примеры, поясняющие смысл определений и теорем. Затем приводятся подробные решения сформулированных задач со ссылкой на приведенные ранее формулы, определения и теоремы. Даются упражнения для закрепления усвоения основных понятий. В заключительном пятом параграфе излагаются подробно решения типовых задач,связанных с решением систем линейных алгебраических уравнений и которые необходимы при решении контрольных заданий.В заключение приводится список типовых заданий для студентов, необходимых для успешного усвоения ими данного материала
Содержание
ВВЕДЕНИЕ
§ 1.Матрицы и операции над ними.
§ 2.Опредедителб матрицы и обратная матрица.
§ 3.Решение систем линейных алгебраических уравнений.
§ 4.Характеристическое уравнение. Собственные векторы и собственные значения матрицы An‰n.Приведение матрицы An‰n к диагональному виду.
§ 5.Образцы решения контрольных работ.
Рекомендуемая литература
1.Кострикин А.И.Введение в алгебру/А.И..Кострикин.-М.:Наука,1977.
2.Ефимов Н.В. Квадратичные формы и матрицы/Н.В.Ефимов.-Наука,1964.
3.Шипачев В.С. Высшая математика./В.С. Шипачев.- М.: Высшая школа,1985.
Матрицы и операции над ними
Матрицей называется прямоугольная таблица чисел вида
 ,
,
имеющая n столбцов и m строк. Числа aij,  ;
; 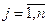 , называют элементами матрицы А. Если нужно указать размеры матрицы, то пишут
, называют элементами матрицы А. Если нужно указать размеры матрицы, то пишут  . Иногда матрицу обозначают в виде
. Иногда матрицу обозначают в виде
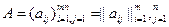 = (aij).
= (aij).
Если 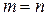 , то матрицу А называют квадратной, а число n - ее порядком. Квадратная матрица порядка n называется диагональной, если
, то матрицу А называют квадратной, а число n - ее порядком. Квадратная матрица порядка n называется диагональной, если 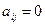 при любых
при любых
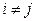 :
:
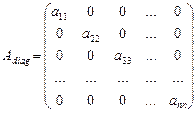 .
.
Диагональная матрица, у которой все элементы главной диагонали 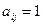 ,
, 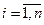 , называется единичной и обозначается буквой Е:
, называется единичной и обозначается буквой Е:
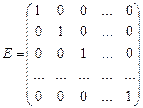
Матрица вида
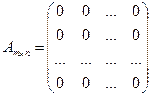
2
называется нулевой и обозначается О.
Квадратная матрица 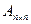 называется треугольной, если все элементы ее, расположенные по одну сторону от главной диагонали, равны нулю. Матрица
называется треугольной, если все элементы ее, расположенные по одну сторону от главной диагонали, равны нулю. Матрица 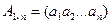 называется вектором-строкой, а матрица
называется вектором-строкой, а матрица  называется вектором-столбцом,
называется вектором-столбцом,  - одноэлементная матрица.
- одноэлементная матрица.
Матрица, полученная из данной 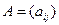 заменой каждой ее строки столбцом с тем же номером, называется транспонированной, к данной и обозначается
заменой каждой ее строки столбцом с тем же номером, называется транспонированной, к данной и обозначается 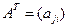 . например, если
. например, если 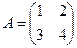 , то
, то 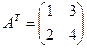 , а если
, а если 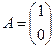 , то
, то  . Матрица
. Матрица 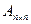 называется симметрической, и обозначается А ¢, если
называется симметрической, и обозначается А ¢, если 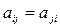 . Для такой матрицы
. Для такой матрицы 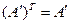 .
.
Определение. Матрицы 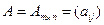 ,
, 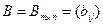 равны между собой,
равны между собой, 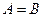 , если
, если 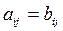 ,
, 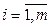 ;
; 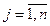 .
.
Произведением матрицы 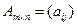 на число a называется матрица
на число a называется матрица 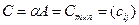 , для которой c
, для которой c  .
.
Пример. 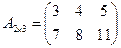 ,
, 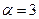
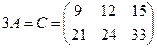 .
.
Суммой двух матриц 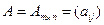 и
и 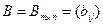 называется матрица
называется матрица 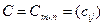 , для которой
, для которой 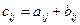 .
.
Пример. 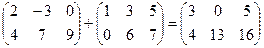 .
.
Аналогично определяется разность матриц.
Операции сложения матриц и умножения матрицы на число являются линейными операциями, так как обладают следующими свойствами:
1. 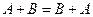 ;
;
2. 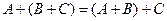
3. A+O=A;
4. 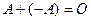 ;
;
5. 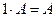 ;
;
6. 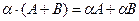 ;
;
7.  ;
;
8. 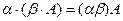 ;
;
9. 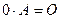 .
.
Упражнение. Доказать, что 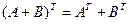 .
.
Над матрицами можно производить элементарные преобразования:
1. перестановка местами двух строк или столбцов;
2. умножение всех элементов строки или столбца на число 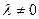 ;
;
3. прибавление ко всем элементам одной строки или столбца соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
 Две матрицы
Две матрицы 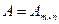 и
и 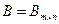 - эквивалентные, если одна из них получается из другой при помощи элементарных преобразований. Пишут А ~ В. При помощи элементарных преобразований матрицу
- эквивалентные, если одна из них получается из другой при помощи элементарных преобразований. Пишут А ~ В. При помощи элементарных преобразований матрицу  можно привести к элементарному каноническому виду В, т.е. к матрице, у которой существуют
можно привести к элементарному каноническому виду В, т.е. к матрице, у которой существуют 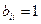 ,
, 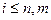 , а
, а 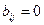 ,
, 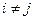 . Например:
. Например:
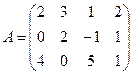 ~
~ 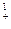
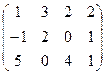 ~
~ 
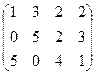 ~
~ 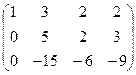 ~
~
~ 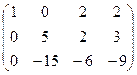 ~
~ 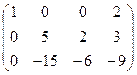 ~
~ 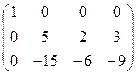 ~
~ 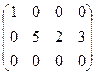 ~
~
~ 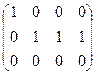 ~
~ 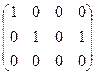 ~
~ 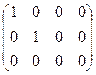 = B.
= B.
Если число столбцов матрицы 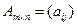 равно числу строк матрицы
равно числу строк матрицы 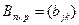 , то определяется произведение этих матриц
, то определяется произведение этих матриц 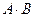 , при котором получается матрица
, при котором получается матрица 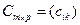 такая, что
такая, что
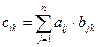
(поэлементное умножение i -ой строки матрицы А на k -й столбец матрицы В).
Пример. Пусть 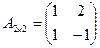 и
и 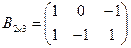 .
.
Тогда
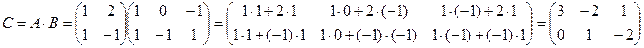
Однако здесь произведение 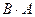 не существует, так как
не существует, так как  , где 3 - число столбцов для матрицы В, а 2 - число строк для А.
, где 3 - число столбцов для матрицы В, а 2 - число строк для А.
Если 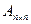 и
и 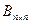 , то существуют матрицы
, то существуют матрицы 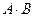 и
и 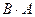 , при этом
, при этом 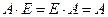 . В общем случае
. В общем случае 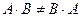 . Например, если
. Например, если  ,
, 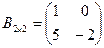 , то
, то 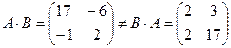 .
.
Умножение матриц обладает следующими свойствами:
1. 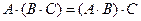 ;
;
2. 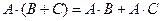 ;
;
3. 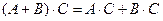 ;
;
4. 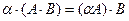 .
.
Определитель матрицы и обратная матрица
Каждой матрице можно сопоставить число det A, | A | или D, которое называют определителем матрицы и находят следующим образом:
1. 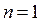 .
. 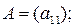
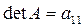 ;
;
2. 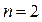 .
.
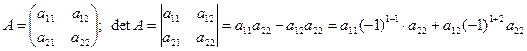 ;
;

4. В общем случае, если A = 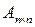 , то det A находится с помощью разложения Лапласа:
, то det A находится с помощью разложения Лапласа: 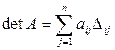
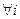 ,
, 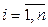 , где Aij =
, где Aij = 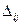 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 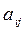 , т.е.
, т.е.
! ij = 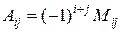 ,
,
где 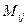 - минор элемента
- минор элемента 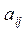 , т.е. определитель квадратной матрицы А, полученный из А вычеркиванием i -ой строки и j -ого столбца.
, т.е. определитель квадратной матрицы А, полученный из А вычеркиванием i -ой строки и j -ого столбца.
Пример. 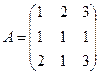
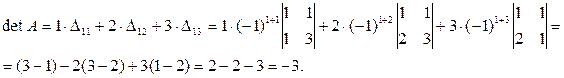
Можно показать, что 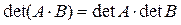 (использовать правило Лапласа) и что
(использовать правило Лапласа) и что 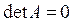 Û если имеются в А нулевая строка или нулевой столбец или две пропорциональные строки или столбца.
Û если имеются в А нулевая строка или нулевой столбец или две пропорциональные строки или столбца.
Наибольший из порядков миноров 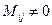 матрицы An ‰ n называется ее рангом и обозначается r,
матрицы An ‰ n называется ее рангом и обозначается r,  или rang A. Очевидно, что
или rang A. Очевидно, что 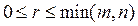 . Минор, порядок которого определяет ранг матрицы, называется базисным. Ранг матрицы А равен числу единиц на главной диагонали канонической матрицы, к которой приводится матрица А путем элементарных преобразований. Например,
. Минор, порядок которого определяет ранг матрицы, называется базисным. Ранг матрицы А равен числу единиц на главной диагонали канонической матрицы, к которой приводится матрица А путем элементарных преобразований. Например,
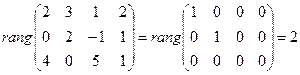 .
.
Квадратная матрица A =. An ‰ n называется невырожденной, если 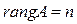 , т.е. базисный минор совпадает с определителем матрицы
, т.е. базисный минор совпадает с определителем матрицы 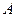 . В противном случае, когда rang А < n, A называется вырожденной матрицей. В этом случае
. В противном случае, когда rang А < n, A называется вырожденной матрицей. В этом случае 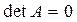 .
.
Матрица B = 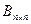 , удовлетворяющая условиям
, удовлетворяющая условиям
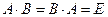 ,
,
называется обратной к An ‰ n и обозначается



 ,
, ;
; 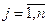 , называют элементами матрицы А. Если нужно указать размеры матрицы, то пишут
, называют элементами матрицы А. Если нужно указать размеры матрицы, то пишут  . Иногда матрицу обозначают в виде
. Иногда матрицу обозначают в виде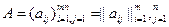 = (aij).
= (aij).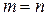 , то матрицу А называют квадратной, а число n - ее порядком. Квадратная матрица порядка n называется диагональной, если
, то матрицу А называют квадратной, а число n - ее порядком. Квадратная матрица порядка n называется диагональной, если 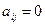 при любых
при любых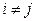 :
: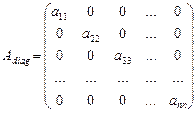 .
. ,
, 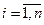 , называется единичной и обозначается буквой Е:
, называется единичной и обозначается буквой Е: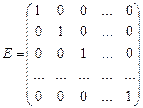
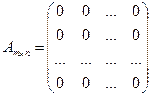
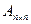 называется треугольной, если все элементы ее, расположенные по одну сторону от главной диагонали, равны нулю. Матрица
называется треугольной, если все элементы ее, расположенные по одну сторону от главной диагонали, равны нулю. Матрица 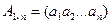 называется вектором-строкой, а матрица
называется вектором-строкой, а матрица  называется вектором-столбцом,
называется вектором-столбцом,  - одноэлементная матрица.
- одноэлементная матрица.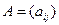 заменой каждой ее строки столбцом с тем же номером, называется транспонированной, к данной и обозначается
заменой каждой ее строки столбцом с тем же номером, называется транспонированной, к данной и обозначается 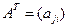 . например, если
. например, если 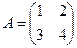 , то
, то 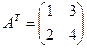 , а если
, а если 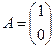 , то
, то  . Матрица
. Матрица 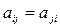 . Для такой матрицы
. Для такой матрицы 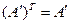 .
.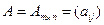 ,
, 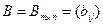 равны между собой,
равны между собой, 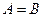 , если
, если 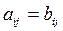 ,
, 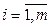 ;
; 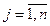 .
.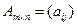 на число a называется матрица
на число a называется матрица 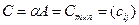 , для которой c
, для которой c  .
.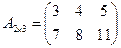 ,
, 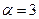
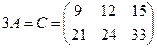 .
.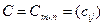 , для которой
, для которой 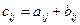 .
.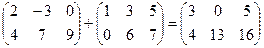 .
.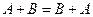 ;
;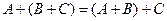
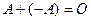 ;
;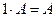 ;
;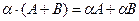 ;
; ;
;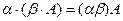 ;
;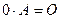 .
.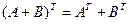 .
.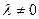 ;
; Две матрицы
Две матрицы 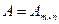 и
и 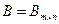 - эквивалентные, если одна из них получается из другой при помощи элементарных преобразований. Пишут А ~ В. При помощи элементарных преобразований матрицу
- эквивалентные, если одна из них получается из другой при помощи элементарных преобразований. Пишут А ~ В. При помощи элементарных преобразований матрицу 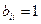 ,
, 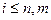 , а
, а 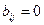 ,
, 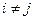 . Например:
. Например: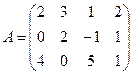 ~
~ 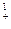
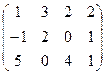 ~
~ 
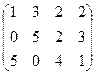 ~
~ 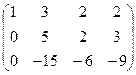 ~
~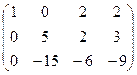 ~
~ 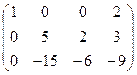 ~
~ 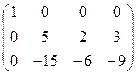 ~
~ 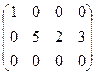 ~
~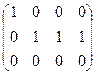 ~
~ 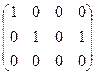 ~
~ 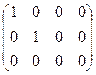 = B.
= B.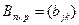 , то определяется произведение этих матриц
, то определяется произведение этих матриц 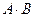 , при котором получается матрица
, при котором получается матрица 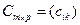 такая, что
такая, что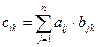
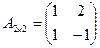 и
и 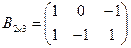 .
.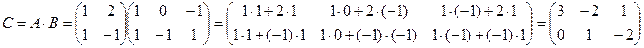
 не существует, так как
не существует, так как  , где 3 - число столбцов для матрицы В, а 2 - число строк для А.
, где 3 - число столбцов для матрицы В, а 2 - число строк для А. , то существуют матрицы
, то существуют матрицы 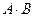 и
и 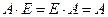 . В общем случае
. В общем случае 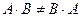 . Например, если
. Например, если  ,
, 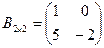 , то
, то 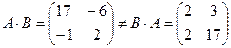 .
.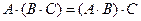 ;
;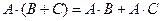 ;
;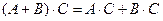 ;
;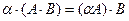 .
.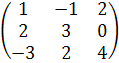 В =
В = 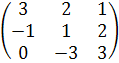
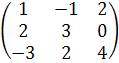 ∙
∙ 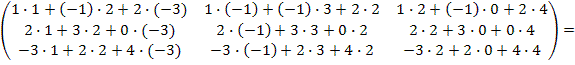
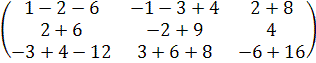 =
= 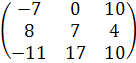
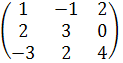 ∙
∙ 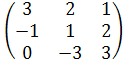 =
=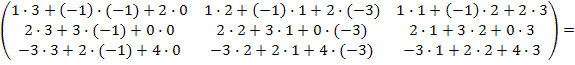
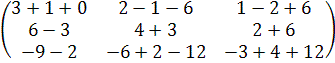 =
= 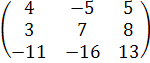
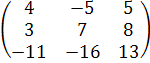 =(чтобы умножить матрицу на число надо каждый элемент матрицы умножить на это число)=
=(чтобы умножить матрицу на число надо каждый элемент матрицы умножить на это число)= 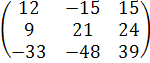 .
. -
- 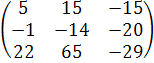 .
.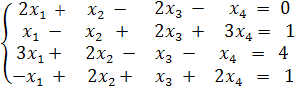 (1)
(1)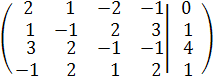

 С 2 С 1,здесь С 2 – вторая строка, С 1 – первая строка, при этом получим эквивалентную матрицу
С 2 С 1,здесь С 2 – вторая строка, С 1 – первая строка, при этом получим эквивалентную матрицу
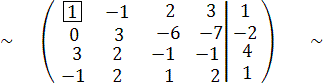
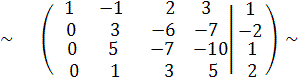

 С 4 С 2,
С 4 С 2,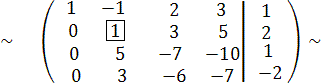
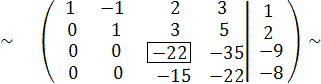
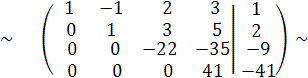
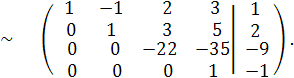
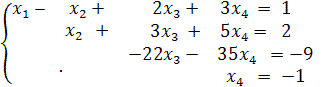
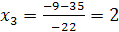
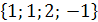 .
.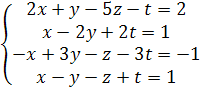 .
.
 A =
A = 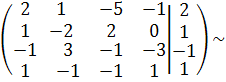 С 2 С 1
С 2 С 1 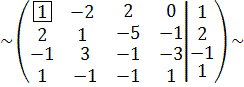

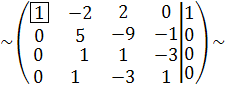
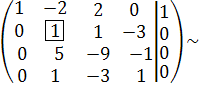
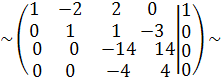
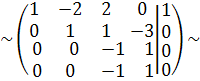 С 4:= - С 3 + С 4
С 4:= - С 3 + С 4 
 . Тогда находим общее решение системы.Для этого составим по полученной матрице систему уравнений
. Тогда находим общее решение системы.Для этого составим по полученной матрице систему уравнений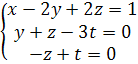 =>
=> 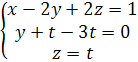 =>
=> 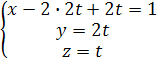
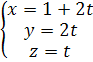 .
.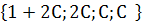 ,где С-параметр решения.
,где С-параметр решения.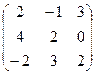 и В =
и В = 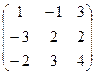 .
.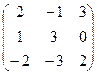 и В =
и В = 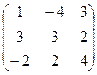 .
.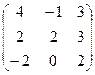 и В =
и В = 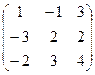 .
.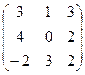 и В =
и В =  .
.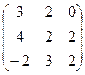 и В =
и В = 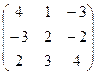 .
.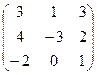 и В =
и В = 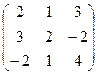 .
.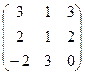 и В =
и В = 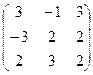 .
.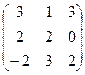 и В =
и В = 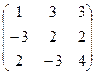 .
.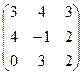 и В =
и В = 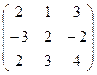 .
.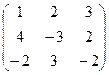 и В =
и В = 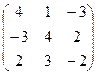 .
.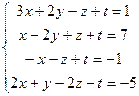 6.
6. 
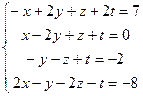 7.
7. 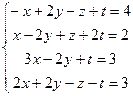
 8.
8. 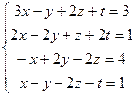
 9.
9. 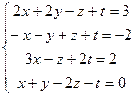
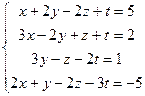 10.
10. 
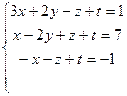 2.
2. 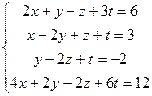
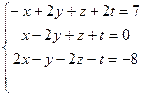 4.
4. 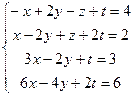
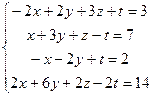 6.
6. 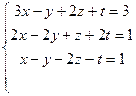
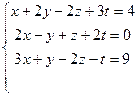 8.
8. 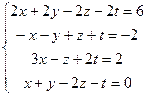
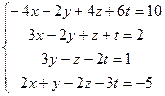 10.
10. 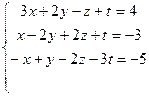
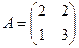 2.
2. 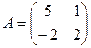
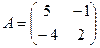 4.
4. 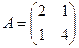
 6.
6. 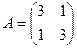
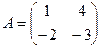 8.
8. 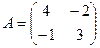
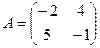 10.
10. 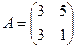
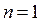 .
. 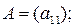
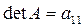 ;
;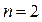 .
.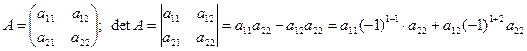 ;
;
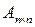 , то det A находится с помощью разложения Лапласа:
, то det A находится с помощью разложения Лапласа: 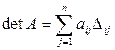
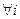 ,
, 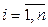 , где Aij =
, где Aij = 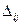 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 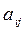 , т.е.
, т.е.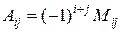 ,
,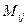 - минор элемента
- минор элемента 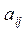 , т.е. определитель квадратной матрицы А, полученный из А вычеркиванием i -ой строки и j -ого столбца.
, т.е. определитель квадратной матрицы А, полученный из А вычеркиванием i -ой строки и j -ого столбца.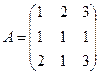
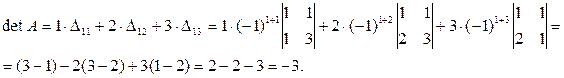
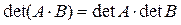 (использовать правило Лапласа) и что
(использовать правило Лапласа) и что 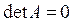 Û если имеются в А нулевая строка или нулевой столбец или две пропорциональные строки или столбца.
Û если имеются в А нулевая строка или нулевой столбец или две пропорциональные строки или столбца.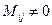 матрицы An ‰ n называется ее рангом и обозначается r,
матрицы An ‰ n называется ее рангом и обозначается r,  или rang A. Очевидно, что
или rang A. Очевидно, что 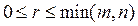 . Минор, порядок которого определяет ранг матрицы, называется базисным. Ранг матрицы А равен числу единиц на главной диагонали канонической матрицы, к которой приводится матрица А путем элементарных преобразований. Например,
. Минор, порядок которого определяет ранг матрицы, называется базисным. Ранг матрицы А равен числу единиц на главной диагонали канонической матрицы, к которой приводится матрица А путем элементарных преобразований. Например,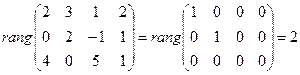 .
.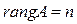 , т.е. базисный минор совпадает с определителем матрицы
, т.е. базисный минор совпадает с определителем матрицы 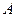 . В противном случае, когда rang А < n, A называется вырожденной матрицей. В этом случае
. В противном случае, когда rang А < n, A называется вырожденной матрицей. В этом случае 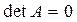 .
.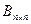 , удовлетворяющая условиям
, удовлетворяющая условиям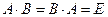 ,
,


