

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
Обыкновенные дифференциальные уравнения.
Задачи, приводящие к дифференциальным уравнениям (ДУ). ДУ 1-го порядка. Частные и общее решения ДУ, интегральные кривые. Задача Коши и теорема существования и единственности ее решения. Особые точки и особые решения ДУ.

Рис. 30
Рассмотрим на плоскости семейство эллипсов

 – произвольная положительная постоянная (см. рис. 30).
– произвольная положительная постоянная (см. рис. 30).
Найдем семейство кривых, ортогональных семейству эллипсов.
1. Составим дифференциальное уравнение (ДУ) семейства эллипсов.
Продифференцируем уравнение (2.1.1), считая 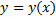 :
:

Отсюда  - ДУ семейства эллипсов. Тогда
- ДУ семейства эллипсов. Тогда  =
= 
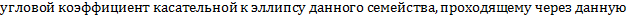

2. Составим ДУ ортогонального семейства. В т. 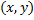 угловой коэффициент касательной должен быть равен
угловой коэффициент касательной должен быть равен  , т.е. ДУ ортогонального семейства:
, т.е. ДУ ортогонального семейства:
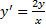 .
.
3. Найдем уравнение ортогонального семейства:

Получаем  – семейство парабол.
– семейство парабол.
Обыкновенное ДУ 1-го порядка -
 , где
, где  – неизвестная функция;
– неизвестная функция;  – функция 3-х переменных.
– функция 3-х переменных.
ДУ 1-го порядка, разрешенные относительно производной:

 – определена в области
– определена в области  .
.
Опр. Частным решением ДУ (2.1.2) называется функция  , определенная на
, определенная на 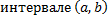 , при подстановке которой в ДУ (2.1.2) оно обращается в тождество на
, при подстановке которой в ДУ (2.1.2) оно обращается в тождество на  , т.е.
, т.е.  .
.
Пример.
 .
.
 – частное решение, т.к.
– частное решение, т.к.  – тождество;
– тождество;
 – также частное решение, т.к.
– также частное решение, т.к.  – тождество.
– тождество.
Опр. График частного решения 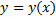 ДУ
ДУ 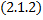 называется интегральной кривой ДУ
называется интегральной кривой ДУ 
Опр. Равенство 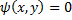 , неявно задающее решение ДУ
, неявно задающее решение ДУ  называется частным интегралом ДУ
называется частным интегралом ДУ 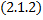 .
.
Задача Коши для ДУ  : найти частные решения ДУ
: найти частные решения ДУ 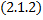 , удовлетворяющие начальному условию
, удовлетворяющие начальному условию  , где
, где 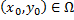 ,
,
т.е. задача Коши может быть записана следующими образом:

Геометрический смысл: найти интегральную кривую ДУ 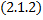 , проходящую через т.
, проходящую через т.  .
.
Теорема Коши существования и единственности решения задачи Коши для ДУ 1-го порядка.
Пусть функция  и ее частная производная
и ее частная производная  непрерывны в области
непрерывны в области  . Тогда для
. Тогда для  точки
точки  существует и при том единственное решение задачи Коши.
существует и при том единственное решение задачи Коши.
Геометрический смысл:  единственная интегральная кривая, проходящая через т.
единственная интегральная кривая, проходящая через т.  .
.
Замечание. Решение определено только в  окрестности т.
окрестности т.  .
.
Пример.

 и
и  непрерывны в области
непрерывны в области 




 , т.е. в окрестности точки 0. В любой большей окрестности 0 функция
, т.е. в окрестности точки 0. В любой большей окрестности 0 функция 
 и не удовлетворяет ДУ в этих точках.
и не удовлетворяет ДУ в этих точках.
Пример (неединственность в задаче Коши).
 ,
,



Из начального условия  .
.
 – также решение данной задачи Коши.
– также решение данной задачи Коши.
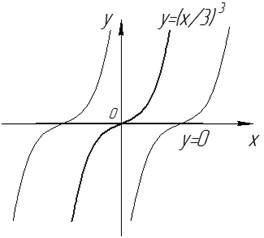
Рис. 31
Через точку 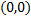 проходит более одной интегральной кривой (см. рис. 31). Не выполняется условие непрерывности
проходит более одной интегральной кривой (см. рис. 31). Не выполняется условие непрерывности 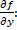


Опр. Общим решением ДУ 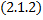 называется семейство функций, зависящих от параметра
называется семейство функций, зависящих от параметра  , т.е.
, т.е.  ,
,  – произвольная постоянная, такое, что:
– произвольная постоянная, такое, что:
1. для  фиксированного
фиксированного  функция
функция  является частным решением,
является частным решением,
2. для  т.
т.  такое, что частное решение
такое, что частное решение  удовлетворяет начальному условию
удовлетворяет начальному условию 
Замечание. ДУ  можно записать в виде
можно записать в виде  (используя то, что
(используя то, что  .
.
Опр. Равенство  , неявно задающее общее решение называется общим интегралом ДУ
, неявно задающее общее решение называется общим интегралом ДУ 
Обыкновенные дифференциальные уравнения.
Задачи, приводящие к дифференциальным уравнениям (ДУ). ДУ 1-го порядка. Частные и общее решения ДУ, интегральные кривые. Задача Коши и теорема существования и единственности ее решения. Особые точки и особые решения ДУ.

Рис. 30
Рассмотрим на плоскости семейство эллипсов

 – произвольная положительная постоянная (см. рис. 30).
– произвольная положительная постоянная (см. рис. 30).
Найдем семейство кривых, ортогональных семейству эллипсов.
1. Составим дифференциальное уравнение (ДУ) семейства эллипсов.
Продифференцируем уравнение (2.1.1), считая 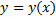 :
:

Отсюда  - ДУ семейства эллипсов. Тогда
- ДУ семейства эллипсов. Тогда  =
= 
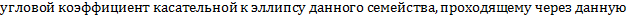

2. Составим ДУ ортогонального семейства. В т. 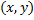 угловой коэффициент касательной должен быть равен
угловой коэффициент касательной должен быть равен  , т.е. ДУ ортогонального семейства:
, т.е. ДУ ортогонального семейства:
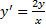 .
.
3. Найдем уравнение ортогонального семейства:

Получаем  – семейство парабол.
– семейство парабол.
Обыкновенное ДУ 1-го порядка -
 , где
, где  – неизвестная функция;
– неизвестная функция;  – функция 3-х переменных.
– функция 3-х переменных.
ДУ 1-го порядка, разрешенные относительно производной:

 – определена в области
– определена в области  .
.
Опр. Частным решением ДУ (2.1.2) называется функция  , определенная на
, определенная на 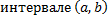 , при подстановке которой в ДУ (2.1.2) оно обращается в тождество на
, при подстановке которой в ДУ (2.1.2) оно обращается в тождество на  , т.е.
, т.е.  .
.
Пример.
 .
.
 – частное решение, т.к.
– частное решение, т.к.  – тождество;
– тождество;
 – также частное решение, т.к.
– также частное решение, т.к.  – тождество.
– тождество.
Опр. График частного решения 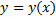 ДУ
ДУ 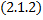 называется интегральной кривой ДУ
называется интегральной кривой ДУ 
Опр. Равенство 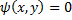 , неявно задающее решение ДУ
, неявно задающее решение ДУ  называется частным интегралом ДУ
называется частным интегралом ДУ 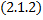 .
.
Задача Коши для ДУ  : найти частные решения ДУ
: найти частные решения ДУ 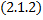 , удовлетворяющие начальному условию
, удовлетворяющие начальному условию  , где
, где 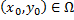 ,
,
т.е. задача Коши может быть записана следующими образом:

Геометрический смысл: найти интегральную кривую ДУ 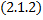 , проходящую через т.
, проходящую через т.  .
.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!