Графический метод решения задач нелинейного программирования

 

В задаче нелинейного программирования в общей ее постановке система ограничений определяет в n – мерном пространстве некоторую область, которая является областью допустимых решений задачи. Аналогично задачам ли­нейного программирования, задачи нелинейного программирования можно решать гра­фически, когда целевая функция и система ограничений содержат только две управляющие переменные, а ограничения представляют собой неравенства.

Решить задачу нелинейного программирования графически – значит найти точку области допустимых решений, через которую проходит линия наиболь­шего (наименьшего) уровня целевой функции: . Причем, в отличие от задачи линейного программи­рования, указанная точка может находиться как на границе, так и внутри области допустимых решений.

Алгоритм решения задачи нелинейного программирования графическим методом состоит из следующих основных шагов.

Шаг 1. На плоскости  строят область допустимых реше­ний, опреде­ляемую ограничениями. Если она пуста, т.е. если ограни­чения несовместны, то задача не имеет решений. В противном случае переходят к шагу 2.

Шаг 2. Строят линию уровня целевой функции: , где C – неко­торая константа. Переходят к шагу 3.

Шаг 3. Определяют направление возрастания (при задаче на максимум) или убывания (при задаче на минимум) целевой функции посредством вычисле­ния координат и построения вектора градиента целевой функции.

Шаг 4. Находят точку области допустимых решений, через которую про­ходит линия уровня целевой функции с наибольшим (при решении задач на мак­симум), или наименьшим (при решении задач на минимум) значением конс­танты C, или устанавливают неограни­ченность целевой функции на области до­пустимых решений.

Шаг 5. Определяют значения координат 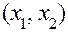 для точки, найденной на шаге 4, а также значение целевой функции в этой точке, т.е. при найденных зна­чениях координат этой точки.

 

ПРИМЕР: Найдите графическим методом оптимальные решения задачи нелинейного программирования, заданной математической моделью вида:

 

В соответствии с алгоритмом построим на плоскости  об­ласть допустимых решений. Ограничения 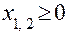 выделяют первую чет­верть. Границей полуплоскости по первому ограничению является гипербола с уравнением: , причем неравенство ограничения выполняется для точек, лежащих выше этой гиперболы. Второй границей является окружность, точнее ее четвер­тая часть в первой четверти, с радиусом 3 и центром в начале координат. На рис. 5 область допустимых решений задачи выделена штрихов­кой.

Очевидно, что вектор градиента целевой функции определяется координа­тами:   и, следовательно, направлен вправо вверх, как указано стрел­кой. Как известно, целевая функция возрастает в направлении вектора гра­диента и убывает в направлении вектора антиградиента, и, кроме того, любая линия уровня целевой функции перпендикулярна этому вектору. Поэтому мак­симум целевой функции достигается в точке В, а минимум – в точке А. И задача сводится к нахождению координат этих точек.

Рис. 5.

Заметим, что в точке В совпадают тангенсы углов наклона касательной к окружности и прямой – линии уровня целевой функции к оси 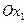, а также, что эти тангенсы численно равны производным этих функций (вычисленным в точке В). Для линии уровня угловой коэффициент (тангенс угла наклона) очевидно равен: , а для окружности угловой коэффициент касательной равен: , поэтому можно записать уравнение: . Если к этому уравнению добавить уравнение окружности, то получится система уравнений вида:

 

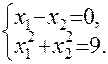
Решения системы  и являются координатами точки В, и, следовательно, являются оптимальными решениями задачи на максимум целевой функции, при этом: .

Для минимума целевой функции, аналогично в точке А имеем:  для прямой – линии уровня целевой функции и  для касательной к гиперболе. Приравнивая найденные выражения, получим:  и подставив найденное значение в уравнение гиперболы, получим: . Поэтому оптимальное решение для задачи на минимум целевой функции будет иметь следующий вид: .

Метод множителей Лагранжа

 

Пусть требуется решить задачу нелинейного программирования, заданную математической моделью в каноническом виде:

 

 

Причем в этой модели функции  и  непрерывны вместе со своими частными производными по всем управляющим переменным: .

Для решения поставленной задачи может быть применен метод множите­лей Лагранжа, пошаговый алгоритм которого состоит в следующем.

Шаг 1. Составляют функцию Лагранжа:

 

,

где переменные  называются множителями Лагранжа.

Шаг 2. Находят частные производные функции Лагранжа по всем перемен­ным и приравнивают их к нулю:

 

 

Шаг 3. Решают систему уравнений, полученную на шаге 2, и находят ста­ционарные точки, т.е. точки, в которых функция F (и, следовательно, исходя из структуры функции F, целевая функция f) может иметь экстремум.

Шаг 4. Проверяют полученные на шаге 3 стационарные точки на наличие в них экстремума и находят экстремальное значение целевой функ­ции задачи в найденной точке условного (в смысле не глобального) экстрему­ма.

 

ПРИМЕР: Фирма реализует автомобили двумя способами: через магазин и через торговых агентов. При реализации  автомобилей через магазин расходы на реализацию составляют:  условных единиц, а при продаже  автомобилей через торговых агентов расходы составляют 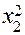 условных единиц. Найти оптимальный способ реа­лизации автомобилей, обеспечивающий минимум суммарных расходов, если общее число автомобилей, предназначенных для продажи, составляет 200 штук.

 

Очевидно, что математическая модель задачи будет иметь вид:

 

 

Анализ модели показывает, что налицо задача нелинейного программиро­вания с нелинейной целевой функцией и линейным ограничением. Для расчета модели, т.е. для решения задачи, приме­ним метод множителей Лагранжа.

В рассматриваемом случае функция Лагранжа будет иметь вид:

 

.

 

Вычислив частные производные и приравняв их нулю, полу­­чим следующую систему уравнений:

 

 

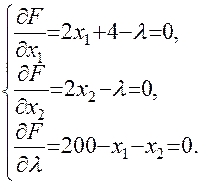
Решив эту систему, получим:  и . Этим зна­че­ниям управляющих переменных соответствует значение целевой функции, равное: .

Для того чтобы убедиться в том, что найденные значения управляющих переменных действительно доставляют минимум целевой функции, вычислим значения вторых частных производных функции F в стационарной точке и сос­тавим определитель:

 

.

 

Поскольку найденный определитель больше нуля, в найденной ста­ционарной точке есть экстремум, а т.к. , то это минимум. Следова­тельно, в этой точке целевая функция задачи имеет условный минимум.

Таким образом, для получения минимальных расходов на реализацию, фирме следует реализовать 99 автомобилей через магазин и 101 автомобиль че­рез торговых агентов. При этом расходы на реализацию составят 20398 условных единиц.

 

При решении задач нелинейного программирования методом множителей Лагранжа значения этих множителей не вычисляют, а при решении соответствующей системы уравнений выражают их через управляющие переменные, т.е. исключают.

Рекомендуемая литература по теме 4: [1 ÷ 4].

 

ВОПРОСЫ для самопроверки знаний по теме 4:

1. Для решения каких экономических задач чаще всего приме­няются нелиней­ные математические модели?

 

 

 

 

2. При каких условиях задача нелинейного программирования может быть решена графическим методом?

 

 

 

 

3. В каком виде должна быть записана математическая модель задачи нелинейного программирования для решения ее методом множителей Лагранжа?

 

 

 

 

4. В чем заключается основная идея метода множителей Лагранжа?