1. Каждому 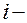 му неравенству системы ограничений исходной задачи ставится в соответствие переменная
му неравенству системы ограничений исходной задачи ставится в соответствие переменная  .
.
2. Составляют целевую функцию, коэффициентами которой будут свободные члены системы ограничений исходной задачи, т.е. величины  .
.
3. Составляют систему ограничений по правилу: коэффициенты новой системы ограничений образуют транспонированную матрицу коэффициентов исходной системы ограничений; при этом знаки неравенств изменяют на противоположные.
4. Свободными членами новой системы ограничений будут коэффициенты целевой функции исходной задачи.
5. Все переменные двойственной задачи не отрицательны, а направление оптимизации новой целевой функции противоположно направлению оптимизации целевой функции исходной задачи.
Реализовав перечисленные в правилах действия, получим математическую модель двойственной задачи в виде:

Если модель исходной задачи имеет канонический вид, то при составлении математической модели двойственной задачи используют все правила, приведенные выше, с добавлением еще одного правила:
6. Ограничениями двойственной задачи будут неравенства, причем, если в целевой функции составляемой двойственной задачи требуется найти минимум, то ставится знак неравенства «больше или равно», если же – максимум, то знак «меньше или равно».
Замечание. При построении математической модели смешанной двойственной задачи, т.е. когда модель исходной задачи содержит как условия симметричной задачи, так и несимметричной, необходимо выполнять все правила, указанные выше.
Для оптимальных решений задач линейного программирования, образующих двойственную пару справедливы следующие теоремы двойственности.
Теорема 1. Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений  и
и  выполняется равенство:
выполняется равенство:  .
.
Если же одна из двойственных задач не имеет решения, ввиду того, что:  , или:
, или:  , то другая задача не имеет допустимых решений.
, то другая задача не имеет допустимых решений.
Теорема 2. Для оптимальности допустимых решений  и
и  пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений:
пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений:

Практическая сущность теоремы 2 состоит в следующем: если при подстановке оптимального решения в систему ограничений i -ое ограничение исходной задачи выполняется как строгое неравенство, то i -ая компонента оптимального решения двойственной задачи равна нулю, и, наоборот, если i -ая компонента оптимального решения двойственной задачи положительна, то i -ое ограничение исходной задачи удовлетворяется оптимальным решением как равенство.
Обе сформулированные теоремы позволяют определить оптимальное решение одной из задач двойственной пары по оптимальному решению другой.
ПРИМЕР: Математическая модель задачи линейного программирования имеет вид:

Составьте математическую модель двойственной задачи и по оптимальному решению одной из задач найдите оптимальное решение другой.
Применив приведенные правила, получим математическую модель двойственной задачи в виде:
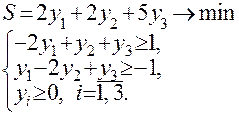
Если решить исходную задачу графическим методом, то получим:  и при этом:
и при этом:  . На основании первой теоремы двойственности заключаем, что:
. На основании первой теоремы двойственности заключаем, что:  . Поскольку полученные оптимальные решения исходной задачи положительны, по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств или уравнений:
. Поскольку полученные оптимальные решения исходной задачи положительны, по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств или уравнений:

Теперь подставим значения  и
и  в систему ограничений исходной задачи и получим:
в систему ограничений исходной задачи и получим:

На этом основании система ограничений двойственной задачи примет вид:

Решая ее, окончательно находим:  и при этом:
и при этом:  .
.
Теперь решим обратную задачу. Пусть дано оптимальное решение двойственной задачи: 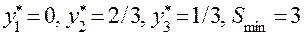 . По первой теореме двойственности имеем:
. По первой теореме двойственности имеем:  . Так как
. Так как  , то по второй теореме двойственности заключаем, что второе и третье неравенства исходной задачи обращаются в равенства, или в уравнения:
, то по второй теореме двойственности заключаем, что второе и третье неравенства исходной задачи обращаются в равенства, или в уравнения:

Решив эту систему, находим:  и при этом:
и при этом:  .
.
Тема 2. Транспортная задача





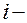 му неравенству системы ограничений исходной задачи ставится в соответствие переменная
му неравенству системы ограничений исходной задачи ставится в соответствие переменная  .
. .
.
 и
и  выполняется равенство:
выполняется равенство:  .
. , или:
, или:  , то другая задача не имеет допустимых решений.
, то другая задача не имеет допустимых решений. и
и  пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений:
пары двойственных задач необходимо и достаточно, чтобы они удовлетворяли системе уравнений:

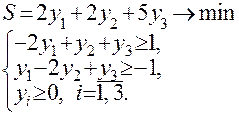
 и при этом:
и при этом:  . На основании первой теоремы двойственности заключаем, что:
. На основании первой теоремы двойственности заключаем, что:  . Поскольку полученные оптимальные решения исходной задачи положительны, по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств или уравнений:
. Поскольку полученные оптимальные решения исходной задачи положительны, по второй теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств или уравнений:
 и
и  в систему ограничений исходной задачи и получим:
в систему ограничений исходной задачи и получим:

 и при этом:
и при этом:  .
.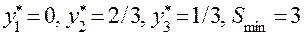 . По первой теореме двойственности имеем:
. По первой теореме двойственности имеем:  . Так как
. Так как  , то по второй теореме двойственности заключаем, что второе и третье неравенства исходной задачи обращаются в равенства, или в уравнения:
, то по второй теореме двойственности заключаем, что второе и третье неравенства исходной задачи обращаются в равенства, или в уравнения:
 и при этом:
и при этом:  .
.


