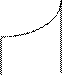
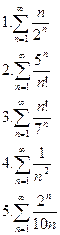Опр.6.1. Фигура, ограниченная снизу отрезком 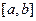 оси ох, сверху
оси ох, сверху
графиком функции 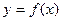 , с боков отрезками х=а, х= b,
, с боков отрезками х=а, х= b,
 называется криволинейной трапецией.
называется криволинейной трапецией.
Площадь криволинейной трапеции вычисляется по формуле:
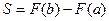
Таким образом, вычисление площади криволинейной трапеции сводится к отысканию первообразной F(x) функции 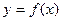 , т.е. к интегрированию F(x).
, т.е. к интегрированию F(x).
Опр. 6.2. Разность 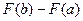 называется интегралом от функции F(x) и обозначается
называется интегралом от функции F(x) и обозначается 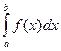 .
.
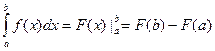 - формула Ньютона – Лейбница.
- формула Ньютона – Лейбница.
Пример. Найти площадь фигуры, ограниченной графиком 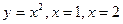




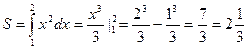
Свойства определенного интеграла аналогичны свойствам неопределенного интеграла.
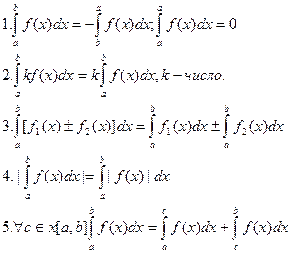
Задание 1. Вычислить площадь фигуры, ограниченной
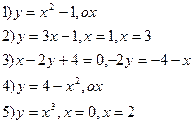
Задача 2. Вычислить определенный интеграл.
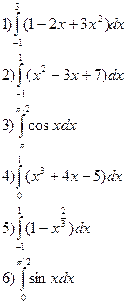
Метод замены переменной (метод подстановки).
Существует три метода вычисления интегралов: непосредственное интегрирование, метод замены переменной, метод интегрирования по частям.
Пример.
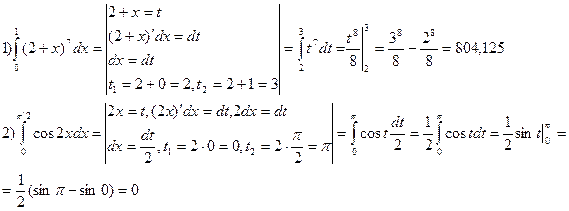
Задачи.
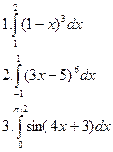
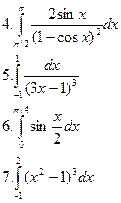
Самостоятельная работа №1.
Дифференциальные уравнения.
Опр.8.1. Диф.уравнением называется уравнение, связывающее функцию 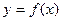 , переменную x и производную f(x).
, переменную x и производную f(x).
Опр. 8.2. Если функция 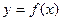 зависит только от переменной x, то диф.урав. называется обыкновенным.
зависит только от переменной x, то диф.урав. называется обыкновенным.
Общий вид обыкновенного диф.уравнения. 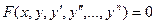 .
.
Опр. 8.3. Максимальный порядок входящих в уравнение производных называется порядком диф.уравнения.
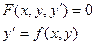 -диф.уравнение первого порядка.
-диф.уравнение первого порядка.
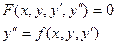 - диф. Уравнение второго порядка.
- диф. Уравнение второго порядка.
Решить диф.уравнение – значит найти первообразную функции f(x), т.е. вычислить неопределенный интеграл от F(x).
Пусть дано диф.ур. первого порядка 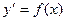 , необходимо его решить.
, необходимо его решить.
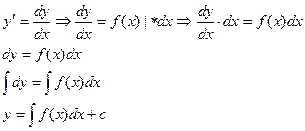 общее решение диф.уравнения.
общее решение диф.уравнения.
Алгоритм решения диф.уравнений:
1. 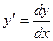
2. домножаем обе части уравнения на 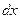 и переносим слагаемые с
и переносим слагаемые с 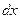 в другую сторону.
в другую сторону.
3. Переменные, содержащие x переносим к 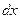 , а переменные, содержащие y к
, а переменные, содержащие y к 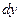 .
.
4. Интегрируем обе части уравнения.
Пример. Решить диф.уравнение.
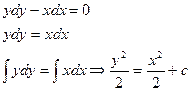
Уравнению вида 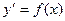 можно придать вид
можно придать вид
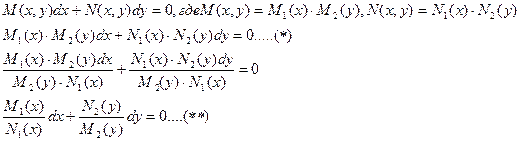
Опр.8.4. Уравнение (*) называется уравнением с разделяющимися переменными, а уравнение (**) – уравнением с разделенными переменными.
Пример. 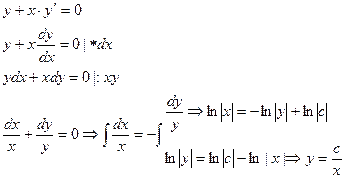
Однородные дифференциальные уравнения первого порядка.
Опр. 9.1. Функция 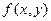 называется однородной, если
называется однородной, если 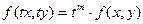
Пример. 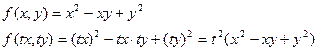
Опр. 9.2. Уравнение вида 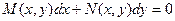 называется однородным дифференциальным уравнением первого порядка.
называется однородным дифференциальным уравнением первого порядка.
Опр. 9.3. Уравнение 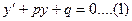 называется линейным дифференциальным уравнением первого порядка.
называется линейным дифференциальным уравнением первого порядка.
Такое уравнение вычисляется с помощью замены 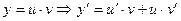 подставим в (1) =>
подставим в (1) =>
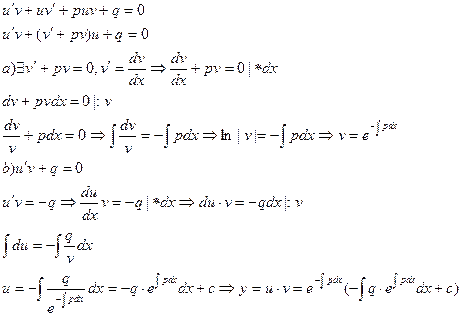
Задача. Решить диф.уравнение.
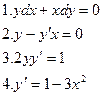
5. 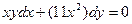 9.
9. 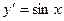
6. 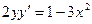 10.
10. 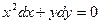
7. 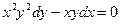 11.
11. 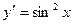
8. 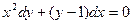 12.
12. 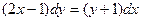
13. 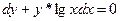
Частные производные
Дана функция двух переменных Z=F(x,y),дадим аргументу x приращение Bx, а арг. Y менять не будем, Т.Е. перейдем от точки с координатами (x,y) к точке с координатоми (x+bx,y).
Тогда функция F(x,y) получит приращение 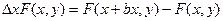 ,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
Опр.10.1: 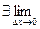
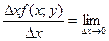
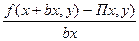
Он над частной производной ф-ии
F(x,y) и обозн. 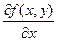
Аналогична опред-ся ч.пр. F(x,y) по Y
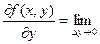
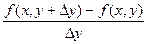
Т.Е ч.пр. 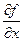 это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр
это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр 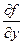 это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
Пр; Найти ч.пр. ф-ии 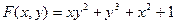
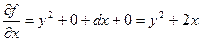
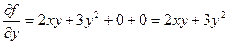
Задачи:
1. 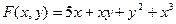 6.
6. 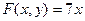
2. 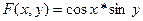 7.
7. 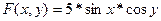
3. 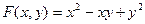 8.
8. 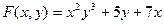
4. 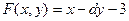 9.
9. 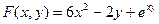
5. 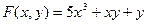 10.
10. 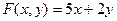
Глава 2. Ряды.
Числовые ряды.
Ряды бывают: числовые, функциональные, степенные, конечные и бесконечные, знакопеременные.
Опр.1.1. Числовым рядом называется выражение вида 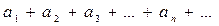 , где
, где 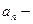 числа.
числа.
Для сокращенного обозначения рядов используют знак 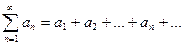
Пример. 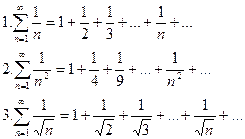
Опр. 1.2. Сумма первых n элементов ряда называется частичной суммой ряда 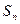 .
.
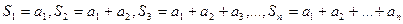
Опр. 1.3. Ряд называется сходящимся, если последовательность его частичных сумм сходится, т.е. 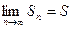 , где S – сумма ряда. (если предел не существует или равен
, где S – сумма ряда. (если предел не существует или равен 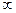 , то ряд расходится).
, то ряд расходится).
Пример. Определить сходимость ряда 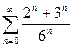 - геометрическая прогрессия.
- геометрическая прогрессия.
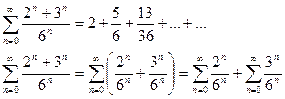
Докажем сходимость каждого ряда.
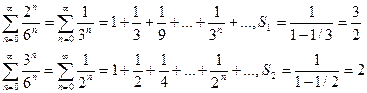
Эти ряды являются рядами бесконечной геометрической прогрессии со знаменателем <1, тогда 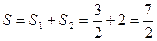 . Так как сумма ряда конечное число, то ряд сходится.
. Так как сумма ряда конечное число, то ряд сходится.
Т. 1.1. (Необходимый признак сходимости рядов).
Если ряд сходится, то его общий элемент стремится к нулю, т.е. 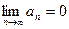 .
.
Пример. 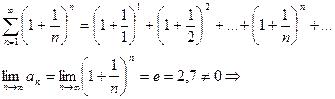 ряд расходится.
ряд расходится.
Признак Даламбера сходимости рядов.
Пусть дан ряд 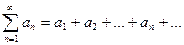 Допустим, что
Допустим, что 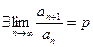 , тогда
, тогда
1) Если p<1, то ряд сходится.
2) Если p>1, то ряд расходится.
Пример. 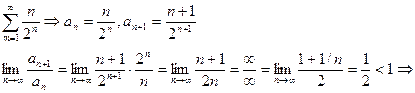 ряд сходится.
ряд сходится.
Задача. Написать первые пять элементов ряда по заданному общему элементу и проверить сходится ли ряд.
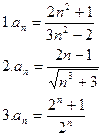
Знакопеременные ряды.
Опр.2.1. Рассмотрим ряд, у которого все элементы по очереди меняют знак: 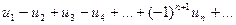 , где
, где 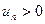 . Такой ряд называется знакочередующимся.
. Такой ряд называется знакочередующимся.
Пример. 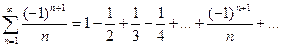
Т.2.1. (Признак Лейбница).
Пусть знакочередующийся ряд удовлетворяет следующим условиям:
- Все элементы ряда убывают
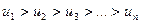 .
. - Общий элемент ряда стремится к 0 при
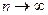 .
.
Тогда ряд сходится.
Функциональные ряды.
Опр. 3.1. Пусть дана бесконечная последовательность функций 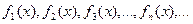 , где все функции определены на некотором множестве, тогда ряд
, где все функции определены на некотором множестве, тогда ряд 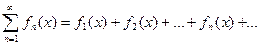 называется функциональным рядом.
называется функциональным рядом.
Если вместо аргумента x поставить конкретное число, то получим числовой ряд 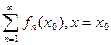 .
.
Опр. 3.2. Если этот ряд сходится, то точка 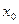 называется точкой сходимости ряда.
называется точкой сходимости ряда.
Опр. 3.3. совокупность всех точек сходимости ряда называется областью сходимости ряда.
Факториал! n!=1*2*3*4*…*n
3!=1*2*3
2!=1*2
1!=1
0!=1
Пример. 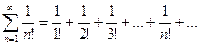
Определить сходимость данного ряда по признаку Даламбера.
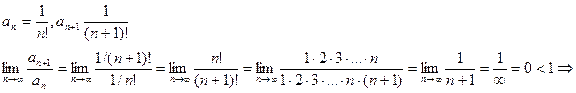 ряд сходится.
ряд сходится.
Задача. Определить сходимость ряда.
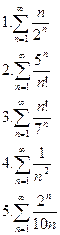
Контрольная работа по трем темам: производная, ряды, диф.уравнения.



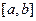 оси ох, сверху
оси ох, сверху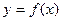 , с боков отрезками х=а, х= b,
, с боков отрезками х=а, х= b,
 называется криволинейной трапецией.
называется криволинейной трапецией.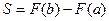
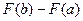 называется интегралом от функции F(x) и обозначается
называется интегралом от функции F(x) и обозначается 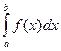 .
.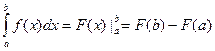 - формула Ньютона – Лейбница.
- формула Ньютона – Лейбница.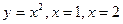




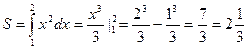
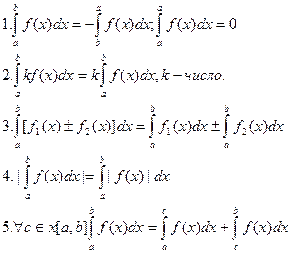
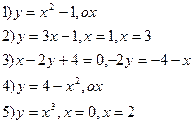
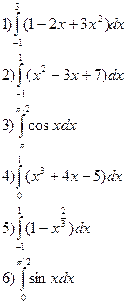
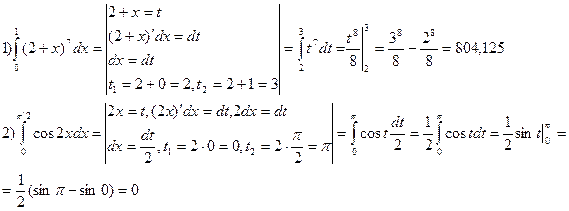
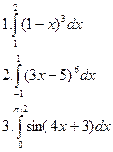
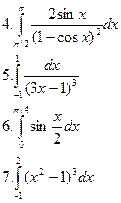
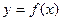 зависит только от переменной x, то диф.урав. называется обыкновенным.
зависит только от переменной x, то диф.урав. называется обыкновенным.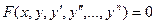 .
.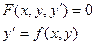 -диф.уравнение первого порядка.
-диф.уравнение первого порядка.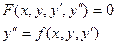 - диф. Уравнение второго порядка.
- диф. Уравнение второго порядка.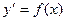 , необходимо его решить.
, необходимо его решить.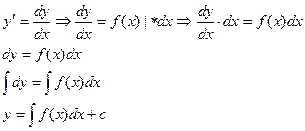 общее решение диф.уравнения.
общее решение диф.уравнения.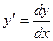
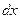 и переносим слагаемые с
и переносим слагаемые с 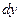 .
.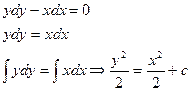
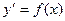 можно придать вид
можно придать вид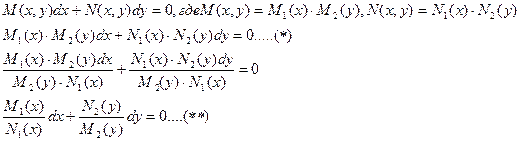
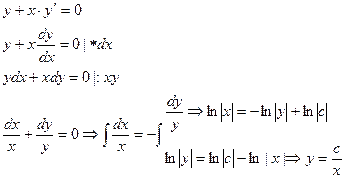
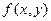 называется однородной, если
называется однородной, если 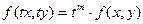
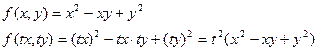
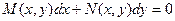 называется однородным дифференциальным уравнением первого порядка.
называется однородным дифференциальным уравнением первого порядка.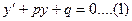 называется линейным дифференциальным уравнением первого порядка.
называется линейным дифференциальным уравнением первого порядка.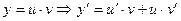 подставим в (1) =>
подставим в (1) =>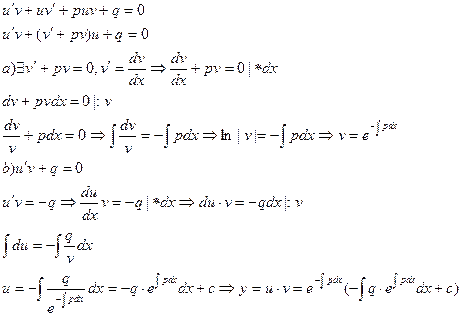
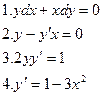
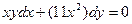 9.
9. 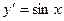
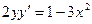 10.
10. 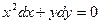
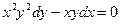 11.
11. 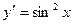
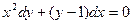 12.
12. 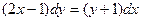
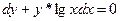
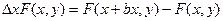 ,которое над частным приращ. Ф-ии. F(x,y) по переменой x.
,которое над частным приращ. Ф-ии. F(x,y) по переменой x.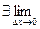
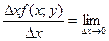
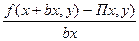
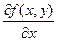
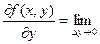
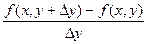
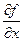 это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр
это обычная производная ф. F(x,y) по переменой x при фиксиров.знач. y, а ч.пр 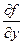 это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X
это есть обыч. Пр. Ф. F(x,y) по переменой y при фиксир. Знач. X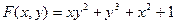
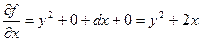
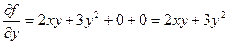
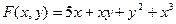 6.
6. 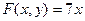
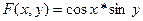 7.
7. 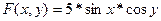
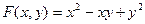 8.
8. 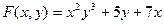
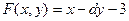 9.
9. 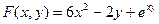
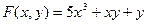 10.
10. 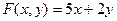
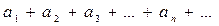 , где
, где 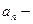 числа.
числа.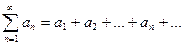
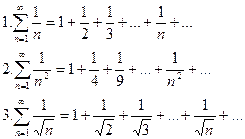
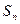 .
.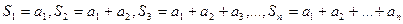
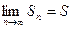 , где S – сумма ряда. (если предел не существует или равен
, где S – сумма ряда. (если предел не существует или равен 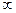 , то ряд расходится).
, то ряд расходится).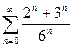 - геометрическая прогрессия.
- геометрическая прогрессия.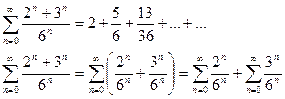
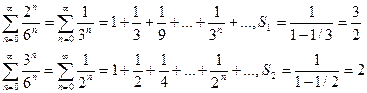
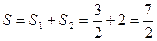 . Так как сумма ряда конечное число, то ряд сходится.
. Так как сумма ряда конечное число, то ряд сходится.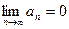 .
.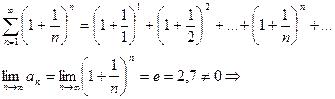 ряд расходится.
ряд расходится.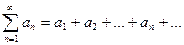 Допустим, что
Допустим, что 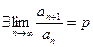 , тогда
, тогда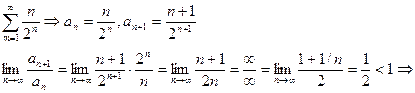 ряд сходится.
ряд сходится.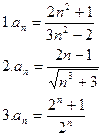
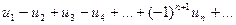 , где
, где 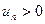 . Такой ряд называется знакочередующимся.
. Такой ряд называется знакочередующимся.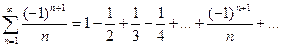
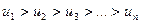 .
.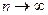 .
.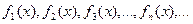 , где все функции определены на некотором множестве, тогда ряд
, где все функции определены на некотором множестве, тогда ряд 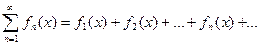 называется функциональным рядом.
называется функциональным рядом.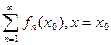 .
.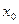 называется точкой сходимости ряда.
называется точкой сходимости ряда.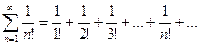
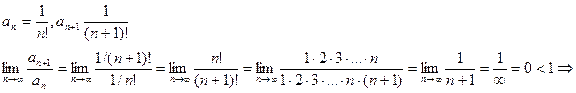 ряд сходится.
ряд сходится.