Содержание
1. Множества. Действительные числа
Понятие множества
Операции над множествами
Множество действительных чисел
Числовые последовательности
2. Функция
Понятие функции
Бесконечно малые и бесконечно большие функции
3. Непрерывность функции
Непрерывность функции в точке
Арифметические операции над функциями, непрерывными в точке
Непрерывность элементарных функций
Свойства непрерывных функций
Множества. Действительные числа
Понятие множества
Мно́жество - один из ключевых объектов математики, в частности, теории множеств и логики. Понятие множества обычно принимается за одно из исходных аксиоматических понятий, то есть не сводимое к другим понятиям, а значит и не имеющее определения. Однако, можно дать описание множества, например в формулировке немецкого математика Георга Кантора: "Под множеством мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться элементами множества)".
С 1872 г. по 1897 г. (главным образом в 1872-1884 гг.) Георг Кантор опубликовал ряд работ, в которых были систематически изложены основные разделы теории множеств. Поэтому общепризнано, что теорию множеств создал Георг Кантор. Unter einer ‚Menge‘ verstehen wir Zusammenfassung M von bestimmten wohlunterschiedenen Objecten m unsere Anschauung order unseres Denkens (welche die ‚Elementen‘ von M genannt werden) zu einem Ganzen.
Другая формулировка принадлежит английскому математику Бертрану Расселлу (1872-1970гг.): " Множество суть совокупность различных элементов, мыслимая как единое целое".
Таким образом, под множеством понимается совокупность элементов (объектов) той или иной природы.
Множества обычно обозначают большими буквами латинского или другого алфавита: 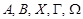 …, а элементы множества малыми буквами
…, а элементы множества малыми буквами 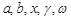 …
…
Если элемент 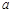 принадлежит множеству
принадлежит множеству  , то пишут
, то пишут 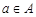 . Если
. Если 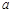 не принадлежит множеству
не принадлежит множеству  , то запись этого утверждения имеет вид
, то запись этого утверждения имеет вид 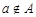 .
.
множество функция непрерывная число
Множества  и
и  называются равными, если они состоят из одних и тех же элементов, то есть равенство
называются равными, если они состоят из одних и тех же элементов, то есть равенство 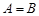 означает, что одно и тоже множество обозначено разными буквами.
означает, что одно и тоже множество обозначено разными буквами.
Существует два основных способа задания множества. Если элементы множества могут быть перечислены, то такое множество записывают в виде 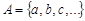 . Эта запись означает, что множество
. Эта запись означает, что множество  состоит из элементов
состоит из элементов 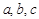 и возможно еще каких-то других. Список элементов может быть и бесконечным. Например, множество
и возможно еще каких-то других. Список элементов может быть и бесконечным. Например, множество 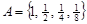 содержит четыре элемента:
содержит четыре элемента: 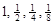 . Множество
. Множество 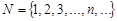 , где
, где 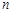 - целое положительное число, состоит из бесконечного числа элементов. Если множество состоит из элементов
- целое положительное число, состоит из бесконечного числа элементов. Если множество состоит из элементов 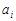 , где индекс
, где индекс 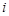 принимает значения из некоторого множества
принимает значения из некоторого множества 
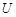 , то его записывают в виде
, то его записывают в виде 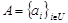 .
.
Если множество  состоит из элементов, обладающих определенным свойством, то его записывают в виде
состоит из элементов, обладающих определенным свойством, то его записывают в виде 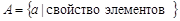 , где в фигурных скобках после вертикальной черты указывают данное свойства элементов множества. Например, если множество
, где в фигурных скобках после вертикальной черты указывают данное свойства элементов множества. Например, если множество  - это отрезок
- это отрезок 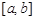 (
(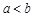 ), то есть множество всех чисел
), то есть множество всех чисел 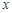 , удовлетворяющих неравенству
, удовлетворяющих неравенству 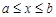 , то форма записи множества
, то форма записи множества  имеет вид
имеет вид 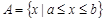 .
.
Пример. Запись 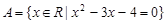 означает, что множество
означает, что множество  состоит из вещественных корней квадратного уравнения
состоит из вещественных корней квадратного уравнения 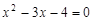 , то есть
, то есть 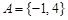 .
.
Пустым множеством называется множество, не содержащее ни одного элемента. Оно обозначается символом 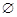 .
.
Множество  называется подмножеством множества
называется подмножеством множества  , если каждый элемент множества
, если каждый элемент множества  принадлежит множеству
принадлежит множеству  . В этом случае пишут
. В этом случае пишут 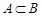 . Последнюю запись можно прочитать и так: множество
. Последнюю запись можно прочитать и так: множество  заключено (содержится) в множестве
заключено (содержится) в множестве  .
.
Если 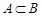 и
и 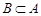 , то каждый элемент множества
, то каждый элемент множества  принадлежит множеству
принадлежит множеству  , а каждый элемент множества
, а каждый элемент множества  принадлежит множеству
принадлежит множеству  . Следовательно, множества
. Следовательно, множества  и
и  состоят из одних и тех же элементов, то есть
состоят из одних и тех же элементов, то есть 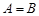 .
.
Операции над множествами
Пусть  и
и  - произвольные множества.
- произвольные множества.
Объединением или суммой множеств  и
и  называется множество
называется множество 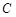 , состоящее из всех элементов, принадлежащих хотя бы одному из множеств
, состоящее из всех элементов, принадлежащих хотя бы одному из множеств  и
и  . Объединение множеств
. Объединение множеств  и
и  обозначается символом
обозначается символом 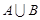 .
.
Пересечением множеств  и
и  называется множество
называется множество 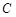 , состоящее из всех элементов, принадлежащих как множеству
, состоящее из всех элементов, принадлежащих как множеству  , так и множеству
, так и множеству  , Пересечение множеств
, Пересечение множеств  и
и  обозначается через
обозначается через 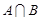 .
.
Разностью множеств  и
и  называется множество
называется множество 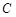 , состоящее из элементов, принадлежащих множеству
, состоящее из элементов, принадлежащих множеству  , но не принадлежащих множеству
, но не принадлежащих множеству  , то есть
, то есть 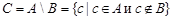 .
.
Если 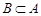 , то разность
, то разность 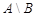 называется дополнением множества
называется дополнением множества  до множества
до множества  и обозначается
и обозначается 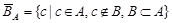 .
.
Для наглядности множества нередко изображают в виде некоторой совокупности точек на плоскости. На рис.1а изображены множества  и
и  , на рис.1б - их объединение, на рис.1в - пересечение множеств
, на рис.1б - их объединение, на рис.1в - пересечение множеств  и
и  , на рис.1г - разность множеств
, на рис.1г - разность множеств  и
и  , на рис.1д - дополнение множества
, на рис.1д - дополнение множества  до множества
до множества  .
.
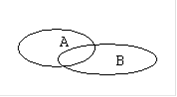
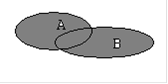
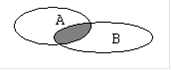
а) б) 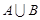 в)
в) 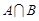
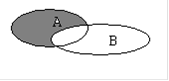
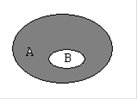
г) 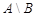 д)
д) 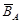
Рис.1
Пусть задана система множеств 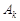 , где значения
, где значения 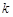 образуют некоторую совокупность индексов
образуют некоторую совокупность индексов 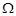 . Объединением
. Объединением 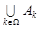 множеств
множеств 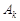 называется множество, каждый элемент которого принадлежит хотя бы одному из множеств
называется множество, каждый элемент которого принадлежит хотя бы одному из множеств 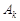 . Пересечением
. Пересечением 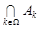 множеств
множеств 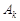 называется множество, каждый элемент которого принадлежит одновременно всем множествам
называется множество, каждый элемент которого принадлежит одновременно всем множествам 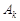 .
.
Пример. Пусть 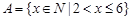 ,
, 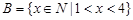 ,
, 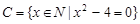 , где
, где 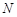 - множество натуральных чисел. Тогда
- множество натуральных чисел. Тогда
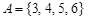 ,
, 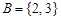 ,
, 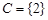 ,
,
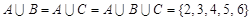 ,
, 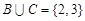 ,
,
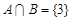 ,
, 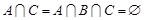 ,
, 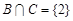 ,
,
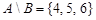 ,
, 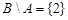 ,
, 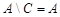 ,
, 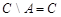 ,
, 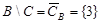 .
.
Логические символы
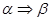 - означает "из предложения
- означает "из предложения 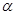 следует предложение
следует предложение 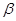 ";
";
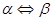 - означает " предложения
- означает " предложения 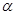 и
и 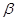 равносильны, т.е. из
равносильны, т.е. из 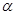 следует
следует 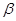 и
и
из 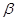 следует
следует 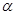 ;
;
: - означает "имеет место", "такое что";
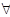 - (символ всеобщности) означает "для любого", "для всякого";
- (символ всеобщности) означает "для любого", "для всякого";
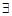 - (символом существования) означает "найдется", "существует".
- (символом существования) означает "найдется", "существует".
Например, запись 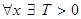 означает "для любого
означает "для любого 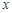 найдется положительное число
найдется положительное число 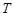 ".
".
Числовые последовательности
Определение. Если каждому натуральному числу 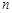 ставится в соответствие по определенному закону некоторое вещественное число
ставится в соответствие по определенному закону некоторое вещественное число 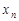 , то совокупность занумерованных чисел
, то совокупность занумерованных чисел 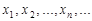 называют числовой последовательностью или просто последовательностью.
называют числовой последовательностью или просто последовательностью.
Числа 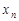 называются элементами или членами последовательности. По своему определению последовательность содержит бесконечное множество элементов. Последовательность с элементами
называются элементами или членами последовательности. По своему определению последовательность содержит бесконечное множество элементов. Последовательность с элементами 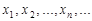 обозначают также {
обозначают также { 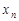 }.
}.
Например, 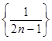 - это последовательность
- это последовательность 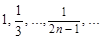 ,
,
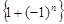 - это последовательность 0, 2, 0, 2, …
- это последовательность 0, 2, 0, 2, …
Последовательность может быть задана с помощью формулы 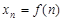 , которая называется формулой общего члена последовательности. Например, формула
, которая называется формулой общего члена последовательности. Например, формула  задает последовательность
задает последовательность 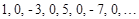
Суммой (разностью) двух последовательностей 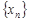 и
и 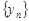 называется последовательность
называется последовательность 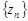 , все элементы которой равны сумме (разности)
, все элементы которой равны сумме (разности) 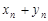 (
(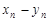 ).
).
Произведением двух последовательностей 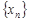 и
и 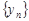 называется последовательность
называется последовательность 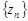 =
= 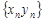 , частным - последовательность
, частным - последовательность 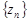 =
= 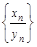 , причем при определении частного нужно потребовать, чтобы все элементы последовательности
, причем при определении частного нужно потребовать, чтобы все элементы последовательности 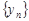 были отличны от нуля.
были отличны от нуля.
Ограниченные и неограниченные последовательности
Определение. Последовательность 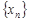 называется ограниченной сверху (снизу), если найдется такое вещественное число
называется ограниченной сверху (снизу), если найдется такое вещественное число 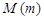 , что для всех членов последовательности справедливо неравенство
, что для всех членов последовательности справедливо неравенство 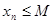 (
(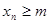 ).
).
Последовательность 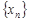 называется ограниченной, если она ограничена и сверху и снизу, т.е. если найдутся такие вещественные числа
называется ограниченной, если она ограничена и сверху и снизу, т.е. если найдутся такие вещественные числа 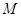 и
и 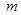 , что для всех членов последовательности справедливо неравенство
, что для всех членов последовательности справедливо неравенство 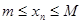 .
.
Это определение можно сформулировать по другому:
Последовательность 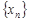 называется ограниченной, если найдется положительное число
называется ограниченной, если найдется положительное число 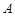 такое, что для всех членов последовательности справедливо неравенство
такое, что для всех членов последовательности справедливо неравенство 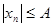 . (Здесь
. (Здесь 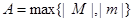 ).
).
Последовательность 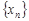 называется неограниченной, если для любого положительного числа
называется неограниченной, если для любого положительного числа 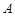 найдется хотя бы один элемент последовательности, удовлетворяющий неравенству
найдется хотя бы один элемент последовательности, удовлетворяющий неравенству 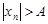 .
.
Примеры.1. 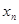 =
= 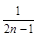 - ограниченная последовательность, так как
- ограниченная последовательность, так как 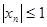 .
.
. 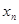 =
= 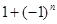 - ограниченная последовательность, так как
- ограниченная последовательность, так как 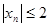 .
.
. 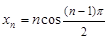 - неограниченная последовательность {
- неограниченная последовательность { 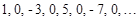 }, так как для любого положительного числа
}, так как для любого положительного числа 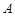 найдется хотя бы один элемент последовательности, удовлетворяющий неравенству
найдется хотя бы один элемент последовательности, удовлетворяющий неравенству 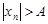 .
.
Бесконечно большие и бесконечно малые последовательности
Определение. Последовательность 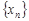 называется бесконечно большой, если для любого положительного числа
называется бесконечно большой, если для любого положительного числа 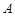 найдется номер
найдется номер 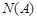 , зависящий от
, зависящий от 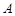 , такой, что для всех номеров
, такой, что для всех номеров 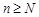 справедливо неравенство
справедливо неравенство 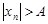 .
.
Пример. Последовательность 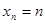 , то есть последовательность натуральных чисел {
, то есть последовательность натуральных чисел { 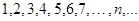 } является бесконечно большой, так как для любого положительного числа
} является бесконечно большой, так как для любого положительного числа 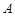 найдется номер
найдется номер 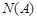 , такой, что для всех номеров
, такой, что для всех номеров 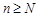 справедливо неравенство
справедливо неравенство 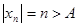 .
.
Очевидно, что любая бесконечно большая последовательность является неограниченной. Действительно, для того, чтобы последовательность была неограниченной необходимо, чтобы для любого положительного числа 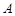 неравенство
неравенство 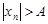 выполнялось, хотя бы для одного элемента последовательности, но из определения бесконечно большой последовательности следует, что такими элементами являются все элементы последовательности, начиная с некоторого номера
выполнялось, хотя бы для одного элемента последовательности, но из определения бесконечно большой последовательности следует, что такими элементами являются все элементы последовательности, начиная с некоторого номера 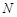 .
.
Обратное утверждение неверно, то есть неограниченная последовательность не всегда является бесконечно большой.
Пример. Рассмотрим последовательность 0, 2, 0, 4, …, у которой все члены с нечетными номерами равны нулю, а члены с четными номерами 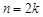
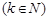 равны
равны 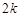 . Поскольку для любого положительного числа
. Поскольку для любого положительного числа 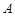 найдется натуральное число
найдется натуральное число 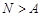 , то для четных номеров
, то для четных номеров 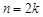 больших
больших 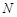 справедливо неравенство
справедливо неравенство 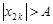 . Следовательно, данная последовательность является неограниченной. Однако она не является бесконечно большой, так как, какой бы большой номер
. Следовательно, данная последовательность является неограниченной. Однако она не является бесконечно большой, так как, какой бы большой номер 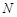 мы не взяли, имеются члены с нечетными номерами
мы не взяли, имеются члены с нечетными номерами 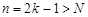 , равные нулю, для которых неравенство
, равные нулю, для которых неравенство 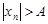 не имеет места.
не имеет места.
Определение. Последовательность 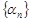 называется бесконечно малой, если для любого положительного числа
называется бесконечно малой, если для любого положительного числа 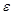 найдется номер
найдется номер 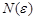 , зависящий от
, зависящий от 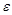 , такой, что при
, такой, что при 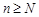 все элементы
все элементы 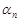 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству 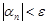 .
.
Пример. Показать, что последовательность 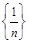 является бесконечно малой.
является бесконечно малой.
Пусть 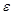 - произвольное положительное число. Тогда
- произвольное положительное число. Тогда 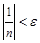 при всех
при всех 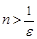 , то есть за номер
, то есть за номер 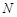 можно принять натуральное число
можно принять натуральное число 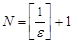 , где
, где 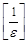 - целая часть числа
- целая часть числа 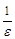 . Поскольку для произвольного числа
. Поскольку для произвольного числа  мы смогли определить номер
мы смогли определить номер 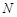 такой, что при всех
такой, что при всех 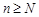 справедливо неравенство
справедливо неравенство 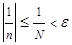 , то последовательность
, то последовательность 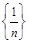 - бесконечно малая.
- бесконечно малая.
Пример. Показать, что последовательность 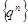 является бесконечно большой, если
является бесконечно большой, если 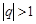 , и бесконечно малой, если
, и бесконечно малой, если 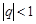 .
.
) Пусть 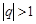 . Возьмем произвольное положительное число
. Возьмем произвольное положительное число 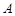 . Тогда
. Тогда 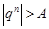 , при всех
, при всех 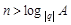 . Возьмем
. Возьмем 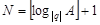 . Тогда для всех
. Тогда для всех 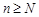 справедлива цепочка неравенств
справедлива цепочка неравенств 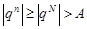 . Следовательно, последовательность
. Следовательно, последовательность 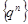 является бесконечно большой.
является бесконечно большой.
) Если 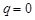 , то для любого положительного числа
, то для любого положительного числа 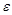 и любого номера
и любого номера 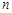 выполняется неравенство
выполняется неравенство 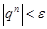 , и последовательность
, и последовательность 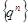 - бесконечно малая. Рассмотрим случай
- бесконечно малая. Рассмотрим случай 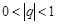 . В этом случае
. В этом случае 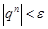 , при всех
, при всех 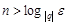 . Возьмем
. Возьмем 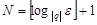 . Тогда при всех
. Тогда при всех 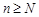
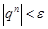 . Следовательно, если
. Следовательно, если 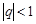 , то последовательность
, то последовательность 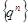 является бесконечно малой.
является бесконечно малой.
Предел числовой последовательности. Сходящиеся последовательности
Определение 1. Число 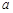 называется пределом последовательности
называется пределом последовательности 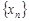 , если для любого положительного числа
, если для любого положительного числа 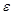 найдется такой номер
найдется такой номер 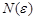 , зависящий от
, зависящий от 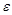 , что при
, что при 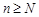 все элементы
все элементы 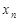 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству
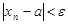 . (1)
. (1)
Символически это записывают так
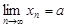 , или
, или 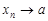 при
при 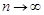 .
.
Неравенство (1) означает, что, начиная с номера 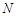 , все элементы последовательности находятся внутри интервала
, все элементы последовательности находятся внутри интервала 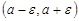 , который называют
, который называют 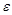 -окрестностью числа
-окрестностью числа 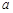 .
.
Согласно данному определению бесконечно малая последовательность 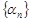 имеет своим пределом нуль, то есть
имеет своим пределом нуль, то есть 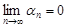 .
.
Если последовательность 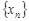 является бесконечно большой, то пишут
является бесконечно большой, то пишут 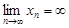 . В случае бесконечно большой последовательности, все члены которой, начиная с некоторого номера положительны, говорят, что ее предел равен
. В случае бесконечно большой последовательности, все члены которой, начиная с некоторого номера положительны, говорят, что ее предел равен 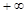 и пишут
и пишут 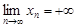 . Если же все члены бесконечно большой последовательности, начиная с некоторого номера отрицательны, то ее предел считают равным
. Если же все члены бесконечно большой последовательности, начиная с некоторого номера отрицательны, то ее предел считают равным 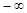 и пишут
и пишут 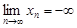 .
.
Определение 2. Число  называется пределом последовательности
называется пределом последовательности 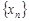 , если в любой
, если в любой 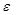 -окрестности числа
-окрестности числа  находятся все элементы данной последовательности, начиная с некоторого номера.
находятся все элементы данной последовательности, начиная с некоторого номера.
Последнее утверждение означает, что, если число  - предел последовательности, то за пределами любой его
- предел последовательности, то за пределами любой его 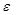 -окрестности находится лишь конечное число элементов данной последовательности.
-окрестности находится лишь конечное число элементов данной последовательности.
Определение. Последовательность 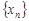 называется сходящейся, если она имеет конечный предел. Если предел не существует или равен
называется сходящейся, если она имеет конечный предел. Если предел не существует или равен 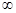 , то последовательность называется расходящейся.
, то последовательность называется расходящейся.
Из определения 2 следует, что последовательность расходится, если для любого числа  найдется его
найдется его 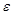 -окрестность, за пределами которой лежит бесконечное число элементов последовательности.
-окрестность, за пределами которой лежит бесконечное число элементов последовательности.
Пример 1. Рассмотрим последовательность 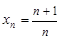 . Покажем, что
. Покажем, что 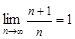 .
.
Пусть 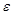 - произвольное положительное число. Тогда неравенство
- произвольное положительное число. Тогда неравенство 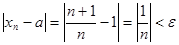 выполняется при всех
выполняется при всех 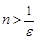 , то есть за номер
, то есть за номер 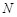 можно принять натуральное число
можно принять натуральное число 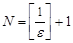 , где
, где 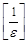 - целая часть числа
- целая часть числа 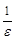 . Поскольку для произвольного числа
. Поскольку для произвольного числа 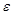 мы смогли определить номер
мы смогли определить номер 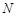 такой, что при всех
такой, что при всех 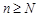 справедливо неравенство
справедливо неравенство 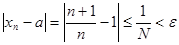 , то последовательность
, то последовательность  сходится, а ее предел равен единице, то есть
сходится, а ее предел равен единице, то есть 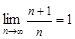 .
.
Пример 2. Последовательность 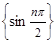 расходится.
расходится.
Действительно, данная последовательность - это последовательность 1, 0, - 1, 0, 1, 0, - 1, … Пусть 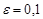 . Если, число
. Если, число  принадлежит интервалу
принадлежит интервалу 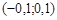 , то в
, то в 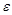 -окрестность этого числа попадут лишь члены последовательности, равные нулю, а бесконечное число членов, равных 1 или - 1, окажутся за пределами
-окрестность этого числа попадут лишь члены последовательности, равные нулю, а бесконечное число членов, равных 1 или - 1, окажутся за пределами 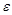 -окрестности. Если число
-окрестности. Если число  принадлежит интервалу (0,9; 1,1) или (-1,1; - 0,9), то за пределами
принадлежит интервалу (0,9; 1,1) или (-1,1; - 0,9), то за пределами 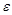 -окрестности заведомо окажутся все нулевые члены последовательности. При всех остальных значениях числа
-окрестности заведомо окажутся все нулевые члены последовательности. При всех остальных значениях числа  в его
в его 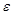 -окрестность не попадет ни одного члена последовательности. Итак какое бы число
-окрестность не попадет ни одного члена последовательности. Итак какое бы число  мы не взяли, для заданного
мы не взяли, для заданного 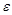 найдется бесконечное число элементов последовательности, не принадлежащих
найдется бесконечное число элементов последовательности, не принадлежащих 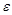 -окрестности числа
-окрестности числа  . Следовательно, рассматриваемая последовательность расходится.
. Следовательно, рассматриваемая последовательность расходится.
Основные свойства сходящихся последовательностей.
Теорема 1. Сходящаяся последовательность имеет только один предел.
Доказательство. ( Методом от противного). Предположим, что последовательность 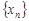 сходится и имеет два разных предела, то есть
сходится и имеет два разных предела, то есть 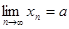 и
и 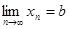 , причем
, причем 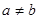 . Возьмем
. Возьмем 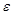 -окрестность числа а, которая не содержит b. Так как а - предел последовательности
-окрестность числа а, которая не содержит b. Так как а - предел последовательности 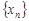 , то по определению 2 за пределами
, то по определению 2 за пределами 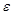 -окрестности находится лишь конечное число элементов данной последовательности и, следовательно, число b не может быть ее пределом.
-окрестности находится лишь конечное число элементов данной последовательности и, следовательно, число b не может быть ее пределом.
Теорема 2. Если все элементы последовательности равны одному и тому же числу 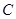 , то и предел такой последовательности также равен числу
, то и предел такой последовательности также равен числу 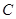 , то есть, если
, то есть, если 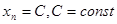 , то и
, то и 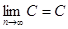 .
.
Доказательство. Рассмотрим последовательность 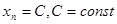 . Покажем, что
. Покажем, что 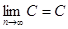 , то есть предел последовательности равен константе
, то есть предел последовательности равен константе 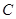 . Рассмотрим любую
. Рассмотрим любую 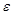 -окрестность числа С. Все члены последовательности попадут в эту окрестность, а за ее пределами не окажется ни одного члена последовательности. Согласно определению 2 это и означает, что число С есть предел данной последовательности.
-окрестность числа С. Все члены последовательности попадут в эту окрестность, а за ее пределами не окажется ни одного члена последовательности. Согласно определению 2 это и означает, что число С есть предел данной последовательности.
Теорема 3. Сумма, разность, произведение и частное двух сходящихся последовательностей 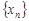 и
и 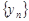 (частное при условии, что предел
(частное при условии, что предел 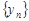 отличен от нуля) есть сходящаяся последовательность, предел которой равен соответственно сумме, разности, произведению и частному пределов последовательностей
отличен от нуля) есть сходящаяся последовательность, предел которой равен соответственно сумме, разности, произведению и частному пределов последовательностей 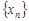 и
и 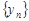 , то есть, если
, то есть, если
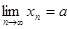 ,
, 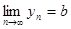 , то
, то
) 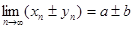 ;
;
) 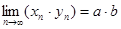 ;
;
) 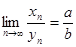 ,
, 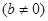 .
.
Доказательство. Докажем свойство 1) для суммы двух сходящихся последовательностей, то есть докажем, что 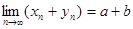 . Возьмем любое положительное число
. Возьмем любое положительное число 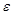 . Поскольку
. Поскольку 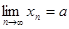 , то для положительного числа
, то для положительного числа 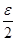 существует номер
существует номер 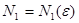 такой, что при всех
такой, что при всех 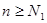 выполняется неравенство
выполняется неравенство 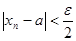 . Аналогично, так как
. Аналогично, так как 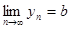 то для положительного числа
то для положительного числа 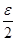 существует номер
существует номер 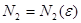 такой, что при всех
такой, что при всех 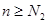 выполняется неравенство
выполняется неравенство 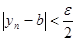 . Обозначим
. Обозначим 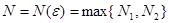 . Тогда при всех
. Тогда при всех 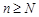 справедливо
справедливо
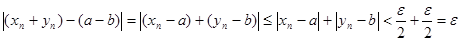 .
.
Это и означает, что 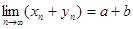 , что и требовалось доказать.
, что и требовалось доказать.
Следствие. Постоянный множитель можно выносить за знак предела, то есть
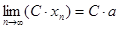 , где
, где 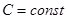 .
.
Теорема 4. Сходящаяся последовательность ограничена.
Теорема 5. Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью.
То есть, если 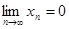 , а последовательность {
, а последовательность { 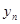 } - ограниченная, то
} - ограниченная, то 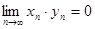 .
.
Доказательство. Пусть { 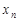 } - бесконечно малая, а {
} - бесконечно малая, а { 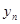 } - ограниченная последовательности. Требуется доказать, что последовательность
} - ограниченная последовательности. Требуется доказать, что последовательность 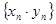 - бесконечно малая последовательность. Так как {
- бесконечно малая последовательность. Так как { 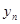 } - ограниченная, то существует положительное число
} - ограниченная, то существует положительное число 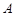 такое, что для всех членов последовательности справедливо неравенство
такое, что для всех членов последовательности справедливо неравенство 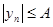 . Возьмем любое положительное число
. Возьмем любое положительное число 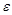 . Поскольку {
. Поскольку { 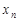 } - бесконечно малая, то для положительного числа
} - бесконечно малая, то для положительного числа 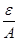 существует номер
существует номер 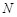 такой, что при всех
такой, что при всех 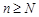 выполняется неравенство
выполняется неравенство 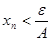 . Тогда при всех
. Тогда при всех 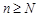 справедливо
справедливо
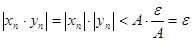 .
.
Это означает, что последовательность 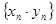 - бесконечно малая.
- бесконечно малая.
Пример. Последовательность 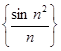 - бесконечно малая как произведение ограниченной последовательности
- бесконечно малая как произведение ограниченной последовательности 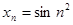 и бесконечно малой
и бесконечно малой 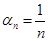 . Следовательно,
. Следовательно, 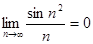 .
.
Теорема 6. Если последовательность { 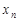 } - бесконечно большая, то, начиная с некоторого номера, определена последовательность
} - бесконечно большая, то, начиная с некоторого номера, определена последовательность 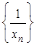 , которая является бесконечно малой. Если все элементы бесконечно малой последовательности
, которая является бесконечно малой. Если все элементы бесконечно малой последовательности 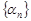 не равны нулю, то последовательность
не равны нулю, то последовательность 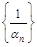 - бесконечно большая.
- бесконечно большая.
(Без доказательства).
Теорема 7 (о трех последовательностях). Пусть последов



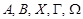 …, а элементы множества малыми буквами
…, а элементы множества малыми буквами 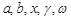 …
…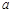 принадлежит множеству
принадлежит множеству  , то пишут
, то пишут 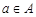 . Если
. Если 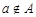 .
. называются равными, если они состоят из одних и тех же элементов, то есть равенство
называются равными, если они состоят из одних и тех же элементов, то есть равенство 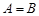 означает, что одно и тоже множество обозначено разными буквами.
означает, что одно и тоже множество обозначено разными буквами.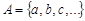 . Эта запись означает, что множество
. Эта запись означает, что множество 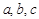 и возможно еще каких-то других. Список элементов может быть и бесконечным. Например, множество
и возможно еще каких-то других. Список элементов может быть и бесконечным. Например, множество 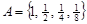 содержит четыре элемента:
содержит четыре элемента: 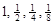 . Множество
. Множество 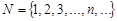 , где
, где 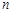 - целое положительное число, состоит из бесконечного числа элементов. Если множество состоит из элементов
- целое положительное число, состоит из бесконечного числа элементов. Если множество состоит из элементов 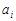 , где индекс
, где индекс 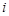 принимает значения из некоторого множества
принимает значения из некоторого множества 
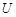 , то его записывают в виде
, то его записывают в виде 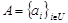 .
.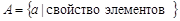 , где в фигурных скобках после вертикальной черты указывают данное свойства элементов множества. Например, если множество
, где в фигурных скобках после вертикальной черты указывают данное свойства элементов множества. Например, если множество 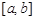 (
(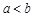 ), то есть множество всех чисел
), то есть множество всех чисел 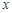 , удовлетворяющих неравенству
, удовлетворяющих неравенству 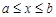 , то форма записи множества
, то форма записи множества 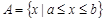 .
.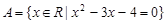 означает, что множество
означает, что множество 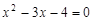 , то есть
, то есть 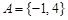 .
.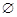 .
.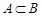 . Последнюю запись можно прочитать и так: множество
. Последнюю запись можно прочитать и так: множество 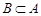 , то каждый элемент множества
, то каждый элемент множества 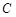 , состоящее из всех элементов, принадлежащих хотя бы одному из множеств
, состоящее из всех элементов, принадлежащих хотя бы одному из множеств 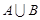 .
.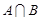 .
.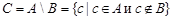 .
.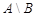 называется дополнением множества
называется дополнением множества 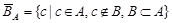 .
.


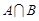


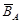
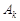 , где значения
, где значения 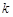 образуют некоторую совокупность индексов
образуют некоторую совокупность индексов 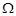 . Объединением
. Объединением 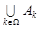 множеств
множеств 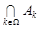 множеств
множеств 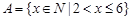 ,
, 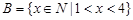 ,
, 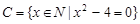 , где
, где 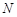 - множество натуральных чисел. Тогда
- множество натуральных чисел. Тогда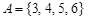 ,
, 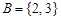 ,
, 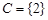 ,
,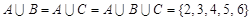 ,
, 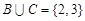 ,
,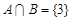 ,
, 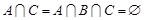 ,
, 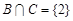 ,
,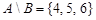 ,
, 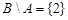 ,
, 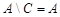 ,
, 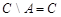 ,
, 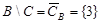 .
.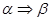 - означает "из предложения
- означает "из предложения 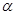 следует предложение
следует предложение 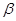 ";
";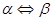 - означает " предложения
- означает " предложения 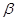 равносильны, т.е. из
равносильны, т.е. из 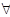 - (символ всеобщности) означает "для любого", "для всякого";
- (символ всеобщности) означает "для любого", "для всякого";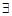 - (символом существования) означает "найдется", "существует".
- (символом существования) означает "найдется", "существует".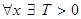 означает "для любого
означает "для любого 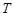 ".
".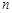 ставится в соответствие по определенному закону некоторое вещественное число
ставится в соответствие по определенному закону некоторое вещественное число 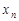 , то совокупность занумерованных чисел
, то совокупность занумерованных чисел 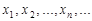 называют числовой последовательностью или просто последовательностью.
называют числовой последовательностью или просто последовательностью.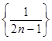 - это последовательность
- это последовательность 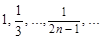 ,
,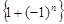 - это последовательность 0, 2, 0, 2, …
- это последовательность 0, 2, 0, 2, …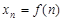 , которая называется формулой общего члена последовательности. Например, формула
, которая называется формулой общего члена последовательности. Например, формула  задает последовательность
задает последовательность 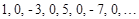
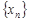 и
и 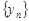 называется последовательность
называется последовательность 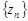 , все элементы которой равны сумме (разности)
, все элементы которой равны сумме (разности) 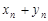 (
(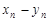 ).
).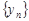 называется последовательность
называется последовательность 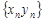 , частным - последовательность
, частным - последовательность 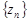 =
= 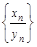 , причем при определении частного нужно потребовать, чтобы все элементы последовательности
, причем при определении частного нужно потребовать, чтобы все элементы последовательности 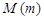 , что для всех членов последовательности справедливо неравенство
, что для всех членов последовательности справедливо неравенство 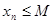 (
(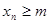 ).
).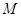 и
и 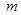 , что для всех членов последовательности справедливо неравенство
, что для всех членов последовательности справедливо неравенство 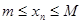 .
.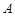 такое, что для всех членов последовательности справедливо неравенство
такое, что для всех членов последовательности справедливо неравенство 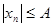 . (Здесь
. (Здесь 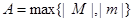 ).
).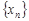 называется неограниченной, если для любого положительного числа
называется неограниченной, если для любого положительного числа 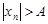 .
.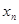 =
= 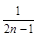 - ограниченная последовательность, так как
- ограниченная последовательность, так как 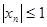 .
.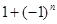 - ограниченная последовательность, так как
- ограниченная последовательность, так как 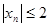 .
.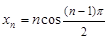 - неограниченная последовательность {
- неограниченная последовательность { 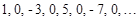 }, так как для любого положительного числа
}, так как для любого положительного числа 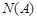 , зависящий от
, зависящий от 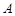 , такой, что для всех номеров
, такой, что для всех номеров 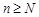 справедливо неравенство
справедливо неравенство 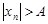 .
.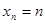 , то есть последовательность натуральных чисел {
, то есть последовательность натуральных чисел { 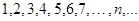 } является бесконечно большой, так как для любого положительного числа
} является бесконечно большой, так как для любого положительного числа 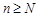 справедливо неравенство
справедливо неравенство 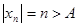 .
.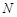 .
.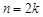
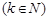 равны
равны 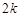 . Поскольку для любого положительного числа
. Поскольку для любого положительного числа 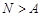 , то для четных номеров
, то для четных номеров 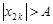 . Следовательно, данная последовательность является неограниченной. Однако она не является бесконечно большой, так как, какой бы большой номер
. Следовательно, данная последовательность является неограниченной. Однако она не является бесконечно большой, так как, какой бы большой номер 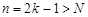 , равные нулю, для которых неравенство
, равные нулю, для которых неравенство 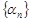 называется бесконечно малой, если для любого положительного числа
называется бесконечно малой, если для любого положительного числа 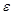 найдется номер
найдется номер 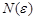 , зависящий от
, зависящий от 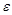 , такой, что при
, такой, что при 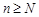 все элементы
все элементы 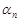 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству 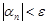 .
.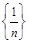 является бесконечно малой.
является бесконечно малой.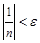 при всех
при всех 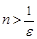 , то есть за номер
, то есть за номер 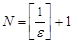 , где
, где 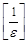 - целая часть числа
- целая часть числа 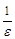 . Поскольку для произвольного числа
. Поскольку для произвольного числа 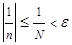 , то последовательность
, то последовательность 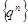 является бесконечно большой, если
является бесконечно большой, если 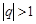 , и бесконечно малой, если
, и бесконечно малой, если 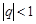 .
.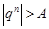 , при всех
, при всех 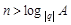 . Возьмем
. Возьмем 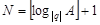 . Тогда для всех
. Тогда для всех 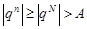 . Следовательно, последовательность
. Следовательно, последовательность 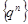 является бесконечно большой.
является бесконечно большой.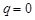 , то для любого положительного числа
, то для любого положительного числа 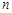 выполняется неравенство
выполняется неравенство 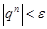 , и последовательность
, и последовательность 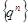 - бесконечно малая. Рассмотрим случай
- бесконечно малая. Рассмотрим случай 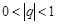 . В этом случае
. В этом случае 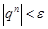 , при всех
, при всех 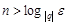 . Возьмем
. Возьмем 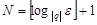 . Тогда при всех
. Тогда при всех 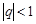 , то последовательность
, то последовательность 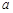 называется пределом последовательности
называется пределом последовательности 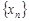 , если для любого положительного числа
, если для любого положительного числа 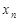 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству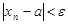 . (1)
. (1)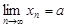 , или
, или 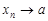 при
при 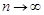 .
.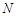 , все элементы последовательности находятся внутри интервала
, все элементы последовательности находятся внутри интервала 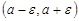 , который называют
, который называют 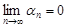 .
.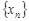 является бесконечно большой, то пишут
является бесконечно большой, то пишут 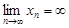 . В случае бесконечно большой последовательности, все члены которой, начиная с некоторого номера положительны, говорят, что ее предел равен
. В случае бесконечно большой последовательности, все члены которой, начиная с некоторого номера положительны, говорят, что ее предел равен 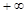 и пишут
и пишут 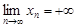 . Если же все члены бесконечно большой последовательности, начиная с некоторого номера отрицательны, то ее предел считают равным
. Если же все члены бесконечно большой последовательности, начиная с некоторого номера отрицательны, то ее предел считают равным 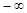 и пишут
и пишут 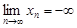 .
. называется пределом последовательности
называется пределом последовательности 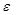 -окрестности числа
-окрестности числа 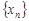 называется сходящейся, если она имеет конечный предел. Если предел не существует или равен
называется сходящейся, если она имеет конечный предел. Если предел не существует или равен 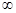 , то последовательность называется расходящейся.
, то последовательность называется расходящейся.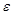 -окрестность, за пределами которой лежит бесконечное число элементов последовательности.
-окрестность, за пределами которой лежит бесконечное число элементов последовательности.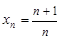 . Покажем, что
. Покажем, что 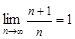 .
.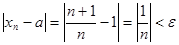 выполняется при всех
выполняется при всех 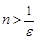 , то есть за номер
, то есть за номер 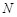 можно принять натуральное число
можно принять натуральное число 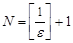 , где
, где 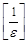 - целая часть числа
- целая часть числа 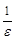 . Поскольку для произвольного числа
. Поскольку для произвольного числа  такой, что при всех
такой, что при всех 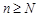 справедливо неравенство
справедливо неравенство 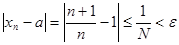 , то последовательность
, то последовательность 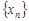 сходится, а ее предел равен единице, то есть
сходится, а ее предел равен единице, то есть 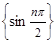 расходится.
расходится.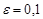 . Если, число
. Если, число 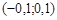 , то в
, то в 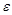 -окрестность этого числа попадут лишь члены последовательности, равные нулю, а бесконечное число членов, равных 1 или - 1, окажутся за пределами
-окрестность этого числа попадут лишь члены последовательности, равные нулю, а бесконечное число членов, равных 1 или - 1, окажутся за пределами 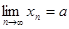 и
и 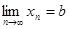 , причем
, причем 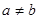 . Возьмем
. Возьмем 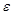 -окрестности находится лишь конечное число элементов данной последовательности и, следовательно, число b не может быть ее пределом.
-окрестности находится лишь конечное число элементов данной последовательности и, следовательно, число b не может быть ее пределом.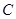 , то и предел такой последовательности также равен числу
, то и предел такой последовательности также равен числу 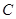 , то есть, если
, то есть, если 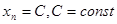 , то и
, то и 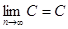 .
.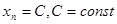 . Покажем, что
. Покажем, что 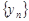 (частное при условии, что предел
(частное при условии, что предел 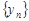 отличен от нуля) есть сходящаяся последовательность, предел которой равен соответственно сумме, разности, произведению и частному пределов последовательностей
отличен от нуля) есть сходящаяся последовательность, предел которой равен соответственно сумме, разности, произведению и частному пределов последовательностей 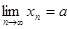 ,
, 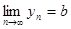 , то
, то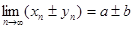 ;
;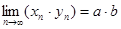 ;
;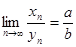 ,
,  .
.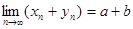 . Возьмем любое положительное число
. Возьмем любое положительное число 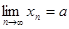 , то для положительного числа
, то для положительного числа 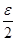 существует номер
существует номер  такой, что при всех
такой, что при всех 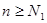 выполняется неравенство
выполняется неравенство 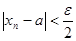 . Аналогично, так как
. Аналогично, так как 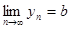 то для положительного числа
то для положительного числа 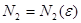 такой, что при всех
такой, что при всех 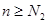 выполняется неравенство
выполняется неравенство 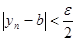 . Обозначим
. Обозначим 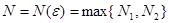 . Тогда при всех
. Тогда при всех 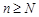 справедливо
справедливо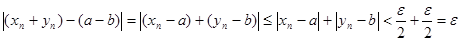 .
.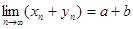 , что и требовалось доказать.
, что и требовалось доказать.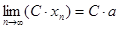 , где
, где  .
.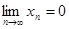 , а последовательность {
, а последовательность { 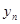 } - ограниченная, то
} - ограниченная, то 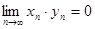 .
.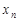 } - бесконечно малая, а {
} - бесконечно малая, а { 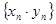 - бесконечно малая последовательность. Так как {
- бесконечно малая последовательность. Так как { 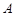 такое, что для всех членов последовательности справедливо неравенство
такое, что для всех членов последовательности справедливо неравенство 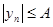 . Возьмем любое положительное число
. Возьмем любое положительное число 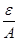 существует номер
существует номер 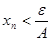 . Тогда при всех
. Тогда при всех 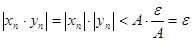 .
.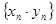 - бесконечно малая.
- бесконечно малая.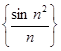 - бесконечно малая как произведение ограниченной последовательности
- бесконечно малая как произведение ограниченной последовательности 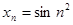 и бесконечно малой
и бесконечно малой 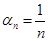 . Следовательно,
. Следовательно, 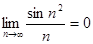 .
. , которая является бесконечно малой. Если все элементы бесконечно малой последовательности
, которая является бесконечно малой. Если все элементы бесконечно малой последовательности 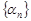 не равны нулю, то последовательность
не равны нулю, то последовательность 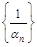 - бесконечно большая.
- бесконечно большая.


