МОДУЛЬ I
ВВЕДЕНИЕ
Механика – дисциплина, при изучении которой студенты в первую очередь могут проследить функционирование математической модели и сопоставить ее с реальным процессом. Апробация теории позволяет закрепить знания, полученные при изучении математического анализа, алгебры, аналитической геометрии и вычислительной математики. Причем все эти дисциплины используются во взаимосвязи. В их кругу теоретическая механика занимает особое место.
Это наука о законах механического движения и взаимодействия материальных тел. Имея технические корни, она развивается в теснейшей связи с курсом механики деформируемого твердого тела (и особенно с одним из ее разделов – сопротивлением материалов).
Для изучения курса важно иметь соответствующую математическую подготовку. Во всех разделах широко применяется векторная алгебра. Необходимо уметь вычислять проекции векторов на координатные оси, геометрически и аналитически находить сумму векторов, скалярное и векторное произведения, а также знать их свойства и правила дифференцирования.
Кроме того, важно уяснить сущность каждого излагаемого вопроса. Особое внимание следует уделить приобретению навыков решения задач.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
При изучении учебного курса «Теоретическая механика» студент знакомится с математическими моделями реальных явлений и существующими методами расчета, которые базируются на знаниях, полученных при изучении аналитической геометрии и линейной алгебры, векторной алгебры, высшей алгебры, основ математического анализа (табл. 1).
Табл. 1.
| Наименование дисциплины
| Раздел
| Тема
|
| Математика
| Аналитическая геометрия и линейная алгебра
| Алгебраические преобразования, решение алгебраических уравнений первого и второго порядка, Евклидова геометрия, тригонометрия, функции и графики аналитических и трансцендентных функций.
|
| Векторная алгебра
| Системы координат, преобразование систем координат, понятие вектора и линейные операции над ним, проекции векторов на оси, геометрическое и аналитическое сложение векторов, скалярное и векторное произведения векторов, решение векторных уравнений, кривые второго порядка, параметрическое задание функций.
|
| Высшая алгебра
| Системы линейных уравнений, определители, квадратичные формы, Евклидовы пространства, вычисление корней многочленов.
|
| Основы математического анализа
| Дифференцирование функций, экстремумы функций, геометрические приложения производных, неопределенный и определенный интегралы, дифференциальные уравнения, ряды.
|
Основным документом, определяющим необходимый объём знаний студентов, является программа курса, составленная на основе государственного образовательного стандарта высшего профессионального образования.
Процесс овладения студентами определенных знаний и навыков, складывается из самостоятельного изучения соответствующих разделов курса по учебникам, самостоятельного выполнения контрольных работ. Контрольная работа оформляется на бумаге формата А4, согласно правилам черчения. Оформление титульного листа контрольной работы показано на рис.1
При оформлении контрольной работы необходимо выписать для заданного варианта полное условие с числовыми данными, написать текст задания, составить аккуратный чертеж с соблюдением масштаба и показать на нем все размеры в числах. Каждый студент обязан защитить контрольные работы.
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО КГПУ им. В.П. Астафьева
Кафедра «Технология и предпринимательство»
Контрольная работа №
по кинематике
(модуль 1)
тема задания_________________
____________________________
выполнил студент (ка)_________гр.
Ф. И. О. _______________________
Проверил______________________
«___» __________________ 200 г.
Красноярск
201 г.
|
Рис. 1.
Каждый этап решения задачи в контрольной работе должен быть озаглавлен. При выполнении расчетов сначала записывается формула, затем в нее подставляются исходные данные с размерностями системы Си и подсчитывается результат. Например:

Решение должно сопровождаться краткими, последовательными и грамотными, без сокращения слов, объяснениями и чертежами, на которых должны быть показаны все размеры в числах. Необходимо указывать единицы измерения (размерность) всех полученных результатов. Задание, выполненное небрежно, без соблюдения всех перечисленных требований, не принимается.
Защита контрольных работ производится во время сессии, в сроки, установленные графиком учебного процесса в следующем порядке:
· преподаватель проверяет готовые задания, указывает на ошибки, если они имеются и задает несколько вопросов по теме выполненного задания;
· для защиты задания студенту дается задача по этой теме в виде контрольной работы;
· задание не засчитывается, если студент не смог решить предложенную преподавателем задачу. Только после дополнительного изучения темы он может повторно защитить задание.
·
Элементы тригонометрии
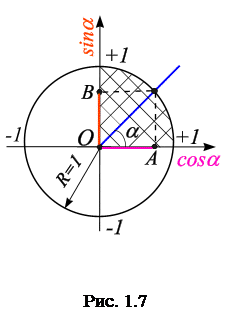
Рассмотрим круг единичного радиуса 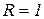 (рис. 1.7). Длина окружности круга единичного радиуса равна
(рис. 1.7). Длина окружности круга единичного радиуса равна 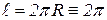 , откуда
, откуда
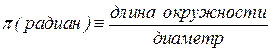
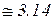
Градусная и радианная мера:
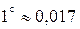 рад.
рад. 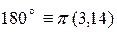 рад.;
рад.;
1 рад. 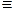
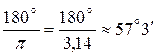 .
.
Таблица значений тригонометрических функций в смысле главного значения, т.е. в первом квадранте (рис. 1.7).
| радиан
| 0
| 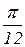
| 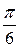
| 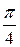
| 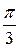
| 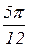
| 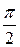
| | градус
| 0°
| 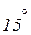
| 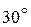
| 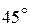
| 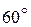
| 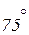
| 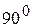
| 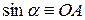
| 0
| 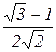
| 0,5
| 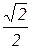
| 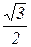
| 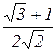
|
1
| 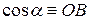
| 1
| 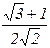
| 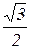
| 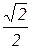
| 0,5
| 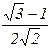
|
0
|
|
Основное тригонометрическое тождество:
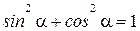 .
Функции двойного угла: .
Функции двойного угла:
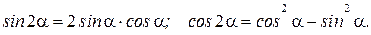 Формулы приведения:
Формулы приведения:
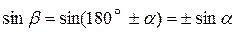 ; ; 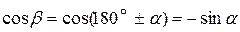 ; ;
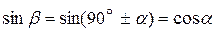 ; ; 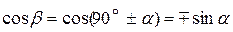 ; ; 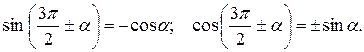
|
Векторы
Основные понятия. Многие физические величины характеризуются одним параметром – модулем. Например, известно расстояние, которое прошел студент (допустим, он прошел 17 км) – при этом все равно, в каком направлении он гулял, но известна температура воздуха в день его прогулки, например, 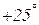 . Такие величины, как расстояние между точками и температура, называют скалярными величинами. Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 5 (км) к северо-востоку от пункта В, то недостаточно направить студента, указав расстояние в 5 (км) для того, чтобы он достиг пункт В. Необходимо задать направление движения. Комбинация модуля и направления физической величины называется векторной величиной, или просто вектором.
. Такие величины, как расстояние между точками и температура, называют скалярными величинами. Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 5 (км) к северо-востоку от пункта В, то недостаточно направить студента, указав расстояние в 5 (км) для того, чтобы он достиг пункт В. Необходимо задать направление движения. Комбинация модуля и направления физической величины называется векторной величиной, или просто вектором.
Важность понимания различий между векторными и скалярными величинами состоит в том, что для этих величин разные правила сложения, вычитания и умножения. Для скалярных величин эти правила прописаны в алгебре, для векторных величин – в векторной алгебре. Например, полное расстояние между пунктами А и В (по траектории движения 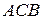 )вычисляется алгебраическим сложением (рис. 1.10, а):
)вычисляется алгебраическим сложением (рис. 1.10, а):
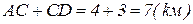
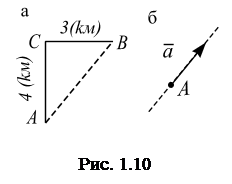 а полное перемещениевычисляется расстояниеммежду пунктами А и В, котороеравно
а полное перемещениевычисляется расстояниеммежду пунктами А и В, котороеравно
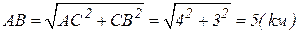 .
.
Вектор обозначается буквой с чертой (или стрелкой) над ней – 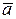 (
(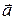 ) и изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины (рис. 1.10, б). Вектор характеризуется точкой приложения (точка А), модулем
) и изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины (рис. 1.10, б). Вектор характеризуется точкой приложения (точка А), модулем 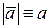 и линией действия – прямой, вдоль которой направлен вектор. Вектор, модуль которого
и линией действия – прямой, вдоль которой направлен вектор. Вектор, модуль которого 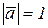 , называется единичным вектором. Если направление единичного вектора совпадает с направлением вектора, единичный вектор называется ортом. Орты, направленные по осям
, называется единичным вектором. Если направление единичного вектора совпадает с направлением вектора, единичный вектор называется ортом. Орты, направленные по осям 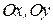 ,
, 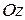 декартовой системы координат, обозначаются
декартовой системы координат, обозначаются 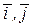 ,
, 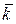 – единичные орты (рис. 1.11).
– единичные орты (рис. 1.11).
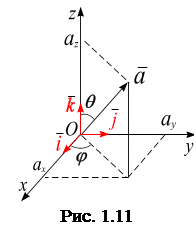 Проекция вектора на ось. Изобразим вектор
Проекция вектора на ось. Изобразим вектор 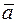 (рис. 11). Опустим перпендикуляры из начала А и конца В вектора на оси
(рис. 11). Опустим перпендикуляры из начала А и конца В вектора на оси 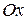 ,
, 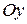 ,
, 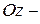 получим отрезки
получим отрезки 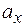 ,
, 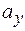 ,
, 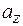 называемые проекциями вектора
называемые проекциями вектора 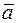 на оси
на оси 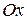 ,
, 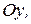
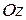 .
.
Каждый вектор 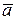 может бытьединственным образом разложен на сумму векторов, параллельных единичным ортам
может бытьединственным образом разложен на сумму векторов, параллельных единичным ортам 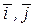 плоской системы:
плоской системы:
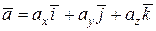 . (а)
. (а)
Скаляры 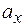 ,
, 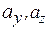 называются координатами вектора
называются координатами вектора 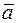 в системе
в системе 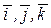 и обозначается это так
и обозначается это так
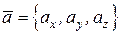 . (б)
. (б)
Записи (а) и (б) равносильны.
Координаты вектора 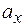 ,
, 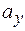 ,
, 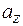 и модуль вычисляются по формулам:
и модуль вычисляются по формулам:
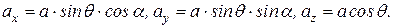 ,
, 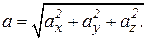
Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительным направлениями оси и направлением вектора (рис. 1.12):
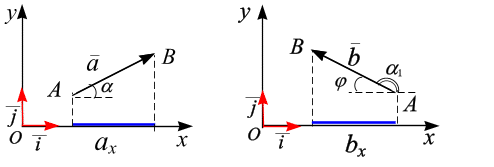
Рис. 1.12
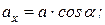
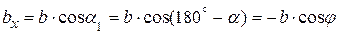 .
.
Линейные комбинации векторов. Сложение векторных величин производится по правилу параллелограмма: сумма двух векторов 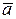 и
и 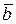 , приведенных к общему началу, есть третий вектор
, приведенных к общему началу, есть третий вектор 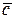 , длина которого равна длине параллелограмма, построенного на векторах
, длина которого равна длине параллелограмма, построенного на векторах 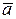 и
и 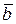 , а направлен вектор
, а направлен вектор 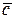 от точки A к точке B (рис. 1.13):
от точки A к точке B (рис. 1.13):
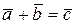 .
.
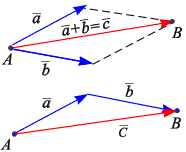 Рис. 1.13
Рис. 1.13
| Модуль вектора 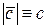 вычисляется по формуле вычисляется по формуле
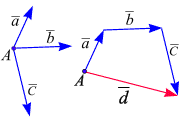
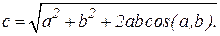 Силовой многоугольник. Суммируют несколько векторов построением векторного многоугольника. Слагаемые векторы путем параллельного переноса последовательно при-
Силовой многоугольник. Суммируют несколько векторов построением векторного многоугольника. Слагаемые векторы путем параллельного переноса последовательно при-
|
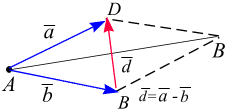
страивают один за другим так, что начало последующего вектора совпадает с концом предыдущего, тогда вектор, замыкающий полученный многоугольник является суммой заданных слагаемых, причём его начало совпадает с началом первого из слагаемых векторов, а конец – с концом последнего (рис. 1.14, а). Разность двух векторов. Разностью векторов 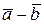 называется векторов
называется векторов 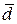 (диагональ BD) такой, что сумма векторов
(диагональ BD) такой, что сумма векторов 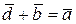
(рис. 1.14, б):
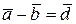 .
.
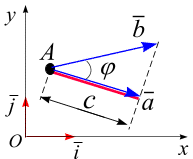
Скалярное умножение векторов. Скалярным умножением векторов 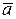 и
и 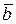 (обозначается
(обозначается 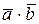 ) называется скаляр, определяемый равенством
) называется скаляр, определяемый равенством
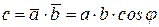 ,
,
где угол 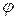 – угол между векторами
– угол между векторами 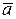 и
и 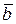 , приведенных к общему началу (рис. 14, в).
, приведенных к общему началу (рис. 14, в).
Если заданы векторы 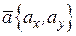 ,
, 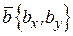 то скалярное произведение этих векторов вычисляется по формуле
то скалярное произведение этих векторов вычисляется по формуле
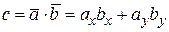 .
.
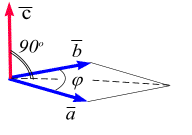
Векторное умножение векторов. Векторным произведением векторов 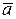 и
и 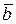 (обозначается
(обозначается 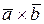 ) называется вектор
) называется вектор 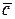 , длина которого равна
, длина которого равна 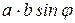 (т.е. площади параллелограмма, построенного на векторах, как на сторонах) и который направлен перпендикулярно плоскости расположения векторов
(т.е. площади параллелограмма, построенного на векторах, как на сторонах) и который направлен перпендикулярно плоскости расположения векторов 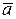 и
и 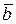 (рис. 1.14. г) Если векторы
(рис. 1.14. г) Если векторы 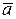 ,
, 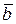 ,
, 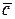 заданы декартовыми прямоугольными координатами:
заданы декартовыми прямоугольными координатами: 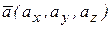 ,
, 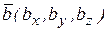 ,
, 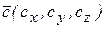 , то векторное произведение вычисляется по формуле
, то векторное произведение вычисляется по формуле
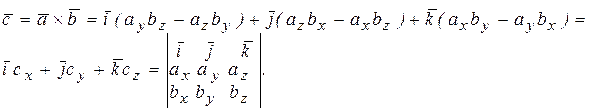
В механике разделяют три типа векторов: свободный, скользящий и связанный.
Свободными векторами представляются физические величины, не изменяющиеся при переходе от одной точки пространства к любой другой. Такие векторы характеризуют физические величины во всем исследуемом пространстве.
Скользящие векторы представляют собой векторные физические величины, остающиеся неизменными вдоль линии действия вектора. Они изменяются при переходе к другой точке пространства, не лежащей на линии действия.
Закрепленные векторы представляют собой векторные физические величины только в данной точке пространства. В других точках пространства они либо имеют другое значение, либо вообще теряют смысл.
§ 1.5. Радиус–вектор
Положение точки А на траектории в пространстве удобно характеризовать радиус–вектором. Для построения радиус-вектора выберем неподвижную точку 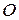 в евклидовом пространстве. Проведем через неподвижную точку
в евклидовом пространстве. Проведем через неподвижную точку 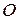 произвольно ось
произвольно ось 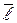 . Если каждому значению скалярного аргумента t поставить в соответствие вектор
. Если каждому значению скалярного аргумента t поставить в соответствие вектор 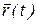 (расстояние между точкой
(расстояние между точкой 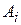 на траектории и полюсом О фиксируется
на траектории и полюсом О фиксируется 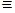 модулем
модулем 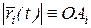 , направление прямой
, направление прямой 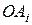 фиксируется углом
фиксируется углом 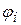 ) то функция
) то функция 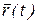 будет называться радиус–вектором скалярного аргумента (рис. 15, а). Если начало вектора
будет называться радиус–вектором скалярного аргумента (рис. 15, а). Если начало вектора 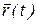 (ра
(ра 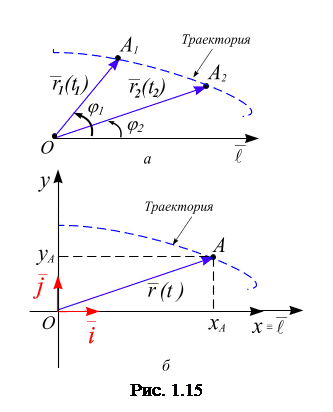 диус-вектора) находится в точке О, то конец радиус-вектора
диус-вектора) находится в точке О, то конец радиус-вектора 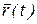 опишет пространственную кривую, которую называют годографом (записыватель пути) векторной функции (рис. 15, а). Если t означает время, то
опишет пространственную кривую, которую называют годографом (записыватель пути) векторной функции (рис. 15, а). Если t означает время, то 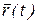 фиксирует положение материальной точки в пространстве в любой момент времени, т.е. характеризует движение материальной точки, а годограф радиус-вектора соответствует траектории движения точки.
фиксирует положение материальной точки в пространстве в любой момент времени, т.е. характеризует движение материальной точки, а годограф радиус-вектора соответствует траектории движения точки.
Пусть точка движется в плоскости 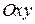 . Совместим с точкой
. Совместим с точкой 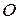 начало плоской декартовой системы, а ось
начало плоской декартовой системы, а ось 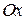 с осью
с осью 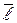 (рис. 1.15, б). В плоской декартовой системе координат радиус–вектор
(рис. 1.15, б). В плоской декартовой системе координат радиус–вектор 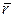 раскладывается по базисным векторам
раскладывается по базисным векторам 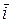 ,
, 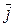 так (рис. 1.15, б)
так (рис. 1.15, б)
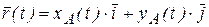 ,
,
причем компоненты 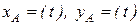 являются координатами точки А в прямоугольной системе координат.
являются координатами точки А в прямоугольной системе координат.
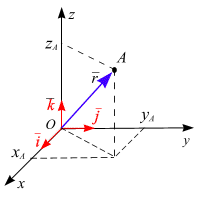 Рис. 1.16
Рис. 1.16
| Радиус–вектор 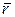 можно разложить по базисным векторам можно разложить по базисным векторам 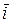 , , 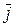 , , 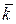 прямоугольной пространственной системы координат, то (рис.1.16) прямоугольной пространственной системы координат, то (рис.1.16)
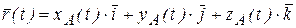 ,
причем компоненты ,
причем компоненты 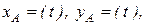 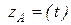 являются координатами точки А в прямоугольной системе координат. являются координатами точки А в прямоугольной системе координат.
|
Правила интегрирования
Неопределенный интеграл:
 , где
, где  ,
,  .
.
Свойства неопределенного интеграла:
 ;
;  .
.
Свойство линейности:
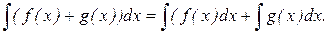

Метод замены переменного:
 , где
, где  .
.
Метод интегрирования по частям
 .
.
Свойства определенного интеграла:
 ;
;  ;
;
 ;
; 
Формула Ньютона – Лейбница:
 .
.
Таблица интегралов
Продолжение таблицы интегралов
§ 1.7. Понятие об абсолютно твердом теле и его
Степенях свободы
Важным понятием в механике является число параметров, полностью определяющих положение всех точек рассматриваемой системы, в частности твердого тела. Эти параметры носят название степеней свободы.
Свободным называется тело на перемещения точек которого не наложено никаких ограничений. Вычислим количество степеней свободы твердого тела в плоскости и пространстве.
Число независимых параметров, определяющих перемещение тела (точек тела) на плоскости или в пространстве называется числом его степеней свободы.
Плоскость. Положение точки на плоскости в системе координат  определяется двумя независимости параметрами (координатами) –
определяется двумя независимости параметрами (координатами) – 
(рис. 1.19, а), т.е. точка может независимо перемещаться в двух ортогональных направлениях  и
и 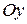 , следовательно, точка имеет две степени свободы.
, следовательно, точка имеет две степени свободы.

Рис. 1.19
Положение твердого тела характеризовать двумя параметрами не получится, необходимо зафиксировать еще одну точку, тогда положение твердого тела на плоскости будет определено четырьмя параметрами – координатами двух точек –  и
и  (рис. 1.19, б).
(рис. 1.19, б).
Предположим, что при движении или взаимодействии с другими телами твердое тело не меняет своей геометрической формы, тогда расстояние между точками А и В будет оставаться неизменным:

Такие твердые тела называют абсолютно твердыми телами. В теоретической механике реальные тела моделируются абсолютно твердыми телами.
| Абсолютно твердым телом (или неизменяемой механической системой) называют твердое тело, расстояние между любыми точками которого не меняется при его движении и взаимодействии с другими телами.
|
Тогда четыре координаты  ,
,  , определяющие положение абсолютно твердого тела связаны между собой теоремой Пифагора:
, определяющие положение абсолютно твердого тела связаны между собой теоремой Пифагора:
 . (1.5)
. (1.5)
Это уравнение принято называть уравнением связи. Тогда из четырех координат  ,
,  , независимые только три:
, независимые только три:
4-координаты – 1 уравнение связи  3 независимых координаты.
3 независимых координаты.
Поэтому движение абсолютно твердого тела в плоскости должно описываться тремя независимыми параметрами. За независимые параметры выбирают координаты любой точки А –  , (часто центра тяжести тела) и угол
, (часто центра тяжести тела) и угол  , который образует жестко связанная с телом прямая АВ и положительным направлением оси
, который образует жестко связанная с телом прямая АВ и положительным направлением оси 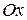 (рис. 1.19, б). Итак, положение абсолютно твердого тела в плоскости будет определяться тремя независимыми параметрами –
(рис. 1.19, б). Итак, положение абсолютно твердого тела в плоскости будет определяться тремя независимыми параметрами –  ,
,  и, следовательно, твердое тело при движении в плоскости будет иметь три степени свободы: тело может перемещаться вдоль каждой из осей и вращаться вокруг точки А. Точку А называют полюсом.
и, следовательно, твердое тело при движении в плоскости будет иметь три степени свободы: тело может перемещаться вдоль каждой из осей и вращаться вокруг точки А. Точку А называют полюсом.
| Число независимых перемещений тела определяет число его степеней
свободы
|
Абсолютно твердое тело в плоскости имеет три степени свободы.
Пространство. Одна свободная точка в пространстве имеет три степени свободы. Рассмотрим свободное абсолютно твердое тело в пространстве (рис. 1.19). Положение твердого тела характеризовать двумя точками А и В в пространстве не получится, потому, что тело может вращаться вокруг прямой АВ, при этом координаты точек А и В меняться не будут. Необходимо зафиксировать еще одну точку, тогда положение тела в пространстве будет определяется заданием координат трех его точек, не лежащих на одной прямой ––  ,
,  ,
,  . Положение тела в пространстве в декартовой системе координат будет характеризуется девятью параметрами. Поскольку взаимное расположение точек А, В и С абсолютно твердого теласохраняется (рис. 1.20), девять координат связаны между собой тремя уравнениями связи:
. Положение тела в пространстве в декартовой системе координат будет характеризуется девятью параметрами. Поскольку взаимное расположение точек А, В и С абсолютно твердого теласохраняется (рис. 1.20), девять координат связаны между собой тремя уравнениями связи:
 – расстояние АВ;
– расстояние АВ;
 – расстояние АС; (1.6)
– расстояние АС; (1.6)
 – расстояние ВС.
– расстояние ВС.

| На девять координат наложено три уравнения связи, следовательно, независимых координат остается только шесть, т.е. абсолютно твердое тело в пространстве имеет шесть степеней свободы: тело может независимо перемещаться вдоль каждой из осей и вращаться вокруг
|
| Рис. 1.20
|
каждой оси. За независимые параметры выбирают координаты полюса А –  и углы поворота плоскости АВС вокруг каждой из осей. т.е. точка может независимо перемещаться в трех ортогональных направлениях
и углы поворота плоскости АВС вокруг каждой из осей. т.е. точка может независимо перемещаться в трех ортогональных направлениях  .
.
Если при движении или взаимодействии с другими телами твердое тело меняет свою геометрическую форму (деформируется), тогда расстояние между двумя точками не будет оставаться неизменным, т.е. координаты точек  не связаны между собой. В этом случае будем говорить о деформируемом твердом теле.
не связаны между собой. В этом случае будем говорить о деформируемом твердом теле.
МОДУЛЬ I
ВВЕДЕНИЕ
Механика – дисциплина, при изучении которой студенты в первую очередь могут проследить функционирование математической модели и сопоставить ее с реальным процессом. Апробация теории позволяет закрепить знания, полученные при изучении математического анализа, алгебры, аналитической геометрии и вычислительной математики. Причем все эти дисциплины используются во взаимосвязи. В их кругу теоретическая механика занимает особое место.
Это наука о законах механического движения и взаимодействия материальных тел. Имея технические корни, она развивается в теснейшей связи с курсом механики деформируемого твердого тела (и особенно с одним из ее разделов – сопротивлением материалов).
Для изучения курса важно иметь соответствующую математическую подготовку. Во всех разделах широко применяется векторная алгебра. Необходимо уметь вычислять проекции векторов на координатные оси, геометрически и аналитически находить сумму векторов, скалярное и векторное произведения, а также знать их свойства и правила дифференцирования.
Кроме того, важно уяснить сущность каждого излагаемого вопроса. Особое внимание следует уделить приобретению навыков решения задач.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
При изучении учебного курса «Теоретическая механика» студент знакомится с математическими моделями реальных явлений и существующими методами расчета, которые базируются на знаниях, полученных при изучении аналитической геометрии и линейной алгебры, векторной алгебры, высшей алгебры, основ математического анализа (табл. 1).
Табл. 1.
| Наименование дисциплины
| Раздел
| Тема
|
| Математика
| Аналитическая геометрия и линейная алгебра
| Алгебраические преобразования, решение алгебраических уравнений первого и второго порядка, Евклидова геометрия, тригонометрия, функции и графики аналитических и трансцендентных функций.
|
| Векторная алгебра
| Системы координат, преобразование систем координат, понятие вектора и линейные операции над ним, проекции векторов на оси, геометрическое и аналитическое сложение векторов, скалярное и векторное произведения векторов, решение векторных уравнений, кривые второго порядка, параметрическое задание функций.
|
| Высшая алгебра
| Системы линейных уравнений, определители, квадратичные формы, Евклидовы пространства, вычисление корней многочленов.
|
| Основы математического анализа
| Дифференцирование функций, экстремумы функций, геометрические приложения производных, неопределенный и определенный интегралы, дифференциальные уравнения, ряды.
|
Основным документом, определяющим необходимый объём знаний студентов, является программа курса, составленная на основе государственного образовательного стандарта высшего профессионального образования.
Процесс овладения студентами определенных знаний и навыков, складывается из самостоятельного изучения соответствующих разделов курса по учебникам, самостоятельного выполнения контрольных работ. Контрольная работа оформляется на бумаге формата А4, согласно правилам черчения. Оформление титульного листа контрольной работы показано на рис.1
При оформлении контрольной работы необходимо выписать для заданного варианта полное условие с числовыми данными, написать текст задания, составить аккуратный чертеж с соблюдением масштаба и показать на нем все размеры в числах. Каждый студент обязан защитить контрольные работы.
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО КГПУ им. В.П. Астафьева
Кафедра «Технология и предпринимательство»
Контрольная работа №
по кинематике
(модуль 1)
тема задания_________________
____________________________
выполнил студент (ка)_________гр.
Ф. И. О. _______________________
Проверил______________________
«___» __________________ 200 г.
Красноярск
201 г.
|
Рис. 1.
Каждый этап решения задачи в контрольной работе должен быть озаглавлен. При выполнении расчетов сначала записывается формула, затем в нее подставляются исходные данные с размерностями системы Си и подсчитывается результат. Например:

Решение должно сопровождаться краткими, последовательными и грамотными, без сокращения слов, объяснениями и чертежами, на которых должны быть показаны все размеры в числах. Необходимо указывать единицы измерения (размерность) всех полученных результатов. Задание, выполненное небрежно, без соблюдения всех перечисленных требований, не принимается.
Защита контрольных работ производится во время сессии, в сроки, установленные графиком учебного процесса в следующем порядке:
· преподаватель проверяет готовые задания, указывает на ошибки, если они имеются и задает несколько вопросов по теме выполненного задания;
· для защиты задания студенту дается задача по этой теме в виде контрольной работы;
· задание не засчитывается, если студент не смог решить предложенную преподавателем задачу. Только после дополнительного изучения темы он может повторно защитить задание.
·
Прямоугольная декартова система координат
Содержание: общие методические указания Прямоугольная декартова система координат. Графики аналитических функций в декартовой системе координат. Элементы тригонометрии. Графики тригонометрических функций. Векторы. Радиус–вектор. Основы математического анализа. Понятие об абсолютно твердом теле и его степенях свободы. Инерциальная система отсчета.
Рене Декарт предложил задавать положение точек отрезка с помощью системы параллельных отрезков  и
и  , перпендикулярных к исходной прямой
, перпендикулярных к исходной прямой  (рис. 1.1, в). В дальнейшем была введена вторая ось, перпендикулярная первой. Система двух ортогональных осей получила название декартовой системой координат (рис. 1.1, в).
(рис. 1.1, в). В дальнейшем была введена вторая ось, перпендикулярная первой. Система двух ортогональных осей получила название декартовой системой координат (рис. 1.1, в).
Декартова плоская система координат задается двумя взаимно перпендикулярными





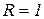 (рис. 1.7). Длина окружности круга единичного радиуса равна
(рис. 1.7). Длина окружности круга единичного радиуса равна 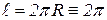 , откуда
, откуда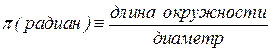
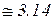
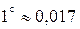 рад.
рад. 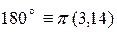 рад.;
рад.;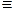
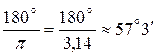 .
.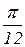
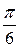
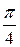
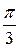
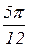
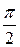
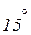
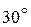
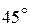
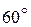
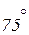
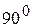
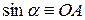
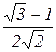
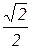
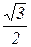
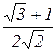
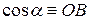
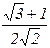
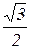
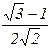
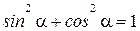 .
Функции двойного угла:
.
Функции двойного угла:
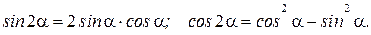 Формулы приведения:
Формулы приведения:
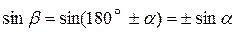 ;
; 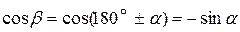 ;
;
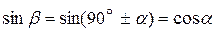 ;
; 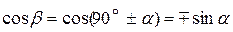 ;
; 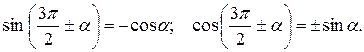
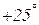 . Такие величины, как расстояние между точками и температура, называют скалярными величинами. Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 5 (км) к северо-востоку от пункта В, то недостаточно направить студента, указав расстояние в 5 (км) для того, чтобы он достиг пункт В. Необходимо задать направление движения. Комбинация модуля и направления физической величины называется векторной величиной, или просто вектором.
. Такие величины, как расстояние между точками и температура, называют скалярными величинами. Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 5 (км) к северо-востоку от пункта В, то недостаточно направить студента, указав расстояние в 5 (км) для того, чтобы он достиг пункт В. Необходимо задать направление движения. Комбинация модуля и направления физической величины называется векторной величиной, или просто вектором.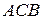 )вычисляется алгебраическим сложением (рис. 1.10, а):
)вычисляется алгебраическим сложением (рис. 1.10, а):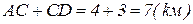
 а полное перемещениевычисляется расстояниеммежду пунктами А и В, котороеравно
а полное перемещениевычисляется расстояниеммежду пунктами А и В, котороеравно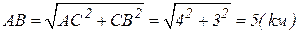 .
.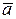 (
(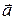 ) и изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины (рис. 1.10, б). Вектор характеризуется точкой приложения (точка А), модулем
) и изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины (рис. 1.10, б). Вектор характеризуется точкой приложения (точка А), модулем 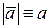 и линией действия – прямой, вдоль которой направлен вектор. Вектор, модуль которого
и линией действия – прямой, вдоль которой направлен вектор. Вектор, модуль которого 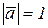 , называется единичным вектором. Если направление единичного вектора совпадает с направлением вектора, единичный вектор называется ортом. Орты, направленные по осям
, называется единичным вектором. Если направление единичного вектора совпадает с направлением вектора, единичный вектор называется ортом. Орты, направленные по осям 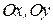 ,
, 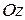 декартовой системы координат, обозначаются
декартовой системы координат, обозначаются 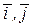 ,
, 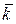 – единичные орты (рис. 1.11).
– единичные орты (рис. 1.11). Проекция вектора на ось. Изобразим вектор
Проекция вектора на ось. Изобразим вектор 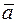 (рис. 11). Опустим перпендикуляры из начала А и конца В вектора на оси
(рис. 11). Опустим перпендикуляры из начала А и конца В вектора на оси 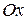 ,
, 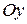 ,
, 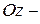 получим отрезки
получим отрезки 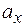 ,
, 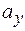 ,
, 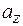 называемые проекциями вектора
называемые проекциями вектора 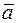 на оси
на оси 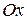 ,
, 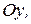
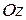 .
.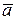 может бытьединственным образом разложен на сумму векторов, параллельных единичным ортам
может бытьединственным образом разложен на сумму векторов, параллельных единичным ортам 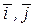 плоской системы:
плоской системы: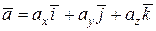 . (а)
. (а)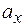 ,
, 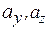 называются координатами вектора
называются координатами вектора 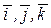 и обозначается это так
и обозначается это так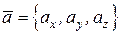 . (б)
. (б)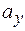 ,
, 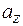 и модуль вычисляются по формулам:
и модуль вычисляются по формулам: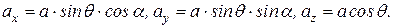 ,
, 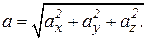

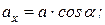
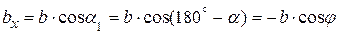 .
.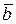 , приведенных к общему началу, есть третий вектор
, приведенных к общему началу, есть третий вектор 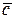 , длина которого равна длине параллелограмма, построенного на векторах
, длина которого равна длине параллелограмма, построенного на векторах 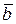 , а направлен вектор
, а направлен вектор 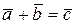 .
. Рис. 1.13
Рис. 1.13
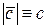 вычисляется по формуле
вычисляется по формуле
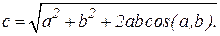 Силовой многоугольник. Суммируют несколько векторов построением векторного многоугольника. Слагаемые векторы путем параллельного переноса последовательно при-
Силовой многоугольник. Суммируют несколько векторов построением векторного многоугольника. Слагаемые векторы путем параллельного переноса последовательно при-
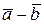 называется векторов
называется векторов 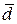 (диагональ BD) такой, что сумма векторов
(диагональ BD) такой, что сумма векторов 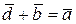
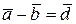 .
.
 г
г
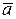 и
и 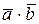 ) называется скаляр, определяемый равенством
) называется скаляр, определяемый равенством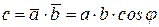 ,
,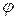 – угол между векторами
– угол между векторами 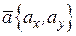 ,
, 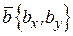 то скалярное произведение этих векторов вычисляется по формуле
то скалярное произведение этих векторов вычисляется по формуле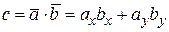 .
.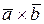 ) называется вектор
) называется вектор 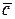 , длина которого равна
, длина которого равна 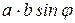 (т.е. площади параллелограмма, построенного на векторах, как на сторонах) и который направлен перпендикулярно плоскости расположения векторов
(т.е. площади параллелограмма, построенного на векторах, как на сторонах) и который направлен перпендикулярно плоскости расположения векторов 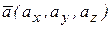 ,
, 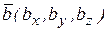 ,
, 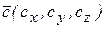 , то векторное произведение вычисляется по формуле
, то векторное произведение вычисляется по формуле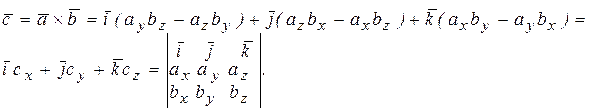
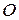 в евклидовом пространстве. Проведем через неподвижную точку
в евклидовом пространстве. Проведем через неподвижную точку 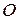 произвольно ось
произвольно ось 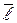 . Если каждому значению скалярного аргумента t поставить в соответствие вектор
. Если каждому значению скалярного аргумента t поставить в соответствие вектор 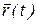 (расстояние между точкой
(расстояние между точкой 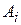 на траектории и полюсом О фиксируется
на траектории и полюсом О фиксируется 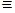 модулем
модулем 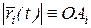 , направление прямой
, направление прямой 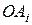 фиксируется углом
фиксируется углом 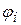 ) то функция
) то функция 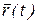 будет называться радиус–вектором скалярного аргумента (рис. 15, а). Если начало вектора
будет называться радиус–вектором скалярного аргумента (рис. 15, а). Если начало вектора  диус-вектора) находится в точке О, то конец радиус-вектора
диус-вектора) находится в точке О, то конец радиус-вектора 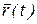 опишет пространственную кривую, которую называют годографом (записыватель пути) векторной функции (рис. 15, а). Если t означает время, то
опишет пространственную кривую, которую называют годографом (записыватель пути) векторной функции (рис. 15, а). Если t означает время, то 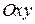 . Совместим с точкой
. Совместим с точкой 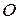 начало плоской декартовой системы, а ось
начало плоской декартовой системы, а ось 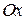 с осью
с осью 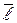 (рис. 1.15, б). В плоской декартовой системе координат радиус–вектор
(рис. 1.15, б). В плоской декартовой системе координат радиус–вектор 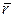 раскладывается по базисным векторам
раскладывается по базисным векторам 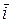 ,
, 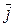 так (рис. 1.15, б)
так (рис. 1.15, б)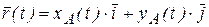 ,
,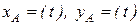 являются координатами точки А в прямоугольной системе координат.
являются координатами точки А в прямоугольной системе координат. Рис. 1.16
Рис. 1.16
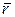 можно разложить по базисным векторам
можно разложить по базисным векторам 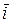 ,
, 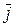 ,
, 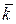 прямоугольной пространственной системы координат, то (рис.1.16)
прямоугольной пространственной системы координат, то (рис.1.16)
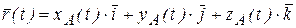 ,
причем компоненты
,
причем компоненты 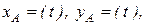
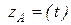 являются координатами точки А в прямоугольной системе координат.
являются координатами точки А в прямоугольной системе координат.
 , где
, где  ,
,  .
. ;
;  .
.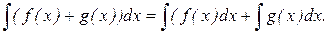

 , где
, где  .
. .
. ;
;  ;
; ;
; 
 .
.










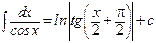

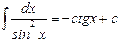


 определяется двумя независимости параметрами (координатами) –
определяется двумя независимости параметрами (координатами) – 
 и
и 
 и
и  (рис. 1.19, б).
(рис. 1.19, б).
 ,
,  , определяющие положение абсолютно твердого тела связаны между собой теоремой Пифагора:
, определяющие положение абсолютно твердого тела связаны между собой теоремой Пифагора: . (1.5)
. (1.5) 3 независимых координаты.
3 независимых координаты. , (часто центра тяжести тела) и угол
, (часто центра тяжести тела) и угол  , который образует жестко связанная с телом прямая АВ и положительным направлением оси
, который образует жестко связанная с телом прямая АВ и положительным направлением оси 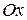 (рис. 1.19, б). Итак, положение абсолютно твердого тела в плоскости будет определяться тремя независимыми параметрами –
(рис. 1.19, б). Итак, положение абсолютно твердого тела в плоскости будет определяться тремя независимыми параметрами –  ,
,  и, следовательно, твердое тело при движении в плоскости будет иметь три степени свободы: тело может перемещаться вдоль каждой из осей и вращаться вокруг точки А. Точку А называют полюсом.
и, следовательно, твердое тело при движении в плоскости будет иметь три степени свободы: тело может перемещаться вдоль каждой из осей и вращаться вокруг точки А. Точку А называют полюсом. ,
,  ,
,  . Положение тела в пространстве в декартовой системе координат будет характеризуется девятью параметрами. Поскольку взаимное расположение точек А, В и С абсолютно твердого теласохраняется (рис. 1.20), девять координат связаны между собой тремя уравнениями связи:
. Положение тела в пространстве в декартовой системе координат будет характеризуется девятью параметрами. Поскольку взаимное расположение точек А, В и С абсолютно твердого теласохраняется (рис. 1.20), девять координат связаны между собой тремя уравнениями связи: – расстояние АВ;
– расстояние АВ; – расстояние АС; (1.6)
– расстояние АС; (1.6) – расстояние ВС.
– расстояние ВС.
 и углы поворота плоскости АВС вокруг каждой из осей. т.е. точка может независимо перемещаться в трех ортогональных направлениях
и углы поворота плоскости АВС вокруг каждой из осей. т.е. точка может независимо перемещаться в трех ортогональных направлениях  .
. не связаны между собой. В этом случае будем говорить о деформируемом твердом теле.
не связаны между собой. В этом случае будем говорить о деформируемом твердом теле. Рис. 1.1
Рис. 1.1 , где точка С лежит между точками А и В (рис. 1.1, а). Но если два расстояния взяты не на одной прямой, то их сумма не может быть определена однозначно без дополнительных условий. Если
, где точка С лежит между точками А и В (рис. 1.1, а). Но если два расстояния взяты не на одной прямой, то их сумма не может быть определена однозначно без дополнительных условий. Если  – три точки, то расстояние
– три точки, то расстояние  определяется не только расстояниями
определяется не только расстояниями  и
и  , т.е.
, т.е.  (рис. 1.1, б).
(рис. 1.1, б).  и
и  , перпендикулярных к исходной прямой
, перпендикулярных к исходной прямой  (рис. 1.1, в). В дальнейшем была введена вторая ось, перпендикулярная первой. Система двух ортогональных осей получила название декартовой системой координат (рис. 1.1, в).
(рис. 1.1, в). В дальнейшем была введена вторая ось, перпендикулярная первой. Система двух ортогональных осей получила название декартовой системой координат (рис. 1.1, в).


