При построении тригонометрических функций мы используем радианную меру измерения углов.Тогда функция 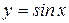 представляется графиком (рис. 1.8). Эта кривая называется синусоидой.
представляется графиком (рис. 1.8). Эта кривая называется синусоидой.
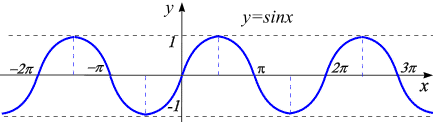
Рис. 1.8
График функции 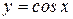 представлен на рис. 1.9; это кривая называется также синусоида, полученная в результате перемещения графика
представлен на рис. 1.9; это кривая называется также синусоида, полученная в результате перемещения графика 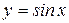 вдоль оси
вдоль оси 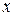 влево на
влево на  /2.
/2.
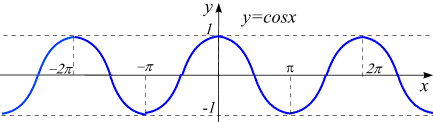
Рис. 1.9
Характеристики и свойства тригонометрических функций:
– область определения: 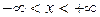 ;область значений:
;область значений: 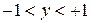 ;
;
– функции периодические, их период равен 2  ;
;
– функции ограниченные (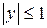 ), всюду непрерывные.
), всюду непрерывные.
Векторы
Основные понятия. Многие физические величины характеризуются одним параметром – модулем. Например, известно расстояние, которое прошел студент (допустим, он прошел 17 км) – при этом все равно, в каком направлении он гулял, но известна температура воздуха в день его прогулки, например, 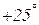 . Такие величины, как расстояние между точками и температура, называют скалярными величинами. Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 5 (км) к северо-востоку от пункта В, то недостаточно направить студента, указав расстояние в 5 (км) для того, чтобы он достиг пункт В. Необходимо задать направление движения. Комбинация модуля и направления физической величины называется векторной величиной, или просто вектором.
. Такие величины, как расстояние между точками и температура, называют скалярными величинами. Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 5 (км) к северо-востоку от пункта В, то недостаточно направить студента, указав расстояние в 5 (км) для того, чтобы он достиг пункт В. Необходимо задать направление движения. Комбинация модуля и направления физической величины называется векторной величиной, или просто вектором.
Важность понимания различий между векторными и скалярными величинами состоит в том, что для этих величин разные правила сложения, вычитания и умножения. Для скалярных величин эти правила прописаны в алгебре, для векторных величин – в векторной алгебре. Например, полное расстояние между пунктами А и В (по траектории движения 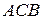 )вычисляется алгебраическим сложением (рис. 1.10, а):
)вычисляется алгебраическим сложением (рис. 1.10, а):
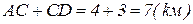
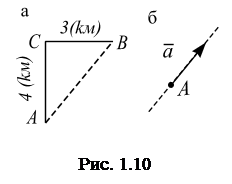 а полное перемещениевычисляется расстояниеммежду пунктами А и В, котороеравно
а полное перемещениевычисляется расстояниеммежду пунктами А и В, котороеравно
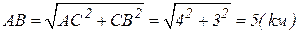 .
.
Вектор обозначается буквой с чертой (или стрелкой) над ней – 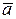 (
(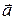 ) и изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины (рис. 1.10, б). Вектор характеризуется точкой приложения (точка А), модулем
) и изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины (рис. 1.10, б). Вектор характеризуется точкой приложения (точка А), модулем 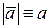 и линией действия – прямой, вдоль которой направлен вектор. Вектор, модуль которого
и линией действия – прямой, вдоль которой направлен вектор. Вектор, модуль которого 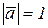 , называется единичным вектором. Если направление единичного вектора совпадает с направлением вектора, единичный вектор называется ортом. Орты, направленные по осям
, называется единичным вектором. Если направление единичного вектора совпадает с направлением вектора, единичный вектор называется ортом. Орты, направленные по осям 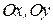 ,
, 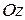 декартовой системы координат, обозначаются
декартовой системы координат, обозначаются 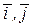 ,
, 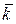 – единичные орты (рис. 1.11).
– единичные орты (рис. 1.11).
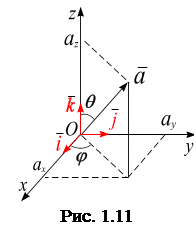 Проекция вектора на ось. Изобразим вектор
Проекция вектора на ось. Изобразим вектор 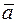 (рис. 11). Опустим перпендикуляры из начала А и конца В вектора на оси
(рис. 11). Опустим перпендикуляры из начала А и конца В вектора на оси 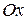 ,
, 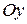 ,
, 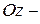 получим отрезки
получим отрезки 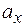 ,
, 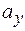 ,
, 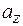 называемые проекциями вектора
называемые проекциями вектора 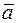 на оси
на оси 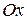 ,
, 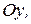
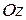 .
.
Каждый вектор 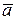 может бытьединственным образом разложен на сумму векторов, параллельных единичным ортам
может бытьединственным образом разложен на сумму векторов, параллельных единичным ортам 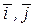 плоской системы:
плоской системы:
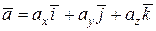 . (а)
. (а)
Скаляры 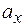 ,
, 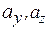 называются координатами вектора
называются координатами вектора 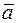 в системе
в системе 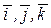 и обозначается это так
и обозначается это так
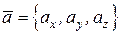 . (б)
. (б)
Записи (а) и (б) равносильны.
Координаты вектора 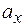 ,
, 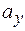 ,
, 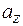 и модуль вычисляются по формулам:
и модуль вычисляются по формулам:
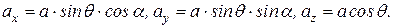 ,
, 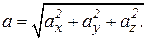
Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительным направлениями оси и направлением вектора (рис. 1.12):
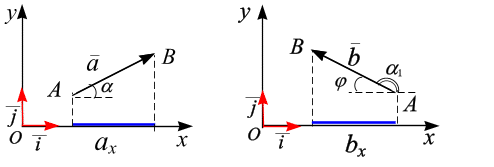
Рис. 1.12
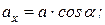
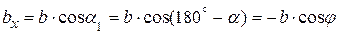 .
.
Линейные комбинации векторов. Сложение векторных величин производится по правилу параллелограмма: сумма двух векторов 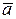 и
и 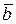 , приведенных к общему началу, есть третий вектор
, приведенных к общему началу, есть третий вектор 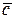 , длина которого равна длине параллелограмма, построенного на векторах
, длина которого равна длине параллелограмма, построенного на векторах 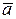 и
и 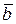 , а направлен вектор
, а направлен вектор 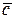 от точки A к точке B (рис. 1.13):
от точки A к точке B (рис. 1.13):
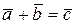 .
.
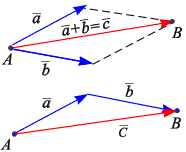 Рис. 1.13
Рис. 1.13
| Модуль вектора 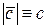 вычисляется по формуле вычисляется по формуле
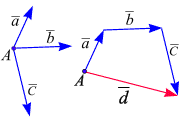
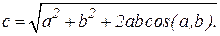 Силовой многоугольник. Суммируют несколько векторов построением векторного многоугольника. Слагаемые векторы путем параллельного переноса последовательно при-
Силовой многоугольник. Суммируют несколько векторов построением векторного многоугольника. Слагаемые векторы путем параллельного переноса последовательно при-
|
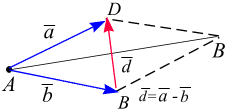
страивают один за другим так, что начало последующего вектора совпадает с концом предыдущего, тогда вектор, замыкающий полученный многоугольник является суммой заданных слагаемых, причём его начало совпадает с началом первого из слагаемых векторов, а конец – с концом последнего (рис. 1.14, а). Разность двух векторов. Разностью векторов 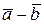 называется векторов
называется векторов 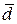 (диагональ BD) такой, что сумма векторов
(диагональ BD) такой, что сумма векторов 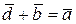
(рис. 1.14, б):
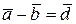 .
.
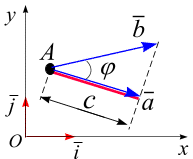
Скалярное умножение векторов. Скалярным умножением векторов 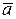 и
и 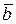 (обозначается
(обозначается 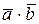 ) называется скаляр, определяемый равенством
) называется скаляр, определяемый равенством
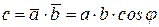 ,
,
где угол 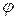 – угол между векторами
– угол между векторами 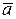 и
и 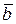 , приведенных к общему началу (рис. 14, в).
, приведенных к общему началу (рис. 14, в).
Если заданы векторы 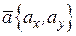 ,
, 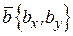 то скалярное произведение этих векторов вычисляется по формуле
то скалярное произведение этих векторов вычисляется по формуле
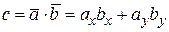 .
.
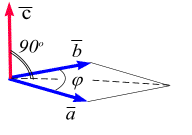
Векторное умножение векторов. Векторным произведением векторов 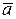 и
и 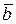 (обозначается
(обозначается 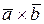 ) называется вектор
) называется вектор 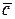 , длина которого равна
, длина которого равна 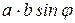 (т.е. площади параллелограмма, построенного на векторах, как на сторонах) и который направлен перпендикулярно плоскости расположения векторов
(т.е. площади параллелограмма, построенного на векторах, как на сторонах) и который направлен перпендикулярно плоскости расположения векторов 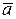 и
и 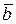 (рис. 1.14. г) Если векторы
(рис. 1.14. г) Если векторы 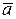 ,
, 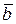 ,
, 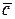 заданы декартовыми прямоугольными координатами:
заданы декартовыми прямоугольными координатами: 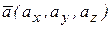 ,
, 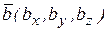 ,
, 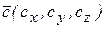 , то векторное произведение вычисляется по формуле
, то векторное произведение вычисляется по формуле
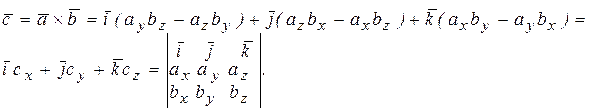
В механике разделяют три типа векторов: свободный, скользящий и связанный.
Свободными векторами представляются физические величины, не изменяющиеся при переходе от одной точки пространства к любой другой. Такие векторы характеризуют физические величины во всем исследуемом пространстве.
Скользящие векторы представляют собой векторные физические величины, остающиеся неизменными вдоль линии действия вектора. Они изменяются при переходе к другой точке пространства, не лежащей на линии действия.
Закрепленные векторы представляют собой векторные физические величины только в данной точке пространства. В других точках пространства они либо имеют другое значение, либо вообще теряют смысл.
§ 1.5. Радиус–вектор
Положение точки А на траектории в пространстве удобно характеризовать радиус–вектором. Для построения радиус-вектора выберем неподвижную точку 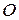 в евклидовом пространстве. Проведем через неподвижную точку
в евклидовом пространстве. Проведем через неподвижную точку 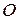 произвольно ось
произвольно ось 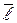 . Если каждому значению скалярного аргумента t поставить в соответствие вектор
. Если каждому значению скалярного аргумента t поставить в соответствие вектор 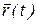 (расстояние между точкой
(расстояние между точкой 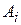 на траектории и полюсом О фиксируется
на траектории и полюсом О фиксируется 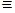 модулем
модулем 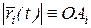 , направление прямой
, направление прямой 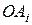 фиксируется углом
фиксируется углом 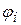 ) то функция
) то функция 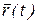 будет называться радиус–вектором скалярного аргумента (рис. 15, а). Если начало вектора
будет называться радиус–вектором скалярного аргумента (рис. 15, а). Если начало вектора 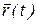 (ра
(ра 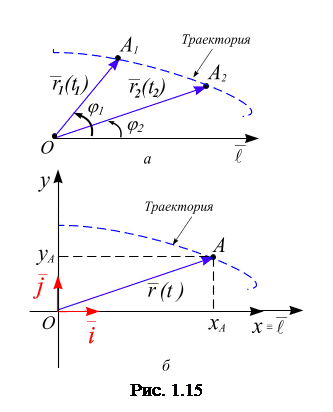 диус-вектора) находится в точке О, то конец радиус-вектора
диус-вектора) находится в точке О, то конец радиус-вектора 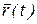 опишет пространственную кривую, которую называют годографом (записыватель пути) векторной функции (рис. 15, а). Если t означает время, то
опишет пространственную кривую, которую называют годографом (записыватель пути) векторной функции (рис. 15, а). Если t означает время, то 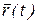 фиксирует положение материальной точки в пространстве в любой момент времени, т.е. характеризует движение материальной точки, а годограф радиус-вектора соответствует траектории движения точки.
фиксирует положение материальной точки в пространстве в любой момент времени, т.е. характеризует движение материальной точки, а годограф радиус-вектора соответствует траектории движения точки.
Пусть точка движется в плоскости 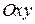 . Совместим с точкой
. Совместим с точкой 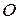 начало плоской декартовой системы, а ось
начало плоской декартовой системы, а ось 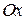 с осью
с осью 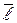 (рис. 1.15, б). В плоской декартовой системе координат радиус–вектор
(рис. 1.15, б). В плоской декартовой системе координат радиус–вектор 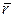 раскладывается по базисным векторам
раскладывается по базисным векторам 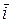 ,
, 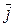 так (рис. 1.15, б)
так (рис. 1.15, б)
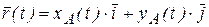 ,
,
причем компоненты 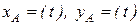 являются координатами точки А в прямоугольной системе координат.
являются координатами точки А в прямоугольной системе координат.
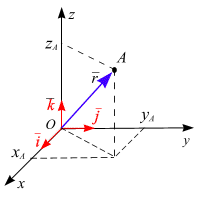 Рис. 1.16
Рис. 1.16
| Радиус–вектор 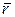 можно разложить по базисным векторам можно разложить по базисным векторам 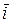 , , 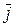 , , 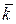 прямоугольной пространственной системы координат, то (рис.1.16) прямоугольной пространственной системы координат, то (рис.1.16)
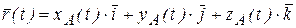 ,
причем компоненты ,
причем компоненты 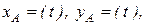 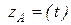 являются координатами точки А в прямоугольной системе координат. являются координатами точки А в прямоугольной системе координат.
|



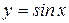 представляется графиком (рис. 1.8). Эта кривая называется синусоидой.
представляется графиком (рис. 1.8). Эта кривая называется синусоидой.
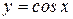 представлен на рис. 1.9; это кривая называется также синусоида, полученная в результате перемещения графика
представлен на рис. 1.9; это кривая называется также синусоида, полученная в результате перемещения графика 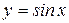 вдоль оси
вдоль оси 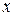 влево на
влево на  /2.
/2.
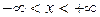 ;область значений:
;область значений: 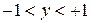 ;
;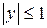 ), всюду непрерывные.
), всюду непрерывные.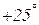 . Такие величины, как расстояние между точками и температура, называют скалярными величинами. Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 5 (км) к северо-востоку от пункта В, то недостаточно направить студента, указав расстояние в 5 (км) для того, чтобы он достиг пункт В. Необходимо задать направление движения. Комбинация модуля и направления физической величины называется векторной величиной, или просто вектором.
. Такие величины, как расстояние между точками и температура, называют скалярными величинами. Бывают обстоятельства, когда необходимо знать и модуль, и направление физической величины. Например, если пункт А находится в 5 (км) к северо-востоку от пункта В, то недостаточно направить студента, указав расстояние в 5 (км) для того, чтобы он достиг пункт В. Необходимо задать направление движения. Комбинация модуля и направления физической величины называется векторной величиной, или просто вектором.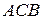 )вычисляется алгебраическим сложением (рис. 1.10, а):
)вычисляется алгебраическим сложением (рис. 1.10, а):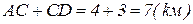
 а полное перемещениевычисляется расстояниеммежду пунктами А и В, котороеравно
а полное перемещениевычисляется расстояниеммежду пунктами А и В, котороеравно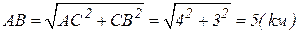 .
.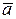 (
(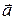 ) и изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины (рис. 1.10, б). Вектор характеризуется точкой приложения (точка А), модулем
) и изображается направленным отрезком, длина которого в некотором масштабе равна модулю представляемой вектором физической величины (рис. 1.10, б). Вектор характеризуется точкой приложения (точка А), модулем 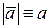 и линией действия – прямой, вдоль которой направлен вектор. Вектор, модуль которого
и линией действия – прямой, вдоль которой направлен вектор. Вектор, модуль которого 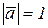 , называется единичным вектором. Если направление единичного вектора совпадает с направлением вектора, единичный вектор называется ортом. Орты, направленные по осям
, называется единичным вектором. Если направление единичного вектора совпадает с направлением вектора, единичный вектор называется ортом. Орты, направленные по осям 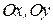 ,
, 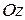 декартовой системы координат, обозначаются
декартовой системы координат, обозначаются 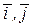 ,
, 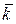 – единичные орты (рис. 1.11).
– единичные орты (рис. 1.11). Проекция вектора на ось. Изобразим вектор
Проекция вектора на ось. Изобразим вектор 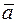 (рис. 11). Опустим перпендикуляры из начала А и конца В вектора на оси
(рис. 11). Опустим перпендикуляры из начала А и конца В вектора на оси 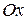 ,
, 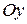 ,
, 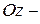 получим отрезки
получим отрезки 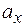 ,
, 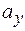 ,
, 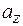 называемые проекциями вектора
называемые проекциями вектора 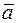 на оси
на оси 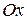 ,
, 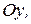
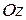 .
.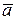 может бытьединственным образом разложен на сумму векторов, параллельных единичным ортам
может бытьединственным образом разложен на сумму векторов, параллельных единичным ортам 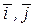 плоской системы:
плоской системы: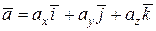 . (а)
. (а)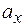 ,
, 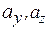 называются координатами вектора
называются координатами вектора 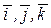 и обозначается это так
и обозначается это так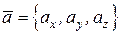 . (б)
. (б)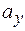 ,
, 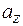 и модуль вычисляются по формулам:
и модуль вычисляются по формулам: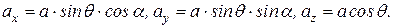 ,
, 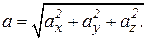

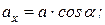
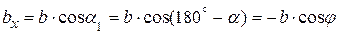 .
.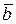 , приведенных к общему началу, есть третий вектор
, приведенных к общему началу, есть третий вектор 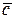 , длина которого равна длине параллелограмма, построенного на векторах
, длина которого равна длине параллелограмма, построенного на векторах 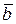 , а направлен вектор
, а направлен вектор 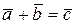 .
. Рис. 1.13
Рис. 1.13
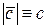 вычисляется по формуле
вычисляется по формуле
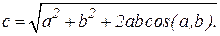 Силовой многоугольник. Суммируют несколько векторов построением векторного многоугольника. Слагаемые векторы путем параллельного переноса последовательно при-
Силовой многоугольник. Суммируют несколько векторов построением векторного многоугольника. Слагаемые векторы путем параллельного переноса последовательно при-
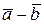 называется векторов
называется векторов 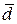 (диагональ BD) такой, что сумма векторов
(диагональ BD) такой, что сумма векторов 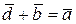
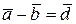 .
.
 г
г
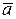 и
и 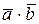 ) называется скаляр, определяемый равенством
) называется скаляр, определяемый равенством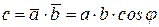 ,
,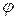 – угол между векторами
– угол между векторами 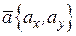 ,
, 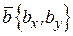 то скалярное произведение этих векторов вычисляется по формуле
то скалярное произведение этих векторов вычисляется по формуле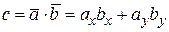 .
.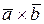 ) называется вектор
) называется вектор 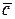 , длина которого равна
, длина которого равна 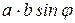 (т.е. площади параллелограмма, построенного на векторах, как на сторонах) и который направлен перпендикулярно плоскости расположения векторов
(т.е. площади параллелограмма, построенного на векторах, как на сторонах) и который направлен перпендикулярно плоскости расположения векторов 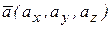 ,
, 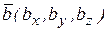 ,
, 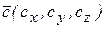 , то векторное произведение вычисляется по формуле
, то векторное произведение вычисляется по формуле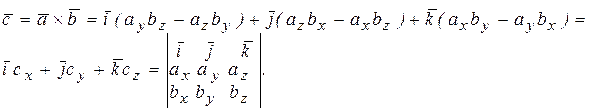
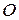 в евклидовом пространстве. Проведем через неподвижную точку
в евклидовом пространстве. Проведем через неподвижную точку 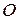 произвольно ось
произвольно ось 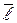 . Если каждому значению скалярного аргумента t поставить в соответствие вектор
. Если каждому значению скалярного аргумента t поставить в соответствие вектор 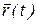 (расстояние между точкой
(расстояние между точкой 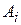 на траектории и полюсом О фиксируется
на траектории и полюсом О фиксируется 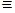 модулем
модулем 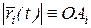 , направление прямой
, направление прямой 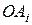 фиксируется углом
фиксируется углом 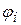 ) то функция
) то функция 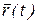 будет называться радиус–вектором скалярного аргумента (рис. 15, а). Если начало вектора
будет называться радиус–вектором скалярного аргумента (рис. 15, а). Если начало вектора  диус-вектора) находится в точке О, то конец радиус-вектора
диус-вектора) находится в точке О, то конец радиус-вектора 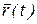 опишет пространственную кривую, которую называют годографом (записыватель пути) векторной функции (рис. 15, а). Если t означает время, то
опишет пространственную кривую, которую называют годографом (записыватель пути) векторной функции (рис. 15, а). Если t означает время, то 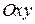 . Совместим с точкой
. Совместим с точкой 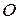 начало плоской декартовой системы, а ось
начало плоской декартовой системы, а ось 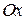 с осью
с осью 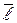 (рис. 1.15, б). В плоской декартовой системе координат радиус–вектор
(рис. 1.15, б). В плоской декартовой системе координат радиус–вектор 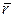 раскладывается по базисным векторам
раскладывается по базисным векторам 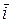 ,
, 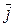 так (рис. 1.15, б)
так (рис. 1.15, б)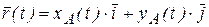 ,
,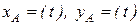 являются координатами точки А в прямоугольной системе координат.
являются координатами точки А в прямоугольной системе координат. Рис. 1.16
Рис. 1.16
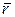 можно разложить по базисным векторам
можно разложить по базисным векторам 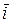 ,
, 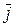 ,
, 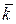 прямоугольной пространственной системы координат, то (рис.1.16)
прямоугольной пространственной системы координат, то (рис.1.16)
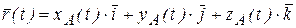 ,
причем компоненты
,
причем компоненты 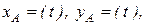
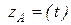 являются координатами точки А в прямоугольной системе координат.
являются координатами точки А в прямоугольной системе координат.


