Один из подходов численного решения дифференциальных уравнений это метод конечных разностей (метод сеток). Следуя этому подходу, область решения 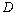 представляется в виде дискретного (обычно равномерного) набора (сетки) точек (узлов). Прямоугольная сетка в области
представляется в виде дискретного (обычно равномерного) набора (сетки) точек (узлов). Прямоугольная сетка в области 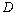 может быть задана как (рис. 6.1)
может быть задана как (рис. 6.1)
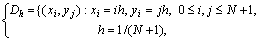
где величина 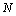 задает количество узлов по каждой из координат области
задает количество узлов по каждой из координат области 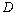 .
.
Обозначим оцениваемую при подобном дискретном представлении аппроксимацию функции 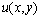 в точках
в точках 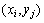 через
через 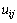 . Используя пятиточечный шаблон (рис. 6.1) для вычисления значений производных, уравнение Пуассона может быть представлено в конечно-разностной форме
. Используя пятиточечный шаблон (рис. 6.1) для вычисления значений производных, уравнение Пуассона может быть представлено в конечно-разностной форме
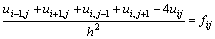 .
.
Данное уравнение может быть разрешено относительно 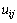
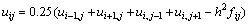 .
.
Разностное уравнение, которое записано записано в подобной форме, позволяет определять значение 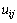 по известным значениям функции
по известным значениям функции 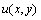 в соседних узлах используемого шаблона. Такой результат служит основой для построения различных итерационных схем решения задачи Дирихле, в которых в начале вычислений формируется некоторое приближение для значений
в соседних узлах используемого шаблона. Такой результат служит основой для построения различных итерационных схем решения задачи Дирихле, в которых в начале вычислений формируется некоторое приближение для значений 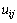 , а потом эти значения последовательно уточняются в соответствии с приведенным соотношением. Так, к примеру, метод Гаусса-Зейделя для проведения итераций уточнения использует правило
, а потом эти значения последовательно уточняются в соответствии с приведенным соотношением. Так, к примеру, метод Гаусса-Зейделя для проведения итераций уточнения использует правило
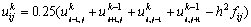 ,
,
по которому очередное k -ое приближение значения 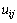 вычисляется по последнему k -ому приближению значений
вычисляется по последнему k -ому приближению значений 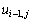 и
и 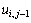 и предпоследнему (k-1)-ому приближению значений
и предпоследнему (k-1)-ому приближению значений 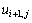 и
и 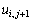 . Выполнение итераций обычно продолжается до тех пор, пока получаемые в результате итераций изменения значений
. Выполнение итераций обычно продолжается до тех пор, пока получаемые в результате итераций изменения значений 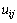 не станут меньше некоторой заданной величины (определяемой необходимой точностью вычислений). Сходимость описанной процедуры является предметом всестороннего математического анализа. Так же стоит учесть что последовательность решений, получаемых методом сеток, равномерно сходится к решению задачи Дирихле, а погрешность решения имеет порядок
не станут меньше некоторой заданной величины (определяемой необходимой точностью вычислений). Сходимость описанной процедуры является предметом всестороннего математического анализа. Так же стоит учесть что последовательность решений, получаемых методом сеток, равномерно сходится к решению задачи Дирихле, а погрешность решения имеет порядок 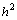 .
.
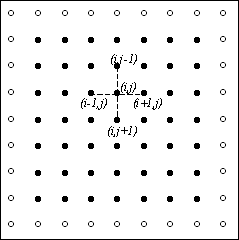
Рис. 6.1. Прямоугольная сетка в области D (нумерация узлов в строках слева направо, а в столбцах - сверху вниз, а темные точки представляют внутренние узлы сетки).
Метод Гаусса-Зейделя на псевдокоде, приближенном к алгоритмическому языку С++ представлен в виде:
// Алгоритм 6.1 do { dmax = 0; // максимальное изменение значений u for (i=1; i<N+1; i++) for (j=1; j<N+1; j++) { temp = u[i][j]; u[i][j] = 0.25*(u[i-1][j]+u[i+1][j]+ u[i][j-1]+u[i][j+1]–h*h*f[i][j]); dm = fabs(temp-u[i][j]); if (dmax < dm) dmax = dm; } } while (dmax > eps);
(напомним, что значения 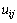 при индексах
при индексах 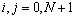 являются граничными, задаются при постановке задачи и не изменяются в ходе вычислений).
являются граничными, задаются при постановке задачи и не изменяются в ходе вычислений).

Рис. 6.2. Вид функции 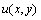 в примере для задачи Дирихле
в примере для задачи Дирихле
Для примера на рис. 6.2 приведен вид функции 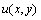 , полученной для задачи Дирихле при следующих условиях:
, полученной для задачи Дирихле при следующих условиях:
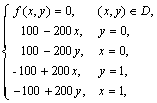
Общее количество итераций метода Гаусса-Зейделя составило 210 при точности решения 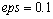 и
и 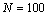 (в качестве начального приближения величин
(в качестве начального приближения величин 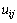 использовались значения, сгенерированные датчиком случайных чисел из диапазона [-100,100]).
использовались значения, сгенерированные датчиком случайных чисел из диапазона [-100,100]).





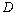 представляется в виде дискретного (обычно равномерного) набора (сетки) точек (узлов). Прямоугольная сетка в области
представляется в виде дискретного (обычно равномерного) набора (сетки) точек (узлов). Прямоугольная сетка в области 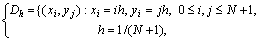
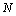 задает количество узлов по каждой из координат области
задает количество узлов по каждой из координат области 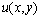 в точках
в точках 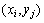 через
через 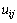 . Используя пятиточечный шаблон (рис. 6.1) для вычисления значений производных, уравнение Пуассона может быть представлено в конечно-разностной форме
. Используя пятиточечный шаблон (рис. 6.1) для вычисления значений производных, уравнение Пуассона может быть представлено в конечно-разностной форме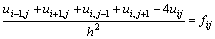 .
.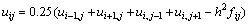 .
.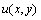 в соседних узлах используемого шаблона. Такой результат служит основой для построения различных итерационных схем решения задачи Дирихле, в которых в начале вычислений формируется некоторое приближение для значений
в соседних узлах используемого шаблона. Такой результат служит основой для построения различных итерационных схем решения задачи Дирихле, в которых в начале вычислений формируется некоторое приближение для значений 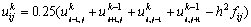 ,
,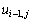 и
и 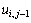 и предпоследнему (k-1)-ому приближению значений
и предпоследнему (k-1)-ому приближению значений 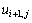 и
и 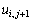 . Выполнение итераций обычно продолжается до тех пор, пока получаемые в результате итераций изменения значений
. Выполнение итераций обычно продолжается до тех пор, пока получаемые в результате итераций изменения значений 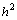 .
.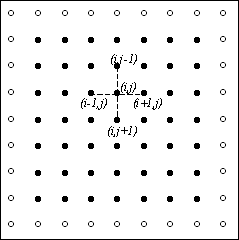
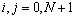 являются граничными, задаются при постановке задачи и не изменяются в ходе вычислений).
являются граничными, задаются при постановке задачи и не изменяются в ходе вычислений).
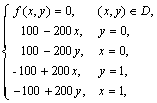
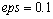 и
и 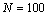 (в качестве начального приближения величин
(в качестве начального приближения величин 

