Подход, рассмотренный в п. 4, уменьшает эффект состязания потоков, но не гарантирует единственности решения при повторении вычислений. Для достижения однозначности необходимо использование дополнительных вычислительных схем.
Одним из широко применяемых на практике способ состоит в разделении места хранения результатов вычислений на предыдущей и текущей итерациях метода сеток. Схема такого подхода представлена в общем виде:
// Алгоритм 6.4 omp_lock_t dmax_lock; omp_init_lock(dmax_lock); do { dmax = 0; // максимальное изменение значений u
#pragma omp parallel for shared(u,n,dmax) private(i,temp,d,dm) for (i=1; i<N+1; i++) { dm = 0; for (j=1; j<N+1; j++) { temp = u[i][j];
un [i][j] = 0.25*(u[i-1][j]+u[i+1][j]+ u[i][j-1]+u[i][j+1]–h*h*f[i][j]); d = fabs(temp-
un [i][j]); if (dm < d) dm = d; } omp_set_lock(dmax_lock); if (dmax < dm) dmax = dm; omp_unset_lock(dmax_lock); } } // конец параллельной области
for (i=1; i<N+1; i++) // обновление данных
for (j=1; j<N+1; j++) u[i][j] = un[i][j]; } while (dmax > eps);
Как следует из приведенного алгоритма, результаты предыдущей итерации запоминаются в массиве u, новые вычисления значения запоминаются в дополнительном массиве un. Как результат, независимо от порядка выполнения вычислений для проведения расчетов всегда используются значения величин 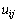 от предыдущей итерации метода. Такая схема реализация сеточных алгоритмов обычно именуется методом Гаусса-Якоби, гарантирующего однозначные результаты независимо от способа распараллеливания, но при этом требует использования большого дополнительного объема памяти и обладает меньшей (по сравнению с алгоритмом Гаусса-Зейделя) скоростью сходимости. Результаты приведены в табл. 6.2.
от предыдущей итерации метода. Такая схема реализация сеточных алгоритмов обычно именуется методом Гаусса-Якоби, гарантирующего однозначные результаты независимо от способа распараллеливания, но при этом требует использования большого дополнительного объема памяти и обладает меньшей (по сравнению с алгоритмом Гаусса-Зейделя) скоростью сходимости. Результаты приведены в табл. 6.2.
Таблица 6.2. Результаты вычислительных экспериментов
для алгоритма Гаусса-Якоби (p =4)
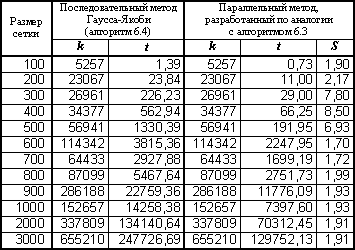
(k – количество итераций, t – время в сек., S – ускорение)
Другой возможный подход для устранения взаимозависимости параллельных потоков состоит в применении схемы чередования обработки четных и нечетных строк (red/black row alternation scheme), когда выполнение итерации метода сеток подразделяется на два последовательных этапа, на первом из которых обрабатываются строки только с четными номерами, а на втором этапе - строки с нечетными номерами (рис. 6.7). Эту схему можно обобщить на применение одновременно и к строкам, и к столбцам (шахматное разбиение) области расчетов.
Схема чередования строк не требует по сравнению с методом Якоби какой-либо дополнительной памяти и обеспечивает однозначность решения при многократных запусках программы. Но при этом оба рассмотренных подхода могут получать результаты, не совпадающие с решением задачи Дирихле, найденном при помощи последовательного алгоритма. Кроме этого, эти вычислительные схемы имеют меньшую область и худшую скорость сходимости, чем изначальный вариант метода Гаусса-Зейделя.
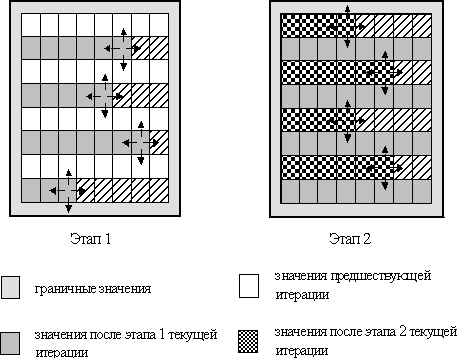
Рис. 6.7. Схема чередования обработки четных и нечетных строк





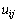 от предыдущей итерации метода. Такая схема реализация сеточных алгоритмов обычно именуется методом Гаусса-Якоби, гарантирующего однозначные результаты независимо от способа распараллеливания, но при этом требует использования большого дополнительного объема памяти и обладает меньшей (по сравнению с алгоритмом Гаусса-Зейделя) скоростью сходимости. Результаты приведены в табл. 6.2.
от предыдущей итерации метода. Такая схема реализация сеточных алгоритмов обычно именуется методом Гаусса-Якоби, гарантирующего однозначные результаты независимо от способа распараллеливания, но при этом требует использования большого дополнительного объема памяти и обладает меньшей (по сравнению с алгоритмом Гаусса-Зейделя) скоростью сходимости. Результаты приведены в табл. 6.2.




