В нормальной форме
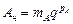 , ,
| (3.20)
|
где тА —мантисса числа А; рА —порядок числа А.
Как видно из ранее изложенного, такое представление чисел не однозначно; для определенности обычно вводят некоторые ограничения. Наиболее распространено и удобно для представления в ЭВМ ограничение вида
 , ,
| (3.21)
|
где q — основание системы счисления.
Нормализованная форма представления чисел - форма представления чисел, для которой справедливо условие (3.21).
Поскольку в этом случае абсолютное значение мантиссы лежит в пределах от q -1до 1 – q - n ,где п — количество разрядов для изображения мантиссы без знака, положение разрядов числа в его автоматном изображении не постоянно. Поэтому такую форму представления чисел называют также формой представления с плавающей запятой. Формат машинного изображения числа с плавающей запятой должен содержать знаковые части и поля для мантиссы и порядка (рис. 3.3, а). Выделяются специальные разряды для изображения знака числа (мантиссы) и знака порядка или характеристики (рис. 3.3, а, б). Кодирование знаков остается таким же, как было с фиксированной запятой.

Рис. 3.3. Представление чисел в форме с плавающей запятой
Рассмотрим пример записи чисел в форме с плавающей запятой. Пусть в разрядную сетку цифрового автомата (рис. 3.3) необходимо записать двоичные числа А 1=-10110,11112 и А 2=+0,0001100101112. Прежде всего эти числа необходимо записать в нормальной форме (рис. 3.3, в, г). Порядок чисел выбирают таким образом, чтобы для них выполнялось условие (3.21), т.е.  и
и  , он должен быть записан в двоичной системе счисления. Так как система счисления для заданного автомата остается постоянной, то нет необходимости указывать ее основание, достаточно лишь представить показатель степени.
, он должен быть записан в двоичной системе счисления. Так как система счисления для заданного автомата остается постоянной, то нет необходимости указывать ее основание, достаточно лишь представить показатель степени.
Поскольку для изображения порядка выделено пять цифровых разрядов и один разряд для знака, их машинные изображения и машинные изображения их мантисс соответственно
 ;
;  ;
;
 ;
; 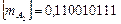 .
.
Лекция 6. Основные понятия алгебры логики
(7 неделя, 1 час)
Для формального описания цифрового автомата широко применяют аппарат алгебры логики, являющейся одним из важных разделов математической логики.
Основное понятие алгебры логики — высказывание. Высказывание — некоторое предложение, о котором можно утверждать, что оно истинно или ложно. Например, высказывание «Земля — это планета Солнечной системы» истинно, а о высказывании «на улице идет дождь» можно сказать, истинно оно или ложно, если указаны дополнительные сведения о погоде в данный момент.
Любое высказывание можно обозначить символом х и считать, что х = 1, если высказывание истинно, а х = 0 — если высказывание ложно.
Логическая (булева) переменная — такая величина х, которая может принимать только два значения: х = {0,1}.
Высказывание абсолютно истинно, если соответствующая ей логическая величина принимает значение х = 1при любых условиях. Пример абсолютно истинного высказывания — высказывание «Земля — планета Солнечной системы».
Высказывание абсолютно ложно, если соответствующая ей логическая величина принимает значение х = 0 при любых условиях.
Например, высказывание «Земля — спутник Марса» абсолютно ложно.
Логическая функция (функция алгебры логики) — функция f (x 1, x 2,..,хп), принимающая значение, равное нулю или единице на наборе логических переменных х1, х2,..., хп.
Логические функции от одной переменной представлены в таблице 2.1.
Таблица 7.1
| x
| f1 (x)
| f2 (x)
| f3 (x)
| f4 (x)
|
| 0
1
| 1
1
| 0
0
| 0
1
| 1
0
|
В соответствии с введенными определениями функция f 1 (x) является абсолютно истинной (константа единицы), а функция f 2 (x) — абсолютно ложной функцией (константа нуля).
Функция f 3 (x), повторяющая значения логической переменной, тождественная функция [ f 3 (x) 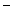 x ], а функция f 4 (x), принимающая значения, обратные значениям х, —логическое отрицание, или функция НЕ [ f 4 (x)=┐х =
x ], а функция f 4 (x), принимающая значения, обратные значениям х, —логическое отрицание, или функция НЕ [ f 4 (x)=┐х = 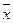 ].
].
Логические функции от двух переменных представлены в таблице 2.2.
Дизъюнкция (логическое сложение) — функция f 7 (x 1, x 2,), которая истинна тогда, когда истинны или х1, или х2, или обе переменные.
Дизъюнкцию часто называют также функцией ИЛИ и условно обозначают так: f 7 (x 1, x 2,)= x 1 + x 2 = x 1 Ú x 2
Таблица 7.2
От дизъюнкции следует отличать функцию f 6 (x 1, x 2), которая называется функцией сложения по модулю 2 (функцией исключительное ИЛИ) и является истинной, когда истинны или х1, или х2, в отдельности. Условное обозначение этой функции f 6 (x 1, x 2)= х1  х2.
х2.
Конъюнкция (логическое умножение} — функция f 1 (x 1, x 2), которая истинна только тогда, когда и xl, и х2 истинны. Конъюнкцию часто называют также функцией И; условно обозначают так: f 6 (x 1, x 2) = x 1 & х2 = x 1 Ù x 2.
Пример 7.1. Имеются два высказывания: «Завтра будет холодная погода», «Завтра пойдет снег».
Дизъюнкция этих высказываний — новое высказывание: «Завтра будет холодная погода или пойдет снег». Соединительный союз, который образовал новое предложение, — ИЛИ.
Конъюнкция образуется следующим образом: «Завтра будет холодная погода и пойдет снег». Это высказывание образовано с помощью союза И.
Штрих Шеффера — функция f 14 (x 1, x 2), которая ложна только тогда, когда х1 и х2 истинны. Условное обозначение функции Шеффера: f 14 (x 1, x 2)= x 1 / x 2. Немецкий математик Д. Шеффер на основе этой функции создал алгебру, названную алгеброй Шеффера.
Функция Пирса (Вебба) — функция f 8 (x 1, x 2), которая истинна только тогда, когда x 1, и х2 ложны. Условное обозначение этой функции: f 8 (x 1, x 2)= x 1  x 2 = x 1
x 2 = x 1  x 2.
x 2.
Математики Ч. Пирс и Д. Вебб, независимо друг от друга изучавшие свойства этой функции, создали алгебру, названную алгеброй Пирса (Вебба).
Импликация — функция f 13 (x 1, x 2), которая ложна тогда и только тогда, когда х1 истинно и х2 ложно. Условное обозначение: f 13 (x 1, x 2) = x 1  x 2.
x 2.
Все логические функции, приведенные в таблице 2.2, — элементарные функции.
Две функции равносильны друг другу, если принимают на всех возможных наборах переменных одни и те же значения:
f1 (x1, x2, …, xn)= f2 (x1, x2, …, xn).
Булевы переменные могут быть действительными или фиктивными. Переменная x 1 действительна, если значение функции f (x 1, …, xi,, …, xn) изменяется при изменении х i. Переменная х i фиктивна, если значение функции f 1 (x 1, x 2, …, xn) не изменяется при изменении х i.
Пример логической функции от трех переменных представлен в таблице 2.3.
Из таблицы видно, что переменные х1 и х2 — действительные, а переменная x 3 — фиктивная, так как f (xl, x 2,0)- f (x 1, x 2,1) для всех наборов х1, х2.
Таблица 7.3
| xl
| x2
| X3
| f (x1, x2, x3)
| xl
| x2
| x3
| f (x1, x2, x3)
|
| 0
| 0
| 0
| 0
| 1
| 0
| 0
| 1
|
| 0
| 0
| 1
| 0
| 1
| 0
| 1
| 1
|
| 0
| 1
| 0
| 1
| 1
| 1
| 0
| 0
|
| 0
| 1
| 1
| 1
| 1
| 1
| 1
| 0
|
Использование фиктивных функций дает возможность сокращать или расширять количество переменных для логических функций.
Так как число значений переменных х i ограничено, то можно определить количество функций N от любого числа переменных п: N =  .
.
Лекция 7. Основные понятия теории алгоритмов
(8 неделя, 1 час)
Понятие алгоритма - одно из фундаментальных понятий информатики. Алгоритмизация наряду с моделированием выступает в качестве общего метода информатики. К реализации определенных алгоритмов сводятся процессы управления в различных системах.
Алгоритмы являются объектом систематического исследования пограничной между математикой и информатикой научной дисциплины, примыкающей к математической логике - теории алгоритмов.
Термин «алгоритм» произошел от имени узбекского математика аль-Хорезми, который еще в IX в. сформулировал правила выполнения четырех арифметических действий. Появившееся несколько позже слово «алгорифм» связано с Евклидом, древнегреческим математиком, сформулировавшим правила нахождения наибольшего общего делителя двух чисел. В современной математике употребляют термин «алгоритм».
Существует несколько определений термина «алгоритм». Например, по определению акад. А.Н. Колмогорова, алгоритм или алгорифм – это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
В инженерной практике часто используется следующее определение: алгоритм – конечная совокупность точно сформулированных правил решения какой-то задачи.
Формальное определение алгоритма является фундаментальным теоретическим понятием. В практическом аспекте, информатика занимается разработкой алгоритмов решения различных задач и их реализацией для какого-либо исполнителя.
Часто решить одну и ту же проблему можно с помощью нескольких алгоритмов и нужно выбрать наилучший из них. На практике нам нужны не просто алгоритмы, а хорошие алгоритмы в широком смысле этого слова. Одним из критериев качества алгоритма является время, необходимое для его выполнения; данную характеристику можно оценить по тому, сколько раз выполняется каждый шаг. Другими критериями являются адаптируемость алгоритма к различным компьютерам, его простота, изящество и т. д. Решению этих вопросов посвящена область анализа алгоритмов.
Интуитивное понятие алгоритма обычно уточняется перечнем его свойств и введением понятия исполнителя алгоритма. Алгоритм всегда предполагает исполнителя, для которого и составляются предписания. Им может быть человек, компьютер и другие устройства. Описание алгоритма производится на языке исполнителя, чтобы он понимал предписываемые действия.
Машины Тьюринга и Поста были рассмотрены в лекции 4 как примеры цифровых автоматов. Как было сказано ранее, эти машины представляют собой универсальных исполнителей, являющихся полностью детерминированными, позволяющих «вводить» начальные данные, и после выполнения программ «читать» результат. Есть ли ограничения на вычисления, производимые на машинах Тьюринга и Поста. Ответ на этот вопрос был сформулирован самим Э. Постом в следующем виде: «Задача на составление программы, приводящей от исходного данного к результирующему числу, тогда и только тогда имеет решение, когда имеется какой-нибудь общий способ, позволяющий по произвольному и одному данному выписать результирующее число». Формулировка постулата Поста подводит к понятию алгоритма и подтверждает возможность решения этого алгоритма с помощью цифровых автоматов.
Нормальные алгоритмы Маркова. Для формализации понятия алгоритма российский математик А.А.Марков предложил использовать ассоциативные исчисления.
Рассмотрим некоторые понятия ассоциативного исчисления. Пусть имеется алфавит (конечный набор различных символов). Составляющие его символы будем называть буквами. Любая конечная последовательность букв алфавита (линейный их ряд) называется словом в этом алфавите.
Рассмотрим два слова N и М внекотором алфавите А. Если N является частью М, то говорят, что N входит в М.
Зададим в некотором алфавите конечную систему подстановок N - М, S - Т,..., где N, М, S, Т,... - слова в этом алфавите. Любую подстановку N - М можно применить к некоторому слову К следующим способом: если в К имеется одно или несколько вхождений слова N, то любое из них может быть заменено словом М, и, наоборот, если имеется вхождение М, то его можно заменить словом N.
Слова Р  и Р2 в некотором ассоциативном исчислении называются смежными, если одно из них может быть преобразовано в другое однократным применением допустимой подстановки.
и Р2 в некотором ассоциативном исчислении называются смежными, если одно из них может быть преобразовано в другое однократным применением допустимой подстановки.
Последовательность слов Р, Р1, Р2,,..., М называется дедуктивной цепочкой, ведущей от слова Р к слову М, если каждое из двух рядом стоящих слов этой цепочки - смежное.
Слова Р и М называют эквивалентными, если существует цепочка от Р к М и обратно.
Пример
| Алфавит
|
| Подстановки
|

| ac-ca;
|
| abac-abace
|
|
| ad-da;
|
| eca-ae
|
|
| bc-cb;
|
| eda-be
|
|
| bd-db;
|
| edb-be
|
Слова abcde и acbde - смежные (подстановка bc - cb). Слова abcde - cadbe эквивалентны.
Может быть рассмотрен специальный вид ассоциативного исчисления, в котором подстановки являются ориентированными: N  М (стрелка означает, что подстановку разрешается производить лишь слева направо). Для каждого ассоциативного исчисления существует задача: для любых двух слов определить, являются ли они эквивалентными или нет.
М (стрелка означает, что подстановку разрешается производить лишь слева направо). Для каждого ассоциативного исчисления существует задача: для любых двух слов определить, являются ли они эквивалентными или нет.
Любой процесс вывода формул, математические выкладки и преобразования также являются дедуктивными цепочками в некотором ассоциативном исчислении. Построение ассоциативных исчислений является универсальным методом детерминированной переработки информации и позволяет формализовать понятие алгоритма.
Введем понятие алгоритма на основе ассоциативного исчисления: алгоритмом в алфавите А называется понятное точное предписание, определяющее процесс над словами из А и допускающее любое слово в качестве исходного. Алгоритм в алфавите А задается в виде системы допустимых подстановок, дополненной точным предписанием о том, в каком порядке нужно применять допустимые подстановки и когда наступает остановка.
Пример
| Алфавит
|
| Система подстановок B
|
A= 
|
| cb-cc
|
|
|
| cca-ab
|
|
|
| ab-bca
|
Предписание о применении подстановок: в произвольном слове Р надо сделать возможные подстановки, заменив левую часть подстановок на правую; повторить процесс с вновь полученным словом.
Так, применяя систему подстановок В из рассмотренного примера к словам bаbаас и bcacabc, получаем:
babaac  bbcaaac
bbcaaac  остановка
остановка
bcacabc  bcacbcac
bcacbcac  bcacccac
bcacccac  bcacabc
bcacabc  бесконечный процесс (остановки нет), так как мы получили исходное слово.
бесконечный процесс (остановки нет), так как мы получили исходное слово.
Предложенный А.А.Марковым способ уточнения понятия алгоритма основан на понятии нормального алгоритма, который определяется следующим образом. Пусть задан алфавит А и система подстановок В. Для произвольного слова Р подстановки из В подбираются в том же порядке, в каком они следуют в В. Если подходящей подстановки нет, то процесс останавливается. В противном случае берется первая из подходящих подстановок и производится замена ее правой частью первого вхождения ее левой части в Р. Затем все действия повторяются для получившегося слова Р1. Если применяется последняя подстановка из системы В, процесс останавливается.
Такой набор предписаний вместе с алфавитом А и набором подстановок В определяют нормальный алгоритм. Процесс останавливается только в двух случаях: 1) когда подходящая подстановка не найдена; 2) когда применена последняя подстановка из их набора. Различные нормальные алгоритмы отличаются друг от друга алфавитами и системами подстановок.
Приведем пример нормального алгоритма, описывающего сложение натуральных чисел (представленных наборами единиц).
Пример
| Алфавит
|
| Система подстановок B
|
| A ={+,1}
|
| 1 +  + 1 + 1
|
|
|
| + 1  1 1
|
|
|
| 1  1 1
|
Слово P: 11 + 11 + 111.
Последовательная переработка слова Р с помощью нормального алгоритмаМаркова проходит через следующие этапы:
| P =11+11+111
| P 5=+1+111111
|
| P 1=1+111+111
| P 6=++1111111
|
| P 2=+1111+111
| P 7 =+1111111
|
| P 3=+111+1111
| P 8=1111111
|
| P 4=+11+11111
| P 9=1111111
|
Нормальный алгоритм Маркова можно рассматривать как универсальную форму задания любого алгоритма. Универсальность нормальных алгоритмов декларируется принципом нормализации: для любого алгоритма в произвольном конечном алфавите А можно построить эквивалентный ему нормальный алгоритм над алфавитом А.
Разъясним последнее утверждение. В некоторых случаях не удается построить нормальный алгоритм, эквивалентный данному в алфавите А, если использовать в подстановках алгоритма только буквы этого алфавита. Однако можно построить требуемый нормальный алгоритм, производя расширение алфавита А (добавляя к нему некоторое число новых букв). В этом случае говорят, что построенный алгоритм является алгоритмом над алфавитом А, хотя он будет применяться лишь к словам в исходном алфавите А.
Если алгоритм N задан в некотором расширении алфавита А, то говорят, что N есть нормальный алгоритм над алфавитом А.
Условимся называть тот или иной алгоритм нормализуемым, если можно построить эквивалентный ему нормальный алгоритм, и ненормализуемым в противном случае. Принцип нормализации теперь может быть высказан в видоизмененной форме: все алгоритмы нормализуемы.
Данный принцип не может быть строго доказан, поскольку понятие произвольного алгоритма не является строго определенным и основывается на том, что все известные в настоящее время алгоритмы являются нормализуемыми, а способы композиции алгоритмов, позволяющие строить новые алгоритмы из уже известных, не выводят за пределы класса нормализуемых алгоритмов. Ниже перечислены способы композиции нормальных алгоритмов.
I. Суперпозиция алгоритмов. При суперпозиции двух алгоритмов А и В выходное слово первого алгоритма рассматривается как входное слово второго алгоритма В, результат суперпозиции С может быть представлен в виде С(p) = В(А(p)).
II. Объединение алгоритмов. Объединением алгоритмов А и В в одном и том же алфавите называется алгоритм С в том же алфавите, преобразующий любое слово p, содержащееся в пересечении областей определения алгоритмов А и В, в записанные рядом слова А(p) и В(p).
III. Разветвление алгоритмов. Разветвление алгоритмов представляет собой композицию D трех алгоритмов А, В и С, причем область определения алгоритма D является пересечением областей определения всех трех алгоритмов А, В и С, а для любого слова p из этого пересечения D (p) = А(p), если С(p) = e, D (p) = B (p), если С(p) = e, где e - пустая строка.
IV. Итерация алгоритмов. Итерация (повторение) представляет собой такую композицию С двух алгоритмов А и В, что для любого входного слова р соответствующее слово С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.
Нормальные алгоритмы Маркова являются не только средством теоретических построений, но и основой специализированного языка программирования, применяемого как язык символьных преобразований при разработке систем искусственного интеллекта.
Существует строгое доказательство того, что по возможностям преобразования нормальные алгоритмы Маркова эквивалентны машинам Тьюринга.
Лекция 8. Анализ эффективности и сложности алгоритмов
(9 неделя, 1 час)
Анализируя алгоритм, можно получить представление о том, сколько времени займет решение данной задачи при помощи данного алгоритма. Для каждого рассматриваемого алгоритма мы оценим, насколько быстро решается задача на массиве входных данных длины N. Например, мы можем оценить, сколько сравнений потребует алгоритм сортировки при упорядочении списка из N величин по возрастанию, или подсчитать, сколько арифметических операций нужно для умножения двух матриц размером N х N.
Одну и ту же задачу можно решить с помощью различных алгоритмов. Анализ алгоритмов дает нам инструмент для выбора алгоритма. Рассмотрим, например, два алгоритма, в которых выбирается наибольшая из четырех величин:
| largest = a
if b > largest then
largest = b
end if
return a
if c > largest then
largest = c
end if
if d > largest then
largest = d
end if
return largest
| if a > b then
if a > с then
if a > d then
return a
else
return d
end if
else
if с > d then
return с
else
return d
end if
end if
else
if b > с then
if b > d then
return b
else
return d
end if
else
if с > d then
return с
else
return d
end if
end if
end if
|
При рассмотрении этих алгоритмов видно, что в каждом делается три сравнения. Первый алгоритм легче прочесть и понять, но с точки зрения выполнения на компьютере у них одинаковый уровень сложности. С точки зрения времени эти два алгоритма одинаковы, но первый требует больше памяти из-за временной переменной с именем largest. Это дополнительное место не играет роли, если сравниваются числа или символы, но при работе с другими типами данных оно может стать существенным. Многие современные языки программирования позволяют определить операторы сравнения для больших и сложных объектов или записей. В этих случаях размещение временной переменной может потребовать много места. При анализе эффективности алгоритмов нас будет в первую очередь интересовать вопрос времени, но в тех случаях, когда память играет существенную роль, мы будем обсуждать и ее.
Различные характеристики алгоритмов предназначены для сравнения эффективности двух разных алгоритма, решающих одну задачу. Поэтому мы никогда не будем сравнивать между собой алгоритм сортировки и алгоритм умножения матриц, а будем сравнивать друг с другом два разных алгоритма сортировки.
Результат анализа алгоритмов — не формула для точного количества секунд или компьютерных циклов, которые потребует конкретный алгоритм. Такая информация бесполезна, так как в этом случае нужно указывать также тип компьютера, используется ли он одним пользователем или несколькими, какой у него процессор и тактовая частота, полный или редуцированный набор команд на чипе процессора и насколько хорошо компилятор оптимизирует выполняемый код. Эти условия влияют на скорость работы программы, реализующей алгоритм. Учет этих условий означал бы, что при переносе программы на более быстрый компьютер алгоритм становится лучше, так как он работает быстрее. Но это не так, и поэтому наш анализ не учитывает особенностей компьютера.
В случае небольшой или простой программы количество выполненных операций как функцию от N можно посчитать точно. Однако в большинстве случаев в этом нет нужды. В § 1.4 показано, что разница между алгоритмом, который делает N + 5 операций, и тем, который делает N + 250 операций, становится незаметной, как только N становится очень большим. Тем не менее, мы начнем анализ алгоритмов с подсчета точного количества операций.
Еще одна причина, по которой мы не будем пытаться подсчитать все операции, выполняемые алгоритмом, состоит в том, что даже самая аккуратная его настройка может привести лишь к незначительному улучшению производительности. Рассмотрим, например, алгоритм подсчета числа вхождений различных символов в файл. Алгоритм для решения такой задачи мог бы выглядеть примерно так:
for all 256 символов do
обнулить счетчик
end for
while в файле еще остались символы do
ввести очередной символ
увеличить счетчик вхождений прочитанного символа на единицу
end while
Посмотрим на этот алгоритм. Он делает 256 проходов в цикле инициализации. Если во входном файле N символов, то втором цикле N проходов. Возникает вопрос «Что же считать?». В цикле for сначала инициализируется переменная цикла, затем в каждом проходе проверяется, что переменная не выходит за границы выполнения цикла, и переменная получает приращение. Это означает, что цикл инициализации делает 257 присваиваний (одно для переменной цикла и 256 для счетчика), 256 приращений переменной цикла, и 257 проверок того, что эта переменная находится в пределах границ цикла (одна дополнительная для остановки цикла). Во втором цикле нужно сделать N + 1раз проверку условия (+1 для последней проверки, когда файл пуст), и N приращений счетчика. Всего операций:
| Приращения
| N + 256
|
| Присваивания
| 257
|
| Проверки условий
| N + 258
|
Таким образом, при размере входного файла в 500 символов в алгоритме делается 1771 операция, из которых 770 приходится на инициализацию (43%). Теперь посмотрим, что происходит при увеличении величины N. Если файл содержит 50 000 символов, то алгоритм сделает 100 771 операцию, из которых только 770 связаны с инициализацией (что составляет менее 1% общего числа операций). Число операций инициализации не изменилось, но в процентном отношении при увеличении N их становится значительно меньше.
Теперь взглянем с другой стороны. Данные в компьютере организованы таким образом, что копирование больших блоков данных происходит с той же скоростью, что и присваивание. Мы могли бы сначала присвоить 16 счетчикам начальное значение, равное 0, а затем скопировать этот блок 15 раз, чтобы заполнить остальные счетчики. Это приведет к тому, что в циклах инициализации число проверок уменьшится до 33, присваиваний до 33 и приращений до 31. Количество операций инициализации уменьшается с 770 до 97, то есть на 87%. Если же мы сравним полученный выигрыш с числом операций по обработке файла в 50 000 символов, экономия составит менее 0.7% (вместо 100 771 операций мы затратим 100 098). Заметим, что экономия по времени могла бы быть даже больше, если бы мы сделали все эти инициализации без циклов, поскольку понадобилось бы только 31 простое присваивание, но этот дополнительный выигрыш дает лишь 0.07% экономии. Овчинка не стоит выделки.
Мы видим, что вес инициализации по отношению к времени выполнения алгоритма незначителен. В терминах анализа при увеличении объема входных данных стоимость инициализации становится пренебрежимо малой.
В самой ранней работе по анализу алгоритмов определена вычислимость алгоритма в машине Тьюринга. При анализе подсчитывается число переходов, необходимое для решения задачи. Анализ пространственных потребностей алгоритма подразумевает подсчет числа ячеек в ленте машины Тьюринга, необходимых для решения задачи. Такого рода анализ разумен, и он позволяет правильно определить относительную скорость двух алгоритмов, однако его практическое осуществление чрезвычайно трудно и занимает много времени. Сначала нужно строго описать процесс выполнения функций перехода в машине Тьюринга, выполняющей алгоритм, а затем подсчитать время выполнения — весьма утомительная процедура.
Другой, не менее осмысленный, способ анализа алгоритмов предполагает, что алгоритм записан на каком-либо языке высокого уровня вроде Pascal, С. C + +, Java или достаточно общем псевдокоде. Особенности псевдокода не играют существенной роли, если он реализует основные структуры управления, общие для всех алгоритмов. Такие структуры, как циклы вида for или while, механизм ветвления вида if, case или switch, присутствуют в любом языке программирования, и любой такой язык подойдет для наших целей. Всякий раз нам предстоит рассматривать один конкретный алгоритм — в нем редко будет задействовано больше одной функции или фрагмента программы, и поэтому мощность упомянутых выше языков вообще не играет никакой роли. Вот мы и будем пользоваться псевдокодом.
В некоторых языках программирования значения булевских выражений вычисляются сокращенным образом. Это означает, что член В в выражении A and В вычисляется только, если выражение А истинно, поскольку в противном случае результат оказывается ложным независимо от значения В. Аналогично, член В в выражении A or В не будет вычисляться, если выражение А истинно. Как мы увидим, не важно, считать ли число сравнений при проверке сложного условия равным 1 или 2. Поэтому, освоив основы этой главы, мы перестанем обращать внимание на сокращенные вычисления булевских выражений.
Лекция 9. Алгоритмы вида «разделяй и властвуй»
(10 неделя, 1 час)
Алгоритмы вида «разделяй и властвуй» обеспечивают компактный и мощный инструмент решения различных задач; в этом параграфе мы займемся не столько разработкой подобных алгоритмов, сколько их анализом. При подсчете числа сравнений в циклах нам достаточно подсчитать число сравнений в одной итерации цикла и умножить его на число итераций. Этот подсчет становится сложнее, если число итераций внутреннего цикла зависит от параметров внешнего.
Подсчет итераций алгоритмов вида «разделяй и властвуй» не очень прост: он зависит от рекурсивных вызовов, от подготовительных и завершающих действий. Обычно неочевидно, сколько раз выполняется та или иная функция при рекурсивных вызовах. В качестве примера рассмотрим следующий алгоритм вида «разделяй и властвуй».
| DivideAndConquer(data,N,solution)
|
| data
| набор входных данных
|
| N
| количество значений в наборе
|
| solution
| решение задачи
|
|
|
|
| if (N <= SizeLimit) then
|
| DirectSolution(data,N,solution)
|
| else
|
| DivideInput(data.N,smallerSets,smallerSizes,numberSmaller)
|
| for i=l to numberSmaller do
|
| DivideAndConquer(smallerSets[i],smallerSizes[i],smallSol[i])
|
| end for
|
| CombineSolutions(smallSol,numberSmaller,solution)
|
| end if
|
Этот алгоритм сначала проверяет, не мал ли размер задачи настолько, чтобы решение можно было найти с помощью простого нерекурсивного алгоритма (названного в тексте DirectSolution). и если это так, то происходит его вызов. Если задача слишком велика, то сначала вызывается процедура Dividelnput, которая разбивает входные данные на несколько меньших наборов (их число равно numberSmaller). Эти меньшие наборы могут быть все одного размера или их размеры могут существенно различаться. Каждый из элементов исходного входного набора попадает по крайней мере в один из меньших наборов, однако один и тот же элемент может попасть в несколько наборов. Затем происходит рекурсивный вызов алгоритма DivideAndConquer на каждом из меньших входных множеств, а функция CombineSolutions сводит полученные результаты воедино.
Факториал натурального числа несложно вычислить в цикле, однако в нижеследующем примере нам понадобится рекурсивный вариант этого вычисления. Факториал числа N равен N, умноженному на факториал числа N — 1. Поэтому годится следующий алгоритм:



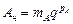 ,
,
 ,
,

 и
и  , он должен быть записан в двоичной системе счисления. Так как система счисления для заданного автомата остается постоянной, то нет необходимости указывать ее основание, достаточно лишь представить показатель степени.
, он должен быть записан в двоичной системе счисления. Так как система счисления для заданного автомата остается постоянной, то нет необходимости указывать ее основание, достаточно лишь представить показатель степени. ;
;  ;
; ;
; 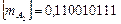 .
.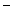 x ], а функция f 4 (x), принимающая значения, обратные значениям х, —логическое отрицание, или функция НЕ [ f 4 (x)=┐х =
x ], а функция f 4 (x), принимающая значения, обратные значениям х, —логическое отрицание, или функция НЕ [ f 4 (x)=┐х = 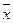 ].
]. (запрет x2)
(запрет x2)
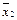 Ú x1 x2 = x1 (переменная x1)
Ú x1 x2 = x1 (переменная x1)
 x2 (запрет x1)
x2 (запрет x1)
 x2 (сложение по модулю 2)
x2 (сложение по модулю 2)
 x2 (функция Пирса)
x2 (функция Пирса)
 x2 (равнозначность)
x2 (равнозначность)
 Ú x1
Ú x1  =
=  x1 (импликация)
x1 (импликация)
 Ú
Ú  )
)
 x2 (импликация)
x2 (импликация)
 х2.
х2. x 2 = x 1
x 2 = x 1  x 2.
x 2. x 2.
x 2. .
. и Р2 в некотором ассоциативном исчислении называются смежными, если одно из них может быть преобразовано в другое однократным применением допустимой подстановки.
и Р2 в некотором ассоциативном исчислении называются смежными, если одно из них может быть преобразовано в другое однократным применением допустимой подстановки.
 М (стрелка означает, что подстановку разрешается производить лишь слева направо). Для каждого ассоциативного исчисления существует задача: для любых двух слов определить, являются ли они эквивалентными или нет.
М (стрелка означает, что подстановку разрешается производить лишь слева направо). Для каждого ассоциативного исчисления существует задача: для любых двух слов определить, являются ли они эквивалентными или нет.
 bcacccac
bcacccac  1
1



