Э квивалентность аксиоматик в учебниках геометрии Колмогорова А.Н. и Погорелова А.В.

КУРСОВАЯ РАБОТА

по дисциплине "Геометрия"

Э квивалентность аксиоматик в учебниках геометрии Колмогорова А.Н. и Погорелова А.В.

 

 

ОГТИ (филиал) ОГУ 050201.65. 5 0 12. 10 ОО

 

 

Руководитель работы ___________________ А. А. Уткин "_____"_________________ 2011 г. Исполнитель Студент гр. 08М ___________________ М. Л. Топузова "_____"_________________2012 г.

 

 

Орск 2012

 

Содержание

Ведение………………………………………………………………...........................3

§1. Общие вопросы аксиоматического метода……………………………………...5

§2. Задание математической структуры в школьных учебниках по геометрии Погорелова А.В. и Колмогорова А.М.

2.1 Математическая структура школьного учебника под редакцией

 Погорелова А.В.………………………………………………………………………6

2.2 математическая структура школьного учебника под редакцией

 Колмогорова А.Н……………………………………………………………………. 9

§3. Доказательство эквивалентности аксиоматик Погорелова А.В. и Колмогорова А.М……………………………………………………................................................13

Заключение……………………………………………………………………………

Список литературы…………………………………………………………………

 

 

Введение

Аксиоматический метод - фундаментальнейший метод организации и умножения научного знания в самых разных его областях - сформировался на протяжении более чем двухтысячелетней истории развития науки. А так же, аксиоматический метод – это способ построения научной теории, при котором в основу кладутся некоторые исходные положения, называемые аксиомами, а все остальные положения получаются как логическое следствие аксиом.

 Особую роль аксиоматический метод играет в математической науке. Можно сказать, что математическая наука достигает совершенства лишь тогда, когда ей удаётся пользоваться аксиоматическим методом, т.е., когда наука принимает характер аксиоматической теории. Более того, развитие науки в двадцатом столетии показало, что математика выделяется в системе наук именно тем, что она, по существу, единственная, использующая аксиоматический метод чрезвычайно широко, и что этот метод в значительной мере обуславливает поразительную эффективность математики в процессе познания окружающего мира и преобразующего воздействия на него.

Актуальность данной работы заключается в следующем:

1) Школьные учебники пишутся на основе аксиоматического метода;

2) В соответствии с законом об образовании, школа имеет право выбрать учебник;

3) Один учебник отличается друг от друга аксиоматиками, следовательно, и способом изложения геометрического материала;

4) Учитель математики должен хорошо предоставлять эквивалентность аксиоматик и должен уметь проводить доказательство эквивалентности аксиоматик.

Целью моей курсовой работы является провести анализ школьных учебников под редакцией Колмогорова А.М. и Погорелова А.В. и провести доказательство эквивалентности аксиоматик данных авторов.

В связи с данной целью я поставила перед собой задачи:

1. Выявить суть аксиоматического метода построения геометрии;

2. Описать структуру школьных учебников под редакцией Колмогорова А.М. и Погорелова А.В.;

3. Провести доказательство эквивалентности аксиоматик данных авторов.

 

Курсовая работа состоит из введения, трех параграфов, заключения и списка использованной литературы.

Во введении описана актуальность темы, сформулирована цель, дана структура курсовой работы.

В первом параграфе рассмотрены суть аксиоматического метода построения теории, требования аксиоматического метода, основные сведения из общих вопросов аксиоматики.

Во втором параграфе я описала структуру школьного учебника под редакцией Погорелова А.В. и школьного учебника под редакцией Колмогорова А.М.  Выявлено множества понятий, отношений и прописана система аксиом, на которой определены отношения.

В третьем параграфе проведены ряд доказательств эквивалентности аксиоматик учебников по геометрии  Погорелова А.В. и Колмогорова А.М.

В заключение подведен анализ и итог выполненной работы.

 

 

§1. Общие вопросы аксиоматического метода

Исторический процесс развития взглядов на существо математики как науки привел к формированию фундаментальной концепции аксиоматического метода и понятия аксиоматической теории. Суть их состоит в следующем. Выбирается ряд первоначальных понятий, которые не определяются и используются без объяснения их смысла. Вместе с тем, все другие понятия, которые будут использоваться, должны быть строго определены через первоначальные неопределённые понятия и через понятия, смысл которых был определён раньше. Высказывания, определяющее таким способом значение понятия, называется определением, а само понятие, смысл которого определён, носит название определяемого понятия. Евклид сделал попытку строго определить все первоначальные понятия геометрии: точки, прямой, плоскости и т.д. Но совершенно ясно, что эти понятия должны определяться через какие-то другие, те в свою очередь, должны опираться на следующие понятия, и так далее, так что процесс бесконечен. Таким образом, первоначальные понятия аксиоматической теории не определяются.

Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике. Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них

Основные понятия выделяются следующим образом. Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие. Эти понятия и называются основными. Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недосказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами. Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения.

Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём. В этом и заключается логическое строение геометрии. Аксиомы и основные понятия составляют основания планиметрии. Так как нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики. В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем представить основные понятия в виде объектов любой природы, которые обладают свойствами, указанными в аксиомах.

 

Задание математической структуры в школьных учебниках по геометрии Погорелова А.В.

Структура школьного учебника под редакцией Погорелова А.В. основывается на четырех неопределяемых понятиях, четырех отношениях и списком аксиом.

S={M₁, M₂, М₃, М₄ Δ₁‚ Δ₂‚ Δ₃‚ Δ₄, }, где: M1 – множество точек, M2 – множество прямых, М₃ - множество плоскостей, М₄– множество радиан, Δ1 – отношение принадлежности точки и прямой, Δ2 – отношение лежать между, Δ₃ - отношение расстояния, Δ₄ - отношение существования.

Система аксиом состоит из пяти групп аксиом: Σ={I,II,II,IV,V}, где:

I группа аксиом – аксиомы принадлежности точек и прямых на плоскости.

Аксиома. I  Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащей ей.

Через любые две точки можно провести прямую, и только одну.         a=AC, b=BC, т.к. B,C∊b, A,C∊a.

Следствие аксиомы . Две прямые либо не пересекаются, либо пересекаются только в одной точке.                                                                       

II группа – аксиомы расположения точек на прямой.

Аксиома. II.1 Из трех точек на прямой одна и только одна лежит между двумя другими.        μ(ΑCB), А∊a,B∊a,C∊a.

                                                                           А                   С          В

Аксиома. II.2 Прямая разбивает плоскость на две полуплоскости. ΑB⋔а, СD⋂а, АВ∊α, С∊α, D∊β                                                                                                   

Следствие аксиомы . Если прямая, не проходящая ни через одну из вершин треугольника, пересекается одну из его сторон, то она пересекает, и притом только одну, из двух других сторон.

Определение: треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, попарно соединяющих эти точки.

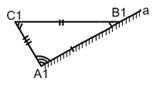
Аксиома. II.3 Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данный полупрямой.

                               

III группа – аксиомы измерения отрезков и углов.

Определение: Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя дальними ее точками.

 Аксиома III.1 Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

С∊ΑB, μ(ΑCB)=>|ΑB|=|ΑC|+|BC|          А                            С     В

Аксиома  позволяет ввести координату на прямой, т.е. сопоставить каждой точке прямой вещественное число так, что если и  - координаты точек А и В, то длина отрезка .

Определение: Угол называется фигура, которая состоит из точки – вершины угла - и двух различных полупрямых, исходящих из этой точки, - сторон угла.

Аксиома. III. 2 каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 градусов. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящем между его сторонами.

Если С проходит между сторонами угла (a^b), то (a^b) равен сумме углов (ас) и (ab).

IV – аксиомы откладывания отрезков и углов.

Определение: полупрямая или луч называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной точки, где А – начальная точка полупрямой а, C,Y,Z∊a, X,Y,Z – лежать по одну сторону от точки А, а⋂b=A.

Аксиома. IV.1 На любой полупрямой от ее начальной точки можно отложить отрезок заданной длинны и только один.

Аксиома. IV.2 От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 градусов, и только один.

V – аксиома параллельных прямых.

Определение: Две прямые называются параллельными, если они не пересекаются.

Аксиома.V Через точку, не лежащей на данной прямой, можно провести не более одной прямой, параллельной данной.

Α∊a, a – единственная прямая,a||b.

Следствия аксиомы V.

1. Свойство параллельности прямых транзитивно:  и , то .

2. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

 

Вывод: Анализ структуры школьного учебника под редакцией Погорелова показал, что структура состоит из четырех неопределяемых понятий, четырех отношений и списком аксиом, который в свою очередь разделен  на 5 групп. Следовательно, так как составлена конечная цепочка аксиом, поэтому на данном списке аксиом строиться математическая теория, задающая структуру. 

 

КУРСОВАЯ РАБОТА

по дисциплине "Геометрия"

Э квивалентность аксиоматик в учебниках геометрии Колмогорова А.Н. и Погорелова А.В.

 

 

ОГТИ (филиал) ОГУ 050201.65. 5 0 12. 10 ОО

 

 

Руководитель работы ___________________ А. А. Уткин "_____"_________________ 2011 г. Исполнитель Студент гр. 08М ___________________ М. Л. Топузова "_____"_________________2012 г.

 

 

Орск 2012

 

Содержание

Ведение………………………………………………………………...........................3

§1. Общие вопросы аксиоматического метода……………………………………...5

§2. Задание математической структуры в школьных учебниках по геометрии Погорелова А.В. и Колмогорова А.М.

2.1 Математическая структура школьного учебника под редакцией

 Погорелова А.В.………………………………………………………………………6

2.2 математическая структура школьного учебника под редакцией

 Колмогорова А.Н……………………………………………………………………. 9

§3. Доказательство эквивалентности аксиоматик Погорелова А.В. и Колмогорова А.М……………………………………………………................................................13

Заключение……………………………………………………………………………

Список литературы…………………………………………………………………

 

 

Введение

Аксиоматический метод - фундаментальнейший метод организации и умножения научного знания в самых разных его областях - сформировался на протяжении более чем двухтысячелетней истории развития науки. А так же, аксиоматический метод – это способ построения научной теории, при котором в основу кладутся некоторые исходные положения, называемые аксиомами, а все остальные положения получаются как логическое следствие аксиом.

 Особую роль аксиоматический метод играет в математической науке. Можно сказать, что математическая наука достигает совершенства лишь тогда, когда ей удаётся пользоваться аксиоматическим методом, т.е., когда наука принимает характер аксиоматической теории. Более того, развитие науки в двадцатом столетии показало, что математика выделяется в системе наук именно тем, что она, по существу, единственная, использующая аксиоматический метод чрезвычайно широко, и что этот метод в значительной мере обуславливает поразительную эффективность математики в процессе познания окружающего мира и преобразующего воздействия на него.

Актуальность данной работы заключается в следующем:

1) Школьные учебники пишутся на основе аксиоматического метода;

2) В соответствии с законом об образовании, школа имеет право выбрать учебник;

3) Один учебник отличается друг от друга аксиоматиками, следовательно, и способом изложения геометрического материала;

4) Учитель математики должен хорошо предоставлять эквивалентность аксиоматик и должен уметь проводить доказательство эквивалентности аксиоматик.

Целью моей курсовой работы является провести анализ школьных учебников под редакцией Колмогорова А.М. и Погорелова А.В. и провести доказательство эквивалентности аксиоматик данных авторов.

В связи с данной целью я поставила перед собой задачи:

1. Выявить суть аксиоматического метода построения геометрии;

2. Описать структуру школьных учебников под редакцией Колмогорова А.М. и Погорелова А.В.;

3. Провести доказательство эквивалентности аксиоматик данных авторов.

 

Курсовая работа состоит из введения, трех параграфов, заключения и списка использованной литературы.

Во введении описана актуальность темы, сформулирована цель, дана структура курсовой работы.

В первом параграфе рассмотрены суть аксиоматического метода построения теории, требования аксиоматического метода, основные сведения из общих вопросов аксиоматики.

Во втором параграфе я описала структуру школьного учебника под редакцией Погорелова А.В. и школьного учебника под редакцией Колмогорова А.М.  Выявлено множества понятий, отношений и прописана система аксиом, на которой определены отношения.

В третьем параграфе проведены ряд доказательств эквивалентности аксиоматик учебников по геометрии  Погорелова А.В. и Колмогорова А.М.

В заключение подведен анализ и итог выполненной работы.

 

 

§1. Общие вопросы аксиоматического метода

Исторический процесс развития взглядов на существо математики как науки привел к формированию фундаментальной концепции аксиоматического метода и понятия аксиоматической теории. Суть их состоит в следующем. Выбирается ряд первоначальных понятий, которые не определяются и используются без объяснения их смысла. Вместе с тем, все другие понятия, которые будут использоваться, должны быть строго определены через первоначальные неопределённые понятия и через понятия, смысл которых был определён раньше. Высказывания, определяющее таким способом значение понятия, называется определением, а само понятие, смысл которого определён, носит название определяемого понятия. Евклид сделал попытку строго определить все первоначальные понятия геометрии: точки, прямой, плоскости и т.д. Но совершенно ясно, что эти понятия должны определяться через какие-то другие, те в свою очередь, должны опираться на следующие понятия, и так далее, так что процесс бесконечен. Таким образом, первоначальные понятия аксиоматической теории не определяются.

Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех теоретических науках, прежде всего в математике. Аксиоматический метод построения научной теории заключается в следующем: выделяются основные понятия, формулируются аксиомы теории, а все остальные утверждения выводятся логическим путём, опираясь на них

Основные понятия выделяются следующим образом. Известно, что одно понятие должно разъясняться с помощью других, которые, в свою очередь, тоже определяются с помощью каких-то известных понятий. Таким образом, мы приходим к элементарным понятиям, которые нельзя определить через другие. Эти понятия и называются основными. Когда мы доказываем утверждение, теорему, то опираемся на предпосылки, которые считаются уже доказанными. Но эти предпосылки тоже доказывались, их нужно было обосновать. В конце концов, мы приходим к недосказываемым утверждениям и принимаем их без доказательства. Эти утверждения называются аксиомами. Набор аксиом должен быть таким, чтобы, опираясь на него, можно было доказать дальнейшие утверждения.

Выделив основные понятия и сформулировав аксиомы, далее мы выводим теоремы и другие понятия логическим путём. В этом и заключается логическое строение геометрии. Аксиомы и основные понятия составляют основания планиметрии. Так как нельзя дать единое определение основных понятий для всех геометрий, то основные понятия геометрии следует определить как объекты любой природы, удовлетворяющие аксиомам этой геометрии. Таким образом, при аксиоматическом построении геометрической системы мы исходим из некоторой системы аксиом, или аксиоматики. В этих аксиомах описываются свойства основных понятий геометрической системы, и мы можем представить основные понятия в виде объектов любой природы, которые обладают свойствами, указанными в аксиомах.

 

Задание математической структуры в школьных учебниках по геометрии Погорелова А.В.

Структура школьного учебника под редакцией Погорелова А.В. основывается на четырех неопределяемых понятиях, четырех отношениях и списком аксиом.

S={M₁, M₂, М₃, М₄ Δ₁‚ Δ₂‚ Δ₃‚ Δ₄, }, где: M1 – множество точек, M2 – множество прямых, М₃ - множество плоскостей, М₄– множество радиан, Δ1 – отношение принадлежности точки и прямой, Δ2 – отношение лежать между, Δ₃ - отношение расстояния, Δ₄ - отношение существования.

Система аксиом состоит из пяти групп аксиом: Σ={I,II,II,IV,V}, где:

I группа аксиом – аксиомы принадлежности точек и прямых на плоскости.

Аксиома. I  Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащей ей.

Через любые две точки можно провести прямую, и только одну.         a=AC, b=BC, т.к. B,C∊b, A,C∊a.

Следствие аксиомы . Две прямые либо не пересекаются, либо пересекаются только в одной точке.                                                                       

II группа – аксиомы расположения точек на прямой.

Аксиома. II.1 Из трех точек на прямой одна и только одна лежит между двумя другими.        μ(ΑCB), А∊a,B∊a,C∊a.

                                                                           А                   С          В

Аксиома. II.2 Прямая разбивает плоскость на две полуплоскости. ΑB⋔а, СD⋂а, АВ∊α, С∊α, D∊β                                                                                                   

Следствие аксиомы . Если прямая, не проходящая ни через одну из вершин треугольника, пересекается одну из его сторон, то она пересекает, и притом только одну, из двух других сторон.

Определение: треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, попарно соединяющих эти точки.

Аксиома. II.3 Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данный полупрямой.

                               

III группа – аксиомы измерения отрезков и углов.

Определение: Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя дальними ее точками.

 Аксиома III.1 Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

С∊ΑB, μ(ΑCB)=>|ΑB|=|ΑC|+|BC|          А                            С     В

Аксиома  позволяет ввести координату на прямой, т.е. сопоставить каждой точке прямой вещественное число так, что если и  - координаты точек А и В, то длина отрезка .

Определение: Угол называется фигура, которая состоит из точки – вершины угла - и двух различных полупрямых, исходящих из этой точки, - сторон угла.

Аксиома. III. 2 каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 градусов. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящем между его сторонами.

Если С проходит между сторонами угла (a^b), то (a^b) равен сумме углов (ас) и (ab).

IV – аксиомы откладывания отрезков и углов.

Определение: полупрямая или луч называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной точки, где А – начальная точка полупрямой а, C,Y,Z∊a, X,Y,Z – лежать по одну сторону от точки А, а⋂b=A.

Аксиома. IV.1 На любой полупрямой от ее начальной точки можно отложить отрезок заданной длинны и только один.

Аксиома. IV.2 От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 градусов, и только один.

V – аксиома параллельных прямых.

Определение: Две прямые называются параллельными, если они не пересекаются.

Аксиома.V Через точку, не лежащей на данной прямой, можно провести не более одной прямой, параллельной данной.

Α∊a, a – единственная прямая,a||b.

Следствия аксиомы V.

1. Свойство параллельности прямых транзитивно:  и , то .

2. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

 

Вывод: Анализ структуры школьного учебника под редакцией Погорелова показал, что структура состоит из четырех неопределяемых понятий, четырех отношений и списком аксиом, который в свою очередь разделен  на 5 групп. Следовательно, так как составлена конечная цепочка аксиом, поэтому на данном списке аксиом строиться математическая теория, задающая структуру.