При сопоставлении различных способов аппроксимации диаграмм деформирования пластичных конструкционных материалов, на которых отсутствует площадка текучести, с экспериментальными данными было установлено, что определенными преимуществами (простота, адекватность) обладает функция вида
 (1)
(1)
(аппроксимация диаграммы деформирования по Рамбергу–Осгуду); здесь
p =ln(1+ p) - логарифмическая пластическая деформация;
 =exp(p) - действительное напряжение;
=exp(p) - действительное напряжение;
K, m - постоянные материала, зависящие от температуры и скорости деформирования.
Поскольку диаграммы истинных и условных напряжений в области предела текучести практически совпадают:  @ s, р @ ep, при известном значении показателя упрочнения m коэффициент прочности K может быть найден исходя из равенства
@ s, р @ ep, при известном значении показателя упрочнения m коэффициент прочности K может быть найден исходя из равенства
 . (2)
. (2)
С другой стороны, известно, что диаграмма условных напряжений пластичного материала имеет отчетливо выраженный максимум, то есть, при 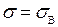 в точке, соответствующей временному сопротивлению, производная
в точке, соответствующей временному сопротивлению, производная 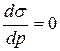 . Учитывая связь истинного и условного напряжений (см. выше), последнее можно представить в функции логарифмической неупругой деформации:
. Учитывая связь истинного и условного напряжений (см. выше), последнее можно представить в функции логарифмической неупругой деформации:
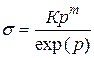 .
.
Дифференцируя это выражение по параметру р и приравнивая получившийся результат нулю
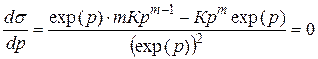 ,
,
получаем
 .
.
Соответственно определим коэффициент прочности:
 . (3)
. (3)
И, наконец, величина K может быть найдена путем осреднения этих двух результатов:
 .
.
Обычно все три значения K не слишком отличаются друг от друга, тем не менее, если предполагается работать в области сравнительно небольших пластических деформаций, целесообразно использовать формулу (2), высоких, в частности, в области разрушения – (3). Если же вся кривая деформирования должна быть аппроксимирована с одинаковой точностью, следует воспользоваться последним выражением.
Опыт расчетов показывает, что для конструкционных сталей и сплавов величина показателя упрочнения m изменяется в пределах  . Оказалось, что внутри данного диапазона зависимость
. Оказалось, что внутри данного диапазона зависимость 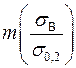 допустимо аппроксимировать линейной функцией. В результате обработки представительного набора опытных данных и определения методом наименьших квадратичных отклонений констант названной зависимости были получены удобные для практических расчетов выражения:
допустимо аппроксимировать линейной функцией. В результате обработки представительного набора опытных данных и определения методом наименьших квадратичных отклонений констант названной зависимости были получены удобные для практических расчетов выражения:

| (4)
|
Погрешность определения показателя упрочнения по этим формулам не превышает 3%.
Как следует из вышеизложенного, действительные значения  временного сопротивления
временного сопротивления  и напряжения в момент разрушения
и напряжения в момент разрушения  (истинное сопротивление разрыву) определяются следующими зависимостями:
(истинное сопротивление разрыву) определяются следующими зависимостями:
 ;
;
 (5)
(5)
(по-прежнему  – ресурс пластичности материала;
– ресурс пластичности материала;  – относительное сужение при разрыве).
– относительное сужение при разрыве).
Для пластичных материалов (у которых, как известно,  ) ресурс пластичности нетрудно найти, если известно истинное сопротивление разрыву:
) ресурс пластичности нетрудно найти, если известно истинное сопротивление разрыву:
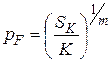 .
.
Предел пропорциональности определяют как напряжение, при котором касательный модуль  становится в полтора раза меньше модуля упругости Е (рис. 9):
становится в полтора раза меньше модуля упругости Е (рис. 9):
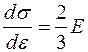 .
.

| Дифференцирование уравнения (1) с учетом допущения  =s, e = e и использованием последнего условия приводит к выражениям для расчета предела пропорциональности: =s, e = e и использованием последнего условия приводит к выражениям для расчета предела пропорциональности:
 (6)
или
(6)
или  . .
|
| Рис. 9. К определению предела пропорциональности
|
Диаграмма деформирования  малопластичных материалов имеет максимум в точке
малопластичных материалов имеет максимум в точке  =s В, иными словами, их разрушение происходит при достижении предела прочности. В этом случае механические характеристики прочности и пластичности определяют (в зависимости от известных и подлежащих определению величин) следующим образом:
=s В, иными словами, их разрушение происходит при достижении предела прочности. В этом случае механические характеристики прочности и пластичности определяют (в зависимости от известных и подлежащих определению величин) следующим образом:
 .
.
Сопротивление материала динамическим (ударным) нагрузкам вполне объективно характеризуется отношением
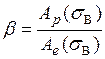 ,
,
где  – работа напряжения при пластическом деформировании элемента объема до величины, отвечающей временному сопротивлению s B (определяет соответствующую диссипацию энергии);
– работа напряжения при пластическом деформировании элемента объема до величины, отвечающей временному сопротивлению s B (определяет соответствующую диссипацию энергии);  – работа напряжения на соответствующей упругой деформации.
– работа напряжения на соответствующей упругой деформации.
Понятно, что чем больше величина  , тем выше «энергоемкость» и демпфирующая способность материала и, значит, тем лучше он противостоит динамическому воздействию. При аппроксимации кривой деформирования степенной зависимостью (1) величина
, тем выше «энергоемкость» и демпфирующая способность материала и, значит, тем лучше он противостоит динамическому воздействию. При аппроксимации кривой деформирования степенной зависимостью (1) величина  может быть подсчитана по формуле
может быть подсчитана по формуле
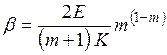 .
.





 (1)
(1) =exp(p) - действительное напряжение;
=exp(p) - действительное напряжение; @ s, р @ ep, при известном значении показателя упрочнения m коэффициент прочности K может быть найден исходя из равенства
@ s, р @ ep, при известном значении показателя упрочнения m коэффициент прочности K может быть найден исходя из равенства . (2)
. (2)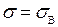 в точке, соответствующей временному сопротивлению, производная
в точке, соответствующей временному сопротивлению, производная 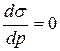 . Учитывая связь истинного и условного напряжений (см. выше), последнее можно представить в функции логарифмической неупругой деформации:
. Учитывая связь истинного и условного напряжений (см. выше), последнее можно представить в функции логарифмической неупругой деформации: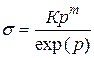 .
.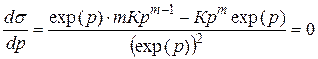 ,
, .
. . (3)
. (3) .
. . Оказалось, что внутри данного диапазона зависимость
. Оказалось, что внутри данного диапазона зависимость 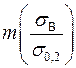 допустимо аппроксимировать линейной функцией. В результате обработки представительного набора опытных данных и определения методом наименьших квадратичных отклонений констант названной зависимости были получены удобные для практических расчетов выражения:
допустимо аппроксимировать линейной функцией. В результате обработки представительного набора опытных данных и определения методом наименьших квадратичных отклонений констант названной зависимости были получены удобные для практических расчетов выражения:
 временного сопротивления
временного сопротивления  и напряжения в момент разрушения
и напряжения в момент разрушения  (истинное сопротивление разрыву) определяются следующими зависимостями:
(истинное сопротивление разрыву) определяются следующими зависимостями: ;
; (5)
(5) – ресурс пластичности материала;
– ресурс пластичности материала;  – относительное сужение при разрыве).
– относительное сужение при разрыве). ) ресурс пластичности нетрудно найти, если известно истинное сопротивление разрыву:
) ресурс пластичности нетрудно найти, если известно истинное сопротивление разрыву: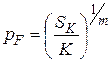 .
. становится в полтора раза меньше модуля упругости Е (рис. 9):
становится в полтора раза меньше модуля упругости Е (рис. 9):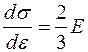 .
.
 =s, e = e и использованием последнего условия приводит к выражениям для расчета предела пропорциональности:
=s, e = e и использованием последнего условия приводит к выражениям для расчета предела пропорциональности:
 (6)
или
(6)
или  .
.
 малопластичных материалов имеет максимум в точке
малопластичных материалов имеет максимум в точке  =s В, иными словами, их разрушение происходит при достижении предела прочности. В этом случае механические характеристики прочности и пластичности определяют (в зависимости от известных и подлежащих определению величин) следующим образом:
=s В, иными словами, их разрушение происходит при достижении предела прочности. В этом случае механические характеристики прочности и пластичности определяют (в зависимости от известных и подлежащих определению величин) следующим образом: .
.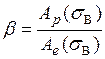 ,
, – работа напряжения при пластическом деформировании элемента объема до величины, отвечающей временному сопротивлению s B (определяет соответствующую диссипацию энергии);
– работа напряжения при пластическом деформировании элемента объема до величины, отвечающей временному сопротивлению s B (определяет соответствующую диссипацию энергии);  – работа напряжения на соответствующей упругой деформации.
– работа напряжения на соответствующей упругой деформации. , тем выше «энергоемкость» и демпфирующая способность материала и, значит, тем лучше он противостоит динамическому воздействию. При аппроксимации кривой деформирования степенной зависимостью (1) величина
, тем выше «энергоемкость» и демпфирующая способность материала и, значит, тем лучше он противостоит динамическому воздействию. При аппроксимации кривой деформирования степенной зависимостью (1) величина 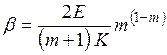 .
.


