Определения
Функция f(х), определенная на множестве S, достигает своего глобального минимума в точке x **Î S в том и только том случае, если
f(x**) £ f(x) для всех xÎ S.
Функция f(х), определенная на множестве S, имеет локальный, минимум (относительный минимум) в точке x*Î S в том и только том случае, если
f(x*) £ f(x), для всех х, удаленных от х * на расстояние, меньшее e,
т. е., если существует e > 0, такое, что для всех х, удовлетворяющих условию | х - х*|<e, выполняется неравенство f(x*)£ f(x).
Замечания
1. Аналогичные определения глобального максимума и локального максимума можно получить путем замены знака неравенства на противоположный.
2. Если функция обладает свойством унимодальности, то локальный минимум автоматически является глобальным минимумом.
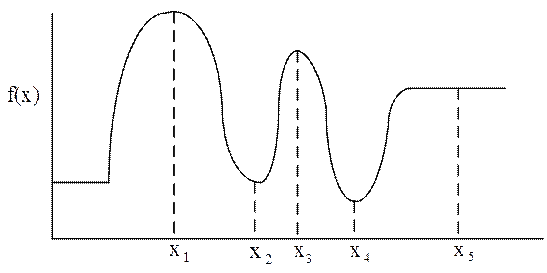
Рис. 6.48 Локальные и глобальные оптимумы
3. Если функция не является унимодальной, то возможно наличие нескольких локальных оптимумов; при этом глобальный минимум можно определить путем нахождения всех локальных оптимумов и выбора наименьшего из них.
Методы включения интервалов неопределенности
В разд. 4.2 рассматривался вопрос анализа «в статике», который заключается в том, чтобы определить, является ли данное решение оптимальным. Для этого были построены необходимые и достаточные условия оптимальности решения. Далее мы переходим к изучению вопроса анализа «в динамике», связанного с нахождением оптимального решения. С этой целью ниже рассматривается ряд одномерных методов поиска, ориентированных на нахождение точки оптимума внутри заданного интервала. Методы поиска, которые позволяют определить оптимум функции одной переменной путем последовательного исключения подынтервалов и, следовательно, путем уменьшения интервала поиска, носят название методов исключения интервалов.
В разд. 4.2. было дано определение унимодальной функции. Унимодальность функций является исключительно важным свойством. Фактически все одномерные методы поиска, используемые на практике, основаны на предположении, что исследуемая функция в допустимой области по крайней мере обладает свойством унимодальности. Полезность этого свойства определяется тем фактом, что для унимодальной функции f(x) сравнение значений f(x) в двух различных точках интервала поиска позволяет определить, в каком из заданных двумя указанными точками подынтервалов точка оптимума отсутствует.
Теорема
Пусть функция f унимодальна на замкнутом интервале а£ х £ в, а ее минимум достигается в точке х *. Рассмотрим точки х1 и х2 расположенные в интервале таким образом, что а < х1 < х2 < b. Сравнивая значения функции в точках х1 и х2 можно сделать еле дующие выводы.
1. Если f(х1)>f(х2), то точка минимума f(x) не лежит в интервале (a, х1), т. е. х* Î(х2, b) (рис. 6.49 а).
2. Если f(х1)<f(х2), то точка минимума не лежит в интервала (х2, b), т. е. х*Î (а,х2) (см. рис. 6.49 б).
Доказательство
Рассмотрим случай, когда f(х1)>f(х2). Пусть утверждение теоремы неверно, т. е. а£ х*£ х1. Поскольку х * – точка минимума, то по определению f(x*)£ f(x) для всех хÎ (а, b). Получаем двойное неравенство
f(x*)£ f(х1)>f(x2) при х*< х1 < x2.
Это неравенство не может выполняться, так как унимодальная функция f(х) должна быть монотонной по обе стороны от точки x *. Таким образом, получено противоречие, доказывающее утверждение теоремы. Аналогичные рассуждения справедливы также в случае, когда f(х1)<f (х2).
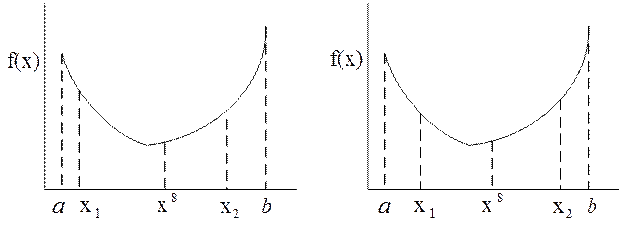
а) б)
Рис. 6.49 Графические иллюстрации к теореме
Примечание. Если f(х1)=f(х2), то можно исключить оба крайних интервала (a, х1) и (х2, b); при этом точка минимума должна располагаться в интервале (х1, х2).
Согласно теореме, которую иногда называют правилом исключения интервалов, можно реализовать процедуру поиска, позволяющую найти точку оптимума путем последовательного исключения частей исходного ограниченного интервала. Поиск завершается, когда оставшийся подынтервал уменьшается до достаточно малых размеров. Заметим, что правило, исключения интервалов устраняет необходимость полного перебора всех допустимых точек. Несомненным достоинством поисковых методов такого рода является то, что они основаны лишь на вычислении значений функций. При этом нe требуется, чтобы исследуемые функции были дифференцируемы; более того, допустимы случаи, когда функцию нельзя даже записать в аналитическом виде. Единственным требованием является возможность определения значений функции f(x) в заданных точках х с помощью прямых расчетов или имитационных, экспериментов. Вообще в процессе применения рассматриваемых методов поиска можно выделить два этапа:
этап установления границ интервала, на котором реализуется процедура поиска границ достаточно широкого интервала, содержащего точку оптимума;
этап уменьшения интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины.
Этап установления границ интервала. На этом этапе сначала выбирается исходная точка, а затем на основе правила исключения строится относительно широкий интервал, содержащий точку оптимума. Обычно поиск граничных точек такого интервала проводится с помощью эвристические методов поиска, хотя в ряде случаев можно также использовать методы экстраполяции. В соответствии с одним из эвристических методов, который был предложен Свенном (k +1)-я пробная точка определяется по рекуррентной формуле
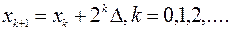
где х0 – произвольно выбранная начальная точка, D – подбираемая некоторым способом величина шага. Знак D определяется путем сравнения значений f(х0), f(х0+ |D|) и f(х0 - |D|). Если f(х0 - |D|)³ f(х0)³ f(х0+ |D|),
то, согласно предположению об унимодальности, точка минимума должна располагаться правее точки х0 и величина D выбирается положительной. Если изменить знаки неравенств на противоположные, то D следует выбирать отрицательной. Если же
f(х0 - |D|) ³ f(х0) £ f(х0+ |D|)
то точка минимума лежит между х0 - |D| и х0+ |D| и поиск граничных точек завершен. Случай, когда
f(х0 - |D|) £ f(х0) ³ f(х0+ |D|)
противоречит предположению об унимодальности. Выполнение этого условия свидетельствует о том, что функция не является унимодальной.
Пример
Рассмотрим задачу минимизации функции f(x)=( 100- х)2 при заданной начальной точке х0 =30 и величине шага |D|= 5.
Знак D определяется на основе сравнения значений
f(х0) = f (30) = 4900
f(х0+ |D|) = f (35) = 4225
f(х0 - |D|) = f (25) = 5625
то величина D должна быть положительной, а координата точки минимума х * должна быть больше 30. Имеем х1 =х0 - D = 35. Далее х2 = х1 + 2 D = 45, f (45) = 3025 < f(х1)
откуда х *>35.
х3 = х2 + 22 D = 65, f (65) = 1225 < f(х2),
откуда х*> 45.
х4 = х3 + 23 D = 105 f (105) = 25 < f(х3),
откуда х*> 65.
х5 = х4 + 24 D = 185, f (185) = 7225 > f(х4)
следовательно, х*< 185. Таким образом, шесть шагов вычислении х* позволили выявить интервал 65£ х *£185, в котором расположена точка х*. Заметим, что эффективность поиска граничных точек непосредственно зависит от величины шага D. Если D велико, то получаем грубые оценки координат граничных точек, и построенный интервал оказывается весьма широким. С другой стороны, если D мало, для определения граничных точек может потребоваться достаточно большой объем вычислений.
Этап уменьшения интервала. После того как установлены границы интервала, содержащего точку оптимума, можно применить более сложную процедуру уменьшения интервала поиска с целью получения уточненных оценок координат оптимума. Величина подынтервала, исключаемого на каждом шаге, зависит от расположения пробных точек х1 и х2 внутри интервала поиска. Поскольку местонахождение точки оптимума априори неизвестно, целесообразно предположить, что размещение пробных точек должно обеспечивать уменьшение интервала в одном и том же отношении. Кроме того, в целях повышения эффективности алгоритма необходимо потребовать, чтобы указанное отношение было максимальным. Подобную стратегию иногда называют минимаксной стратегией поиска.
Метод деления интервала пополам. Рассматриваемый метод позволяет исключать в точности половину интервала на каждой итерации. Иногда этот метод называют трехточечным поиском на равных интервалах, поскольку его реализация основана на выборе трех пробных точек, равномерно распределенных в интервале поиска. Ниже приводится описание основных шагов поисковой процедуры, ориентированной на нахождение точки минимума функции f(x) в интервале (а,b).
Шаг 1. Положить хm =(а+b)/ 2 и L=b-a. Вычислить значение f(xm).
Шаг 2. Положить х1 = а + L /4 и х2 = b - L /4. Заметим, что точки х1, хm, х2 делят интервал (а, b) на четыре равные части. Вычислить значения f(х1) и f(х2).
Шаг 3. Сравнить f(х1) и f(хm).
(1) Если f(х1) < f(хm), исключить интервал (xm, b), положив b=Хт.
Средней точкой нового интервала поиска становится точка х1. Следовательно, необходимо положить xm = х1. Перейти к шагу 5.
(2) Если f(х1) ³ f(хm) перейти к шагу 4.
Шаг 4. Сравнить f(х2) и f(хm).
(1) Если f(х2) < f(хm), исключить интервал (a, хm), положив а = хm. Так как средней точкой нового интервала становится точка х3, положить хm = х2. Перейти к шагу 5.
(2) Если f(х2) ³ f(хm), исключить интервалы (а, х1) и (х2, b). Положить а = х1 и b=х2. Заметим, что хm продолжает оставаться средней точкой нового интервала. Перейти к шагу 5.
Шаг 5. Вычислить L=b-a. Если величина |L| мала, закончить поиск. В противном случае вернуться к шагу 2.
Замечания
1. На каждой итерации алгоритма исключается в точности половина интервала поиска.
2. Средняя точка последовательно получаемых интервалов всегда совпадает с одной из пробных точек х1, х2 или хm, найденных на предыдущей итерации. Следовательно, на каждой итерации требуется не более двух вычислений значения функции.
3. Если проведено n вычислений значения функции, то длина полученного интервала составляет (1/2) n /2 величины исходного интервала.
4. Показано, что из всех методов поиска на равных интервалах (двухточечный, трехточечный, четырехточечный и т. д.) трехточечный поиск, или метод деления интервала пополам, отличается наибольшей эффективностью.
Метод золотого сечения. Из проведенного выше обсуждения методов исключения интервалов и минимаксных стратегий поиска можно сделать следующие выводы.
1. Если количество пробных точек принимается равным двум, то их следует размещать на одинаковых расстояниях от середины интервала.
2. В соответствии с общей минимаксной стратегией пробные точки должны размещаться в интервале по симметричной схеме таким образом, чтобы отношение длины исключаемого подынтервала к величине интервала поиска оставалось постоянным.
3. На каждой итерации процедуры поиска должно вычисляться только одно значение функции в получаемой точке.
Руководствуясь этими выводами, рассмотрим симметричное расположение двух пробных точек на исходном интервале единичной длины, которое показано на рис. 6.50 (выбор единичного интервала обусловлен соображениями удобства). Пробные точки отстоят от граничных точек интервала на расстоянии t. При таком симметричном расположении точек длина остающегося после исключения интервала всегда равна t независимо от того, какое из значений функции в пробных точках оказывается меньшим. Предположим, что исключается правый подынтервал. На рис. 8 показано, что оставшийся подынтервал длины t содержит одну пробную точку. расположенную на расстоянии (1- t) от левой граничной точки.
Для того чтобы симметрия поискового образца сохранялась, расстояние (1- t) должно составлять t -ю часть длины интервала (которая равна t). При таком выборе t следующая пробная точка размещается на расстоянии, равном t -й части длины интервала, от правой граничной точки интервала (рис. 6.51).
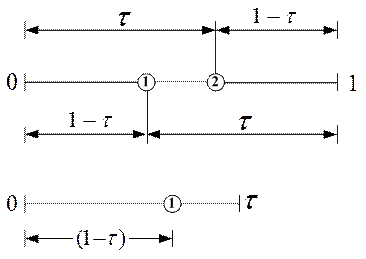
Рис. 6.50 Интервалы, полученные методом золотого сечения
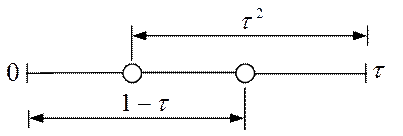
Рис. 6.51 Симметрия золотого сечения интервала
Отсюда следует, что при выборе t в соответствии с условием 1 -t=t2 симметрия поискового образца, показанного на рис.6.50 сохраняется при переходе к уменьшенному интервалу, который изображен на рис.6.51. Решая это квадратное уравнение, получаем
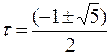 ,
,
откуда положительное решение t =0,61803.... Схема поиска, при которой пробные точки делят интервал в этом отношении, известна под названием поиска с помощью метода золотого сечения. Заметим, что после первых двух вычислений значений функции каждое последующее вычисление позволяет исключить подынтервал, величина которого составляет (1 - t)-ю долю от длины интервала поиска. Следовательно, если исходный интервал имеет единичную длину, то величина интервала, полученного в результате N вычислений значений функции, равна tN-1. Можно показать, что поиск с помощью метода золотого сечения является асимптотически наиболее эффективным способом реализации минимаксной стратегии поиска.
Пример метода золотого сечения
Опять рассмотрим задачу из примера 2.6, в которой требуется минимизировать f(х)=(100- х)2 в интервале 60£ х £150. Для того чтобы перейти к интервалу единичной длины, проведем замену переменной, положив w=(х - 60)/90. Таким образом, задача принимает следующий вид: минимизировать f(w) = (40 – 90 w)2 при ограничении 0£w£1.
Итерация 1. I1 = (0, 1); L1 = l. Проведем два первых вычисления значений функции:
w1 = t = 0,618, f(w1) = 244,0
w2 = 1- t = t 2 = 0,382, f(w2) = 31,6
Так как f(w2) < f(w1) и w2 < w1, интервал w ³ w1 исключается.
Итерация 2. I2 =(0. 0,618); L2 = 0,618 = t. Следующее вычисление значения функции проводится в точке
w3 = t-t2 = t(1-t) = t3 = 0,236, f(w3) = 352.
Так как f(w3) > f (w2) и w3 < w2, интервал w £ w3, исключается.
Итерация 3. I3 =(0,236, 0,618); L3 = 0,382 = t2. Следующее вычисление значения функции проводится в точке, расположенной на расстоянии t ´ (длина полученного интервала) от левой граничной точки интервала, или на расстоянии (1- t) ´ (длина интервала) от правой граничной точки. Таким образом,
w4 =0,618 – ( 1- t)L3 = 0.618 - t2 L3 0.618 - t2(t2) = 0.618 - t4 = 0,472, f(w4) = 6,15.
Так как f(w4) < f (w2) и w4 > w2, интервал w £ w2 исключается.
В результате получен следующий интервал неопределенности: 0,382 £ w £ 0,618 для переменной w, или 94,4£ х £115,6 для переменной х.
Если в процессе поиска проведено шесть вычислений значений функции, то длина результирующего интервала для переменной w равна
tN-1 = t5 = 0,09,
что соответствует интервалу длины 8,1 для переменной х. Для сравнения напомним, что в аналогичной ситуации метод деления интервала пополам привел к получению интервала длины 11,25.
В общем случае если правая и левая граничные точки интервала неопределенности (обозначим их через XR и XL) известны, то координаты всех последующих пробных точек, получаемых в соответствии с методом золотого сечения, можно вычислить по формулам
w = XR - tn или w = XL + tn, в зависимости от того, какой подынтервал был исключен на предыдущей итерации – левый или правый. В приведенных выше формулах через tn обозначена n -я степень t, где п – количество вычислений значений функции.
Поиск с помощью метода золотого сечения может быть окончен либо исходя из заданного количества вычислений значений функции (и, следовательно, величины интервала неопределенности), либо по достижении относительной точности искомого значения функции. Наиболее предпочтительным является использование обоих критериев одновременно.
Сравнение методов исключения интервалов. Ниже проводится сравнение относительных эффективностей рассмотренных методов исключения интервалов. Обозначим длину неходкого интервала неопределенности через L1, а длину интервала, получаемого в результате N вычислений значений функции, - через LN. В качестве показателя эффективности того или иного метода исключения интервалов введем в рассмотрение характеристику относительного уменьшения исходного интервала FR(N)=LN/L1
Напомним, что при использовании метода деления интервала пополам и метода золотого сечения длина получаемого интервала составляет L1(0,5)N/2 и L1(0.618)N-1 соответственно. Следовательно, относительное уменьшение интервала после N вычислений значений функции равно
FR(N) = (0,5)N/2 для метода деления интервала пополам;
FR(N) = (0,618) N-1 для метода золотого сечения.
Для сравнения рассмотрим также метод равномерного поиска, в соответствии с которым оценивание функции проводится в N равноотстоящих друг от друга точках (при этом интервал L1 делится на (N+1) равных интервалов длины L1/(N+l)). Пусть х* – точка, в которой наблюдается минимум функции f(х). Тогда точка истинного минимума f(x) оказывается заключенной в интервале
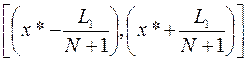 ,
,
откуда LN = 2L1/(N+l). Следовательно, для метода равномерного поиска FR(N)=2/(N+1).
В табл. 6.2 представлены значения FR(N), соответствующие выбранным N, для трех методов поиска. Из таблицы следует, что поиск величины относительного уменьшения интервала с помощью метода золотого сечения
Таблица 6.2
| Метод поиска
| Количество вычислений значений функции
|
| N=2
| N=5
| N=10
| N=15
| N=20
|
| Метод деления интервала пополам
| 0,5
| 0,177
| 0,031
| 0,006
| 0,0009
|
| Метод золотого сечения
| 0,618
| 0,146
| 0,013
| 0,001
| 0,0001
|
| Метод равномерного поиска
| 0,667
| 0,333
| 0,182
| 0,125
| 0,095
|
обеспечивает наибольшее относительное уменьшение исходного интервала при одном и том же количестве вычислений значений функции. С другой стороны, можно также сравнить количества вычислений значения функции, требуемые для достижения заданной величины относительного уменьшения интервала или заданной степени точности. Если величина FR(N) = E задана, то значение N вычисляется по следующим формулам:
для метода деления интервала пополам
N=2 ln(E)/ln(0,5),
для метода золотого сечения
N=1+[ln(E)/ln(0,618)],
для метода равномерного поиска
N=(2/E)-1
В табл. 6.3 приведены данные о количествах вычислений значений функции, необходимых для определения координаты точки минимума с заданной точностью. Следует еще раз подчеркнуть, что метод золотого сечения оказывается более эффективным по сравнению с остальными двумя методами, поскольку он требует наименьшего числа оцениваний значения функции для достижения одной и той же заданной точности.
Требуемые количества вычислений значений функции
Таблица 6.3
| Метод поиска
| Заданная точность
|
| Е=0,1
| Е=0,05
| Е=0,01
| Е=0,001
|
| Метод деления интервала пополам
|
|
|
|
|
| Метод золотого сечения
|
|
|
|
|
| Метод равномерного поиска
|
|
|
|
|
Критерии оптимизации
Важная сторона оптимизации – это выбор критерия, по которому определяются свойства объекта и который позволяет количественно оценить какое из устройств данного класса является наилучшим.
Критерии в зависимости от назначения устройства могут быть самыми разными.
Так при проектировании фильтра критерий может относиться к его амплитудно-частной характеристике, минимуму потерь в полосе прозрачности и максимуму – в полосе заграждения.
В случае усилителя высокочастотных колебаний такой критерий может быть связан с получением максимального КПД, с соблюдением требования по нелинейным искажениям сигнала.
Несмотря на все разнообразие критериев их можно свести к единой математической записи – функции цели, которая в концентрированной форме отражает смысл решаемой задачи по оптимизации устройства – в наилучшем приближении его характеристик к требуемым согласно определенным признакам.
Все действия в такой программе оптимизации в конечном итоге направлены на получение экстремального значения функции цели – максимального или минимального, в зависимости от поставленной задачи.
Поскольку, как правило, качество устройства определяют несколько критериев (например, в приводимом выше примере с фильтром – максимум в одной полосе, минимум – в другой), то целевая функция является суммой определенного числа членов и по своему виду является взвешенно-аддитивно цифровой, отражающей требование минимального отличия желаемых (иногда идеальных) характеристик от реально получаемых. Составим в обобщенном виде функцию цели.
При исследовании в частотной области для целевой функции, определяемой K критериями, запишем:
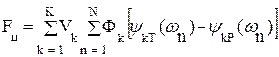 (6.5)
(6.5)
где Фk – частная целевая функция для k-й характеристики;
ψkT – функция, определяющая требуемую k-ю частотную характеристику;
ψkP – функция, определяющая реально полученную k-ю частотную характеристику, зависящую от параметров устройства;
Vk – весовой множитель для k-й характеристики.
Мерой расхождения между требуемой и реальной характеристиками могут являться или минимум суммы квадратов уклонений, или минимаксный критерий. При них функция цели примет вид:
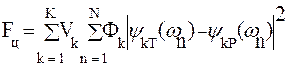 (6.6)
(6.6)
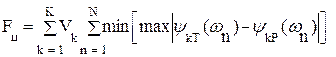 (6.7)
(6.7)
Кроме того возможен вариант, когда требуется получить максимальное отношение параметров устройства, например Ak к Bk. Тогда функция цели примет вид:
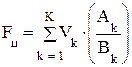 (6.8)
(6.8)
Путем определенной процедуры следует найти или минимальное при (6.6) и (6.7), или максимальное при (6.8) значение функции цели. Для определенности рассмотрим первый случай, связанный с получением минимального значения.
Разделим все параметры устройства, определяющие его реальную характеристику ψkP, на две группы: варьируемые (x1,x2,…,xn) и неизменные (y1,y2,…,ym). Соберем варьируемые параметры (их еще называют переменными) в вектор-столбец, который затем преобразуем в транспонированную матрицу:
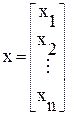
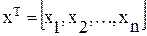 (6.9)
(6.9)
Аналогичным образом поступим с постоянными или неизменными параметрами устройства:
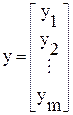
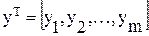 (6.10)
(6.10)
Будем рассматривать вектор x как точку или элемент n-мерного действительного пространства Rn . Совокупность объектов x произвольного содержания (точки, векторы, функции и т.д.) составляют множество X, а сами объекты есть элементы этого множества. Совместив понятия точечного множества, составленного из точек х, и n-мерного пространства Rn , можно утверждать, что множество X представляет собой совокупность точек х в многомерном пространстве Rn .
В процессе поиска среди множества векторов x следует найти такой вектор Xопт в пространстве Rn , при котором функция цели (6.6) или (6.7) минимальна:
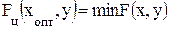 , где x Є Rn (6.11)
, где x Є Rn (6.11)
При этом на вектор х могут накладываться определенные ограничения. Точка xопт соответствует наилучшему в соответствии с выбранными критериями варианту проектируемого устройства. Поиск xопт относится к классу задач, объединяемых теорией нелинейного программирования. При этом вектор х во всех рассматриваемых ниже задачах ограничен определенным пространством Rn , что можно следующим образом представить в развернутом виде:
x1мин ≤ x1 ≤ x1макс, ……….xn.мин ≤ xn.макс (6.12)
При функции цели в виде (6.8) выражение (6.11) примет вид:
Fц (xопт,y)=maxF(x,y), где x Є Rn (6.13)
Перейдем к рассмотрению путей нахождения xопт.







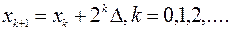


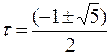 ,
,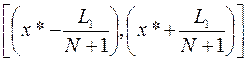 ,
,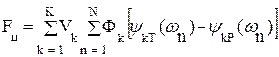 (6.5)
(6.5)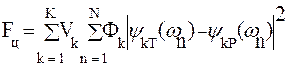 (6.6)
(6.6)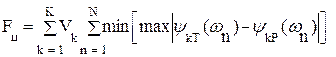 (6.7)
(6.7)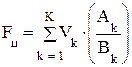 (6.8)
(6.8)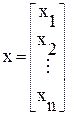
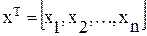 (6.9)
(6.9)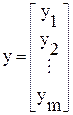
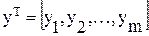 (6.10)
(6.10)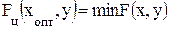 , где x Є Rn (6.11)
, где x Є Rn (6.11)


