На нестационарных отрезках
Пусть независимые переменные — время τ и t — имеют общее начало отсчета, тогда конечный отрезок [а, b]времени τ назовем нестационарным, если хотя бы один конец этого отрезка подвижен, являясь функцией времени t, и стационарным, если оба конца отрезка неподвижны. Функции a(t), b{t) служат характеристиками нестационарного отрезка. Нестационарный отрезок можно описывать также его длиной T(t)= b(t)— a(t) и одной из функций a(t) или b(t). Нестационарный отрезок [ a(t), b(t) ] очерчивает полосу в плоскости
(t, τ), заключенную между кривыми τ = a(t), τ = b (t).
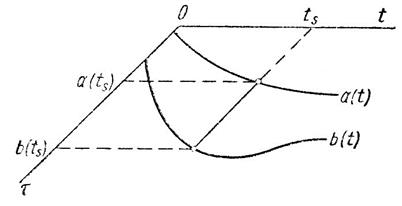
Рисунок - Графическое изображение нестационарного отрезка
Систему функций {ψi (t, τ ) }, определенных на [ a(t), b(t) ], назовем ортогональной на нестационарном отрезке [ a(t), b(t) ] с весом ρ(t, τ), если все функции этой системы удовлетворяют условию

при i ≠ j
Нормы функций, ортогональных на нестационарном отрезке, определяемые выражением
 ,
,
являются функциями времени t.
Систему функций {ψi (t, τ ) }, ортогональную на нестационарном отрезке [ a(t), b(t) ], назовем ортонормированной, если нормы всех функций этой системы постоянны и равны единице. Для функций ортонормированной системы справедливы соотношения и

при i = j
Всякую систему, ортогональную на нестационарном отрезке, не содержащую функций с нулевой нормой, можно нормировать, разделив каждую функцию на ее норму. Если известна система функций, ортогональных на стационарном конечном отрезке
[а, b] (полиномы Якоби, Чебышева, Лежандра, тригонометрические функции т. д.), то легко получить систему функций, ортогональную на нестационарном отрезке [a(t), b(t)], путем формальной замены а и b в явных выражениях стационарных функций и их функций веса на функции
a(t), b(t), описывающие концы нестационарного отрезка.
Пример. Системы нестационарных тригонометрических функций. Запишем лишь две системы, ортонормированные на отрезке [0, t]:


i = 1,2,…, 0 ≤ τ ≤ t,

i = 1,2,…, 0 ≤ τ ≤ t.)
Весовая функция этих систем
ρ (t, τ) = 1.
Нестационарные ортогональные функции могут быть изображены в трехмерном пространстве с координатами ψ, t, τ в виде поверхностей.
Рассмотрим примеры систем функций, ортонормированных на нестационарном отрезке [0, t ]. Вначале приведем системы непрерывных функций. Все эти системы являются бесконечными.
Система нестационарных полиномов Лежандра:
 (1.6)
(1.6)
Выпишем первые восемь полиномов:
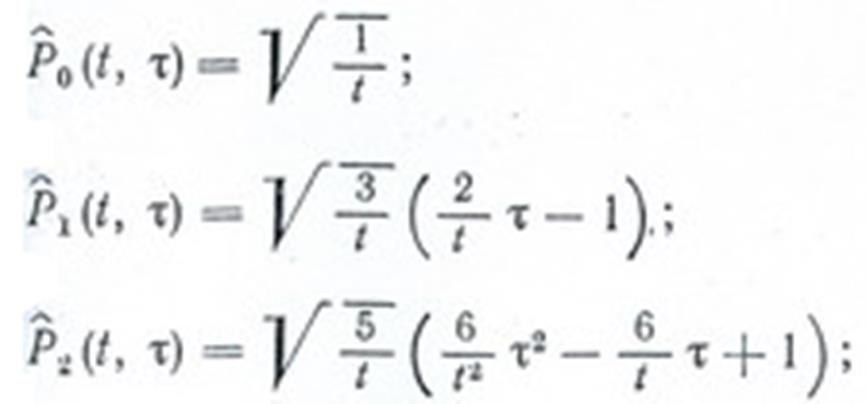

Представление о форме этих полиномов дает рисунок 1.1, где полиномы изображены
для стационарного отрезка [0, 1]:

Рисунок 1.1 – Нестационарные полиномы Лежандра, ортонормированные на отрезке [0, 1] (I = 0, 1, …, 5)
На рисунке 1.1 показан лишь один полином P^2(t, τ) как функция двух аргументов. Естественно, как и любая непрерывная нестационарная ортонормированная функция, этот полином представляется в виде поверхности. Функции, ортогональные на стационарных отрезках являются сечениями таких поверхностей – плоскостями, параллельными плоскости φ, τ.
Системы непрерывных нестационарных тригонометрических функций:

Система непрерывных нестационарных комплексных экспоненциальных функций:
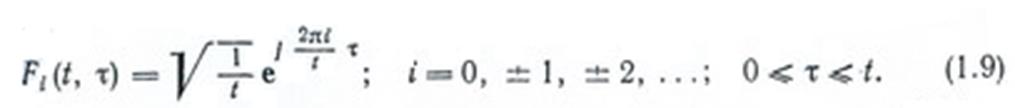
Система непрерывных нестационарных функций Хаара:

Система непрерывных нестационарных функций Уолша (диадно-упорядоченных):

где rn(t, τ) - функция Родемахера:
rn(t, τ) = sign  ; n=0, 1, 2 …;
; n=0, 1, 2 …; 
Приведем теперь системы дискретных нестационарных ортонормированных функций. Предварительно отметим, что некоторые дискретные ортонормированные системы функций могут быть образованы из непрерывных ортонормированных систем путем выборки ординат непрерывных функций в дискретные моменты времени τ 1 с последующей нормировкой получаемых при этом дискретных функций. Часто выборка может быть равномерной, т. е. τ 1 = τ0 + IT, где l = 0, 1..., L — 1. Такое построение возможно, например, для системы нестационарных тригонометрических функций, комплексных экспоненциальных функций, функций Хаара и Уолша. Системы дискретных нестационарных ортонормированных функций, определенные на конечном отрезке времени, являются конечными. Число функций этих систем равно числу L отсчетов дискретного времени в пределах упомянутого конечного отрезка.
Системы дискретных нестационарных тригонометрических функций:

Система дискретных нестационарных комплексных экспоненциальных функций:

Обратим внимание, что число тактовых моментов L, на которых определена базисная система, должно быть обязательно четным.
Система дискретных нестационарных функций Хаара:

Система дискретных нестационарных функций Уолша (диадно-упорядоченных):

где rn(L, l) – дискретные функции Родемахера.
rn(L, l) = sign 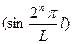 ; L = 2p+1; p = 0, 1, …; n=0, 1, …, p; l = 0, 1, …, L-1;
; L = 2p+1; p = 0, 1, …; n=0, 1, …, p; l = 0, 1, …, L-1;
Нужно обратить внимание, что дискретные функции Хаара и Уолша определяются на числе точек дискретного времени, равном целой степени числа 2.
Система дискретных нестационарных полиномов Чебышева:

i = 0, 1, …,L-1; l = 0, 1, …, L-1, где l [ν] = l(l -1) … (l – ν + 1)
Выпишем первые четыре полинома этой системы:

Имея в виду, что  ,
,  и, устремляя T к нулю, формулы (1.14) можно привести к выражению (1.16), которое описывает непрерывные нестационарные полиномы Лежандра.
и, устремляя T к нулю, формулы (1.14) можно привести к выражению (1.16), которое описывает непрерывные нестационарные полиномы Лежандра.
Система одиночных импульсов:
 ; i, l = 0, 1, …, L-1, (1.15)
; i, l = 0, 1, …, L-1, (1.15)
где 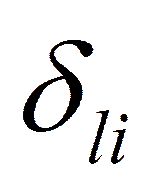 - символ Кронекера;
- символ Кронекера;  - дискретная дельта-функция.
- дискретная дельта-функция.
Все приведенные выше дискретные ортонормированные функции являются функциями номера дискретного момента времени l и числа этих моментов L в пределах отрезка [0, t]. Поэтому в пределах отрезка [0, t] дискретные функции могут быть связаны с любой последовательностью тактовых моментов: как равноотстоящих, так и неравноотстоящих друг от друга; сдвинутых или несдвинутых относительно начальной точки. Огибающие дискретных функций, полученных из непрерывных путем выборок в равнотстоящих точках, но привязанных к другой системе тактовых моментов, будут не совпадать с этими непрерывными функциям.
Понятие функций, ортонормированных на нестационарном отрезке, естественно обобщается на случай ортогональности в прямоугольнике и в областях с числом измерений больше двух. Функции практически используемых систем строят как произведения функций, ортонормированных на нестационарных отрезках, образующих заданную область. Например, система функций {φhi (t1, τ1, t2, τ2)}, ортонормированная на прямоугольнике 0≤ τ1 ≤ t1, 0 ≤ τ2≤ t2, образуется следующим образом:
φhi (t1, τ1, t2, τ2) = qh(t1, τ1)pi*(t2, τ2),
где { qh(t1,τ1)} – система функций, ортогональных на отрезке [0, t1], а {pi*(t2, τ2)} – система функций, ортогональных на отрезке [0, t2].
В качестве систем {pi}, {qh} можно использовать, например, приведенные выше нестационарные полиномы Лежандра, тригонометрические и комплексные функции, кусочные постоянные функции. Функции pi, qh могут быть как однотипным, так и разных типов, например, pi— полиномы Лежандра, a qh - тригонометрические функции. Обе системы функций pi и qh могут быть непрерывными либо дискретными, либо одна непрерывная, другая дискретная, например:
φhi (t, τ, L, l) = qh(t, τ)pi*(L, l).

|
| Дата рождения:
| 4 (16) мая 1821(18210516)
|
| Место рождения:
| Окатово, Калужская губерния, Российская империя
|
| Дата смерти:
| 8 (26) декабря 1894
|
| Место смерти:
| Санкт-Петербург, Российская империя
|
| Научная сфера:
| математика
|
| Место работы:
| Петербургский университет
|
| Научный руководитель:
| Николай Дмитриевич Брашман
|
| Знаменитые ученики:
| А. М. Ляпунов Е. И. Золотарёв
|
| Известен как:
| один из основателей современной теории приближений
|







 ,
,



 (1.6)
(1.6)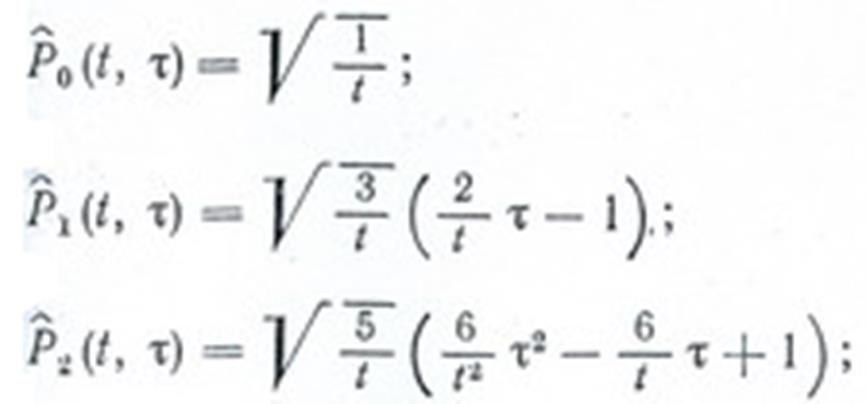



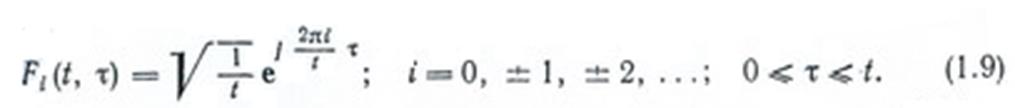


 ; n=0, 1, 2 …;
; n=0, 1, 2 …; 




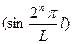 ; L = 2p+1; p = 0, 1, …; n=0, 1, …, p; l = 0, 1, …, L-1;
; L = 2p+1; p = 0, 1, …; n=0, 1, …, p; l = 0, 1, …, L-1;

 ,
,  и, устремляя T к нулю, формулы (1.14) можно привести к выражению (1.16), которое описывает непрерывные нестационарные полиномы Лежандра.
и, устремляя T к нулю, формулы (1.14) можно привести к выражению (1.16), которое описывает непрерывные нестационарные полиномы Лежандра. ; i, l = 0, 1, …, L-1, (1.15)
; i, l = 0, 1, …, L-1, (1.15)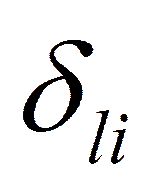 - символ Кронекера;
- символ Кронекера;  - дискретная дельта-функция.
- дискретная дельта-функция.


