 .
.
Значимость фи-коэффициента определяется с помощью критерия  (хи-квадрат):
(хи-квадрат):
 .
.
Если вычисленное значение  меньше табличного с одной степенью свободы, то нулевая гипотеза об отсутствии устойчивости пункта не отвергается (т.е. пункт признается неустойчивым).
меньше табличного с одной степенью свободы, то нулевая гипотеза об отсутствии устойчивости пункта не отвергается (т.е. пункт признается неустойчивым).
Использование фи-коэффициента удобно потому, что он одновременно оценивает степень оптимальности данного пункта теста по силе вопроса или трудности задания.
трудность задания – хар-ка, отражающая статистический уровень его решаемости в конкретной выборке стандартизации. 2 вида трудности: субъективно – психологическая; статистическая.
1) субъективно-психологическую (связана с индивидуально-психологическим барьером, величина которого определяется как обстоятельствами,так и уровнем формирования необходимых для решений знаний, умений и навыков, психическим состоянием испытуемого и рядом других факторов.)
2) статистическую(объективную)трудности.
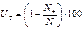 ,
,
где UT – индекс трудности в процентах, N + – число испытуемых, правильно решивших задание, N – общее число испытуемых.
В тестах типа "Выбор" с несколькими вариантами ответов испытуемый может случайно угадать правильный ответ. Для учета такого случайного успеха используется формула:
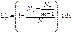
где N – – число испытуемых, не решивших задание,
m – количество вариантов ответа (например, в сериях С–Е теста Равена m = 8).
В случаях, когда велики выборка стандартизации (больше 100 испытуемых) и количество пунктов теста, индекс трудности определяется с помощью сопоставления контрастных (крайних) подгрупп.
Необходимо отметить, что чем больше значение индекса трудности, тем статистическая трудность задания выше, и наоборот. (оптимально=50)
Здесь необходимо отметить, что статистическая трудность задания является относительной характеристикой, т.к. зависит от особенностей выборки (ее возрастных, профессиональных, социокультурных и других различий).
Остановимся на вопросе упорядочивания отдельных заданий в тесте. Обычно если задание решают большинство испытуемых из выборки стандартизации, его (как легкое) помещают в начале теста. Если же задание решает незначительный процент испытуемых, то его (как трудное) помещают в конце теста. Одну-две самые легкие задачи ставят перед основными заданиями теста и используют в качестве примера.
Дискриминативность,- показатель согласованности пункта с тестом. В качестве меры соответствия успешности выполнения одной задачи (пункта) всему тесту в психодиагностике используются:
1) коэффициент дискриминативности данного пункта теста;
2) индекс дискриминации пункта;
3) четырехпольный коэффициент корреляции.
Коэффициент дискриминативности отдельного пункта равен коэффициенту корреляции между средним результатом анализируемого пункта (по принципу правильного/неправильного ответа или совпадения с ключом) и среднимпервичным результатом по всем пунктамтеста. То есть коэффициент дискриминативности учитывает амплитуду отклонения индивидуальных суммарных баллов от среднего балла.
Из множества известных коэффициентов корреляции наиболее точной мерой оказался точечно-биссериальный коэффициент корреляции:
 ,
,
где  – среднее арифметическое всех индивидуальных оценок по всему тесту (средний балл по всем испытуемым);
– среднее арифметическое всех индивидуальных оценок по всему тесту (средний балл по всем испытуемым);
 – среднее арифметическое оценок по тесту у испытуемых, правильно выполнивших задание / показавших совпадение с "ключом";
– среднее арифметическое оценок по тесту у испытуемых, правильно выполнивших задание / показавших совпадение с "ключом";
sх – среднеквадратичное отклонение индивидуальных оценок всех испытуемых выборки по всему тесту;
N + – число испытуемых, правильно решивших анализируемую задачу (или тех, чей ответ на данный пункт опросника соответствует "ключу");
N – общий объем выборки.(>200)
Если <200:
 ,
,
где 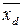 – среднее арифметическое индивидуальных оценок испытуемых, выпол- нивших данное задание;
– среднее арифметическое индивидуальных оценок испытуемых, выпол- нивших данное задание;
sхd – среднеквадратичное отклонение индивидуальных оценок испытуемых, выполнивших данное задание;
Nd – общее число испытуемых, выполнивших данное задание.
Коэффициент дискриминативности, как и любой коэффициент корреляции, может принимать значения от –1 до +1. Высокие положительные значения этого коэффициента свидетельствуют об эффективности деления испытуемых; высокие отрицательные значения – о непригодности данного пункта для теста.
Задачи, характеризующиеся средней трудностью (около 50), обладают высокой дискриминативной способностью.
Индекс дискриминации D отдельного пункта теста вычисляется как разность между долей лиц, правильно решивших данную задачу (показавших совпадение с "ключом"),из "высокопродуктивной" и "низкопродуктивной" групп. Каждая из контрастных групп включает в себя по 27 % испытуемых от численности выборки, имеющих соответственно лучшие и худшие результаты по тесту в целом:
 ,
,
где  ,
,  – числа испытуемых, выполнивших данное задание в "высокой" и "низкой" контрастных группах;
– числа испытуемых, выполнивших данное задание в "высокой" и "низкой" контрастных группах;
 ,
,  – объемы контрастных групп.
– объемы контрастных групп.
Наконец, для оценки дискриминативности можно воспользоваться четырехпольным коэффициентом корреляции:
|
| Высокая
| Низкая
|
| Да
| А
| В
|
| Нет
| C
| D
|
В первом столбце таблицы суммируются ответы испытуемых из "высокой" группы (при нормальном распределении – это "верхние" 27 %), во втором столбце – из "низкой" (нижние 27 %). Четырехпольный коэффициент корреляции рассчитывается по следующей формуле.
Если a > b:  ;
;
Если a < b:  .
.
Критические значения этого коэффициента, свидетельствующие о диагностической ценности пункта, вычисляются по формуле хи-квадрат:  и проверяются для одной степени свободы.
и проверяются для одной степени свободы.
Вопрос 42.





 .
. (хи-квадрат):
(хи-квадрат): .
.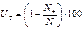 ,
,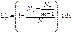
 ,
, – среднее арифметическое всех индивидуальных оценок по всему тесту (средний балл по всем испытуемым);
– среднее арифметическое всех индивидуальных оценок по всему тесту (средний балл по всем испытуемым); – среднее арифметическое оценок по тесту у испытуемых, правильно выполнивших задание / показавших совпадение с "ключом";
– среднее арифметическое оценок по тесту у испытуемых, правильно выполнивших задание / показавших совпадение с "ключом"; ,
,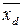 – среднее арифметическое индивидуальных оценок испытуемых, выпол- нивших данное задание;
– среднее арифметическое индивидуальных оценок испытуемых, выпол- нивших данное задание; ,
, ,
,  – числа испытуемых, выполнивших данное задание в "высокой" и "низкой" контрастных группах;
– числа испытуемых, выполнивших данное задание в "высокой" и "низкой" контрастных группах; ,
,  – объемы контрастных групп.
– объемы контрастных групп. ;
; .
. и проверяются для одной степени свободы.
и проверяются для одной степени свободы.


