Тема 10
ТЕМПЕРАТУРНЫЕ ЭФФЕКТЫ РЕАКТИВНОСТИ РЕАКТОРА
Ранее была получена зависимость для характеристики действительных размножающих свойств теплового реактора – эффективного коэффициента размножения:
 (10.1)
(10.1)
а также качественно проанализированы зависимости всех компонентов правой части этого выражения от температуры. Мы видели, что одни из этих температурных зависимостей возрастающие, другие – убывающие, и все они непохожи друг на друга и с изменением температуры меняются в разной степени. Но если каждый из компонентов формулы – сложная функция температуры, то вся их комбинация (10.1) – также является функцией температуры и, наверняка, ещё более сложной. А это значит, что величина реактивности реактора
 (10.2)
(10.2)
также является сложной функцией температуры активной зоны реактора.
Поэтому, если представить себе, что реактор запускается (то есть приводится из подкритического состояния в критическое, в котором kэ = 1, а r = 0) при так называемой комнатной температуре (t = 20 oC), то ясно, что при дальнейшем разогреве реактор перестанет быть критичным, то есть его реактивность перестанет быть нулевой величиной. А раз так, то при r > 0 реактор с разогревом без всяких внешних воздействий будет увеличивать свою мощность, а при r < 0 – наоборот – снижать её. Ясно, что зависимость величины реактивности r(t), появляющейся за счёт изменения температуры в активной зоне реактора, не может не интересовать оператора при управлении реакторной установкой. Реагировать на любые изменения реактивности реактора, компенсировать их введением равных величин реактивностей противоположного знака для поддержания постоянного уровня мощности реактора – это как раз его (оператора) профессиональный удел (при дистанционном управлении реактором) или удел системы автоматики управления мощностью (при автоматическом режиме управления).
Поэтому наш практический интерес к температурному влиянию на величину реактивности реактора так или иначе сводится к получению ответа на аналитический вопрос: как зависит величина реактивности реактора от температуры его активной зоны?
В практике эксплуатации реакторов влияние температуры на реактивность реактора оценивается с помощью двух ключевых понятий – температурный эффект реактивности (ТЭР) и температурный коэффициент реактивности реактора (ТКР).
Температурный эффект и температурный коэффициент реактивности
Познакомимся вначале с этими понятиями применительно к энергетическим ВВР относительно небольшой (< 200 МВт) тепловой мощности с низкотемпературной топливной композицией (работающей при средних температурах не выше 600оС) при постоянной величине расхода теплоносителя в первом контуре. Для таких реакторов, как убедимся далее, понятия ТЭР и ТКР являются более однозначными и менее сложными, чем в больших реакторах энергоблоков АЭС.
Устойчивость энергетического реактора – это его способность при случайных возмущениях реактивности постоянной величины переходить в критическое состояние на новом уровне мощности, а после снятия возмущения – возвращаться в критическое состояние на исходном уровне мощности.
Рассмотрим, какие процессы происходят в реакторе после воздействия на него случайных возмущений реактивности постоянной величины, и за счёт чего обеспечивается столь важное для нас свойство его устойчивости.
Возьмём для рассмотрения любой конкретный реактор, характеризуемый определённой кривой ТЭР (например, кривой III типа). Допустим, что такой реактора разогрет до номинальной средней температуры и работает в критическом режиме (kэ = 1, r = 0) на небольшом уровне мощности Np0, и в некоторый момент он получает случайное возмущающее воздействие положительной реактивности r (t) = idem = r* постоянной величины.
Сообщение реактору r* > 0, разумеется, делает изначально критический реактор надкритическим, то есть его мощность начинает расти. При постоянном расходе охлаждающего активную зону теплоносителя в силу законов теплопередачи с ростом мощности начинает расти средняя температура теплоносителя в реакторе.
 r(t)
r(t)
r*
D rt r S(t) = r* - D rt
0 t
Np(t)
Np1
Np0
0 t
t т(t)
t т D rt = r*
t т1
D rt
t т0 t т0
0 t
rt (t т)
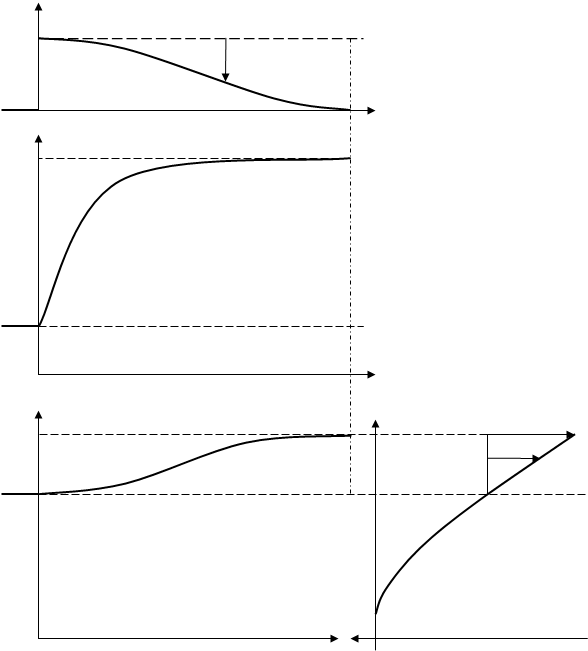
Рис.10.2. Переходные процессы изменений реактивности, тепловой мощности и средней температуры
теплоносителя в реакторе с отрицательным ТКР после возмущения положительной реактивностью r *.
*) Расположенная в правом нижнем углу кривая ТЭР ради более наглядной согласованности с графиком переходного процесса изменений средней температуры теплоносителя повёрнута под углом 90о.
По мере роста мощности и средней температуры растёт величина отрицательного температурного изменения реактивности реактора, которая по мере своего увеличения всё более и более уменьшает суммарную величину положительной реактивности, сообщённой реактору:
r S = r* - D rt.
Следовательно, в процессе роста мощности и средней температуры когда-то должен наступить такой момент, когда отрицательные температурные потери реактивности D rt. сравняются по абсолютной величине с величиной положительной реактивности r*, первоначально сообщённой реактору, и величина суммарной воздействующей на реактор реактивности стане равной нулю. То есть реактор станет критичным на достигнутом к этому моменту уровне мощности, и дальнейший рост мощности и связанный с ним рост средней температуры теплоносителя прекратятся.
Таким образом, первый признак устойчивости реактора, упомянутый в её определении, выполнен, и из проделанных рассуждений следует, что этим свойством реальный реактор обязан тому, что в процессе роста его мощности и средней температуры в нём вырабатывается отрицательная реактивность температурного происхождения, которая постепенно «съедает» величину положительного возмущения сообщённой реактору реактивности r*.
А теперь посмотрим, как обстоит дело с выполнением второго признака устойчивости, а именно – с возвращением реактора на первоначальный уровень мощности после снятия величины положительного возмущения r*.
Теперь, когда реактор критичен на мощности Np1 (то есть его реактивность равна нулю), снять положительную реактивность r* - это то же самое, что сообщить реактору отрицательную реактивность такой же величины. И вряд ли стоит рисовать систему графиков, подобную изображённым на рис.10.2, чтобы сообразить, что все переходные процессы изменений реактивности, мощности и средней температуры будут происходить в обратной последовательности. Сообщение первоначально критичному на мощности Np1 отрицательной реактивности (- r*) делает реактор подкритическим, в результате чего он начинает снижать нейтронную и тепловую мощность. Снижение мощности при постоянном расходе теплоносителя приведёт к уменьшению средней температуры теплоносителя, что, в свою очередь, приведёт к температурному высвобождению положительной реактивности, которая, алгебраически складываясь с отрицательной реактивностью (- r*), приводит к всё большему и большему уменьшению абсолютной величины суммарной реактивности r S, которое неминуемо закончится тем, что последняя упадёт до нуля (при возрастании D rt до |- r* |), и это случится именно в тот момент, когда мощность реактора и средняя температура теплоносителя в нём снизятся до исходных значений (Np0 и tт0 соответственно).
Теперь вернёмся к условию устойчивости реактора. Для приведенных рассуждений была взята кривая ТЭР реального реактора III типа, но с таким же успехом можно было бы взять кривую ТЭР I или II типа. Для кривых ТЭР всех трёх типов характерным является то, что все они имеют в зоне рабочих средних температур теплоносителя убывающий характер.
А если бы было по-иному? Если бы кривая ТЭР имела в этой зоне восходящий вид?
- При сообщении первоначально критическому реактору положительного возмущения r* реактор, становясь надкритическим, увеличивает мощность и среднюю температуру теплоносителя. С ростом температуры при возрастающем характере кривой ТЭР начинает высвобождаться температурная положительная реактивность D rt, которая, добавляясь к величине r*, увеличивает суммарную величину воздействующей на реактор положительной реактивности. Реактор начинает увеличивать мощность и среднюю температуру всё более и более возрастающим темпом, что приведёт к ещё большему темпу высвобождения положительной температурной реактивности, а последняя – к ещё большему темпу роста мощности и средней температуры… Чем это может без вмешательства человека закончиться – нетрудно себе представить: активная зона от перегрева твэлов будет разрушена. Реактор с такой кривой ТЭР, конечно же, не будет устойчивым. Приводя три характерных для энергетических ВВР кривых ТЭР, мы не делали замечаний о том, что кривая ТЭР принципиально может иметь и чисто восходящий характер. Потому, что, как теперь должно быть ясно, реактор с такой температурной характеристикой попросту не имеет право на существование.
Следовательно:
Условием устойчивости энергетического реактора является падающий характер кривой ТЭР в зоне рабочих средних температур или (выражаясь более профессионально) – отрицательность величины ТКР в этой зоне.
Конечно, обеспечить отрицательность и оптимальную величину ТКР реактора в течение всей кампании – задача конструкторов-расчётчиков активной зоны. Удел эксплуатационников – следить в течение всей кампании за тем, чтобы величина отрицательного ТКР не вышла за определённые пределы. Потому, что даже отрицательность величины ТКР в зоне рабочих средних температур не даёт гарантий обеспечения практической устойчивости работы реактора, которая определяется не только знаком ТКР (отрицательность ТКР – это только необходимое условие устойчивости), но и его абсолютной величиной.
Величина ТКР не может быть слишком малой. Какой смысл говорить о принципиальной устойчивости реактора, который при умеренном положительном возмущении r* = 0.15% прекратит увеличение мощности лишь тогда, когда она достигнет 200% от номинальной, а средняя температура теплоносителя вырастет выше 350 оС? Такой реактор без внешнего вмешательства в его работу (со стороны оператора или системы автоматического регулирования мощности – безразлично) опасен почти так же, как и реактор с положительным температурным коэффициентом реактивности. Поэтому малый по абсолютной величине отрицательный ТКР явно недостаточен для обеспечения практической устойчивости реактора.
Предположим далее, что удалось создать реактор с очень большим по абсолютной величине отрицательным ТКР в зоне рабочих температур. В этом случае увеличение средней температуры даже на 2 – 3 оС сопряжено с появлением большой температурной отрицательной реактивности, а, значит, даже для небольшого повышения мощности реактора потребуется затрачивать для компенсации этих потерь реактивности большие величины оперативного запаса реактивности реактора. Значит, и большой отрицательный ТКР – не хороший фактор, сковывающий маневренные свойства реактора. Но и это ещё – полбеды: в определённых условиях большой отрицательный ТКР может стать источником ядерной опасности. Достаточно представить себе ситуацию, связанную с резким охлаждением активной зоны (например, за счёт «заброса» в реактор относительно холодного теплоносителя): в результате резкого (даже небольшого по величине) падения средней температуры в активной зоне в этом случае будет практически без запаздывания высвобождена большая величина положительной реактивности, причём в течение столь малого промежутка времени, что введением подвижных поглотителей в активную зону скомпенсировать эту реактивность можно, попросту говоря, не успеть.
Следовательно, абсолютная величина отрицательного ТКР в зоне рабочих температур должна быть не малой и не большой, она должна быть оптимальной для данного типа реактора с учётом оперативных возможностей его органов СУЗ, требующейся для практики использования РУ маневренности, располагаемого оперативного запаса реактивности и некоторых других факторов.
Ещё раз подчеркнём то, о чём не имеет права забывать оператор РУ: обеспеченный в начале кампании отрицательный ТКР изменяет свою величину в процессе кампании. Значит, для того, чтобы пользоваться в расчётах достоверными данными, необходимо с должной регулярностью проводить физические измерения и уточнять температурные характеристики реактора.
Наконец, несмотря на обеспеченный расчётчиками отрицательный ТКР, для того, чтобы не выйти за пределы устойчивости, следует ограничивать величины разовых введений положительных реактивностей. Реактор – не ванька-встанька, способный подняться в вертикальное положение после толчка любой силы; чем меньшие по величине толчки положительных реактивностей он испытывает, тем лучше для него во всех отношениях. И, в первую очередь, - в отношении устойчивости его работы.
ТЭР и ТКР теплоносителя
Во всём диапазоне изменений средней температуры теплоносителя – от 20оС до наибольшей температуры рабочей зоны – изменение реактивности ВВЭР происходит за счёт изменений ядерных свойств теплоносителя (микросечений поглощения воды и содержащейся в ней борной кислоты) и изменений плотности воды, которые, кстати имеют место не только с изменением температуры воды, но и давления в реакторе.
Ранее (п.10.4.2) упоминалось, что законы передачи тепла от топлива к теплоносителю на разных уровнях мощности реактора ставят в более или менее жёсткое соответствие величины средних температур топлива и теплоносителя:
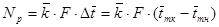 .
.
Следовательно, соотношение мощности и средней температуры теплоносителя
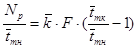
определяется в конкретном реакторе соотношением средних температур топливной композиции и теплоносителя ( ), которое опять-таки определяется только тепловой мощностью реактора. А, значит, величину полного ТЭР (ТКР) реактора принципиально можно было бы поставить в соответствие с величиной уровня мощности. Чего, к сожалению, не получается, потому что:
), которое опять-таки определяется только тепловой мощностью реактора. А, значит, величину полного ТЭР (ТКР) реактора принципиально можно было бы поставить в соответствие с величиной уровня мощности. Чего, к сожалению, не получается, потому что:
- во-первых, одна и та же величина тепловой мощности реактора
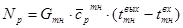
может обеспечиваться при различных комбинациях расходов теплоносителя Gтн и подогревов его в активной зоне ( ), а, значит, в этих комбинациях (учитывая нелинейный характер роста температуры теплоносителя от входа к выходу активной зоны) будет меняться и средняя температура теплоносителя
), а, значит, в этих комбинациях (учитывая нелинейный характер роста температуры теплоносителя от входа к выходу активной зоны) будет меняться и средняя температура теплоносителя  , не говоря уже о среднеэффективной температуре активной зоны;
, не говоря уже о среднеэффективной температуре активной зоны;
- во-вторых, величины средних температур топлива и теплоносителя зависят от характера распределения энерговыделения по высоте реактора, а, значит, и от характера вертикальной составляющей нейтронного поля в активной зоне (а это – довольно изменчивая в процессе кампании характеристика).
Именно эта неоднозначность зависимости r(Np), её изменчивость в различных условиях эксплуатации реактора вынуждает пользоваться в физических расчётах различными составляющими ТЭР (ТКР). Потребность в расчётах при различных расходах теплоносителя, при различных средних температурах теплоносителя и в различные моменты кампании активной зоныдиктует потребность в точном знании таких составляющих ТЭР (ТКР), которые можно было бы корректно измерить в рабочих условиях эксплуатации реактора.
С этой целью весь ТЭР (ТКР) ВВЭР с высокотемпературным топливом делят на две материальные составляющие - ТЭР (ТКР) топлива и ТЭР (ТКР) теплоносителя.
Температурный эффект топлива проявляется при температурах топлива, существенно превышающих величины средних температур теплоносителя, что в условиях реальной эксплуатации ВВЭР имеет место при работе реактора на мощности. Поэтому учитывать изменения реактивности, обусловленные только температурой топлива, во всех отношениях удобнее не как функцию изменения средней температуры топлива (последнюю рассчитывать достаточно непросто), а как функцию изменения величины мощности реактора. То есть как мощностные изменения реактивности, о чём говорилось в п.10.5.
Температурный эффект теплоносителя проявляется при разогреве теплоносителя от 20 оС вплоть до самых больших средних его температур. Теоретически он действует независимо от температурного эффекта топлива, если в процессе разогрева теплоносителя сохраняется неизменной средняя температура топлива. При реальной эксплуатации реактора его действие можно проследить и зафиксировать в процессе очень медленного разогрева критического на МКУМ реактора от постороннего источника тепла. Именно так производится измерение температурного коэффициента реактивности теплоносителя: разогрев со скоростью не более 10 оС/час при поддержании реактора на МКУМ гарантирует непревышение средней температуры топлива над средней температурой теплоносителя и практически нулевое мощностное изменение реактивности реактора.
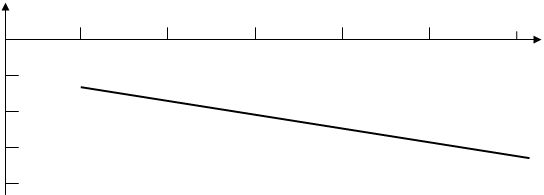
Температурный коэффициент реактивности теплоносителя (at) в наиболее важном интервале средних температур теплоносителя – выше 278оС – отрицателен и с ростом температуры увеличивается по абсолютной величине приблизительно по линейному закону (рис.10.5).
 at, %/оС
at, %/оС
275 280 285 290 295 300
t,o
- 0.010
- 0.015
- 0.020
- 0.025
Рис. 10.5. Зависимость ТКР теплоносителя ВВЭР-1000 в интервале температур 275 – 300оС.
До температуры 279 – 280оС разогрев ВВЭР-1000 обеспечивается за счёт джоулева тепла от работающих ГЦН. Выше этой температуры реактор разогревается собственным («ядерным») теплом. Поэтому экспериментально в начале кампании определяется минимальная величина ТКР теплоносителя именно при этой температуре.
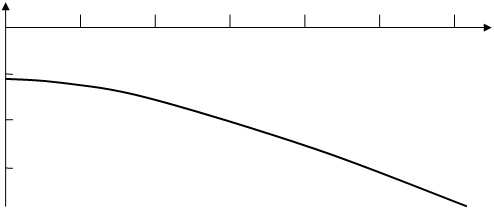
В распоряжении оператора всегда имеется расчётная кривая ТКР теплоносителя при номинальной средней температуре теплоносителя в различные моменты кампании (в зависимости от величины энерговыработки W), качественный вид которой показан на рис.10.6.
 50 100 150 200 250 300 W, эф.сут
50 100 150 200 250 300 W, эф.сут
- 0.02
- 0.04
- 0.06
Рис.10.6. Изменение ТКР теплоносителя при номинальной средней температуре в процессе кампании.
Таким образом, совместное изменение реактивности за счёт изменений мощности реактора и средней температуры теплоносителя (в пределах указанного интервала) найдётся как
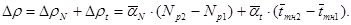 (10.6.1)
(10.6.1)
Для получения корректных результатов расчёта значения МКР и ТКР теплоносителя желательно усреднять для интервалов изменения мощности реактора и средней температуры теплоносителя соответственно.
Тема 10
ТЕМПЕРАТУРНЫЕ ЭФФЕКТЫ РЕАКТИВНОСТИ РЕАКТОРА
Ранее была получена зависимость для характеристики действительных размножающих свойств теплового реактора – эффективного коэффициента размножения:
 (10.1)
(10.1)
а также качественно проанализированы зависимости всех компонентов правой части этого выражения от температуры. Мы видели, что одни из этих температурных зависимостей возрастающие, другие – убывающие, и все они непохожи друг на друга и с изменением температуры меняются в разной степени. Но если каждый из компонентов формулы – сложная функция температуры, то вся их комбинация (10.1) – также является функцией температуры и, наверняка, ещё более сложной. А это значит, что величина реактивности реактора
 (10.2)
(10.2)
также является сложной функцией температуры активной зоны реактора.
Поэтому, если представить себе, что реактор запускается (то есть приводится из подкритического состояния в критическое, в котором kэ = 1, а r = 0) при так называемой комнатной температуре (t = 20 oC), то ясно, что при дальнейшем разогреве реактор перестанет быть критичным, то есть его реактивность перестанет быть нулевой величиной. А раз так, то при r > 0 реактор с разогревом без всяких внешних воздействий будет увеличивать свою мощность, а при r < 0 – наоборот – снижать её. Ясно, что зависимость величины реактивности r(t), появляющейся за счёт изменения температуры в активной зоне реактора, не может не интересовать оператора при управлении реакторной установкой. Реагировать на любые изменения реактивности реактора, компенсировать их введением равных величин реактивностей противоположного знака для поддержания постоянного уровня мощности реактора – это как раз его (оператора) профессиональный удел (при дистанционном управлении реактором) или удел системы автоматики управления мощностью (при автоматическом режиме управления).
Поэтому наш практический интерес к температурному влиянию на величину реактивности реактора так или иначе сводится к получению ответа на аналитический вопрос: как зависит величина реактивности реактора от температуры его активной зоны?
В практике эксплуатации реакторов влияние температуры на реактивность реактора оценивается с помощью двух ключевых понятий – температурный эффект реактивности (ТЭР) и температурный коэффициент реактивности реактора (ТКР).





 (10.1)
(10.1) (10.2)
(10.2) r(t)
r(t)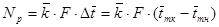 .
.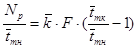
 ), которое опять-таки определяется только тепловой мощностью реактора. А, значит, величину полного ТЭР (ТКР) реактора принципиально можно было бы поставить в соответствие с величиной уровня мощности. Чего, к сожалению, не получается, потому что:
), которое опять-таки определяется только тепловой мощностью реактора. А, значит, величину полного ТЭР (ТКР) реактора принципиально можно было бы поставить в соответствие с величиной уровня мощности. Чего, к сожалению, не получается, потому что: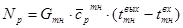
 ), а, значит, в этих комбинациях (учитывая нелинейный характер роста температуры теплоносителя от входа к выходу активной зоны) будет меняться и средняя температура теплоносителя
), а, значит, в этих комбинациях (учитывая нелинейный характер роста температуры теплоносителя от входа к выходу активной зоны) будет меняться и средняя температура теплоносителя  , не говоря уже о среднеэффективной температуре активной зоны;
, не говоря уже о среднеэффективной температуре активной зоны; at, %/оС
at, %/оС
 50 100 150 200 250 300 W, эф.сут
50 100 150 200 250 300 W, эф.сут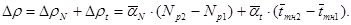 (10.6.1)
(10.6.1)


