Определение общего, частного решения ОДУ, общего интеграла, интеграла ОДУ

Определение порядка оду

Наивысший порядок производной в ходящий в оду называется порядком этого уравнения

 

Формы записи оду

1) Оду разрешённые относительно старшей производной

2) Оду не разрешённые относительно старшей производной

3) Оду в диффиринциальной форме (dy=(x²+y²)dx)

 

Определение решиния ОДУ

Решение оду называется функия которая при подстановке в уравнение обращает его в тождество

 

Определение общего, частного решения ОДУ, общего интеграла, интеграла ОДУ

1) Общее решение-если оно представляет собой явно заданную функцию, содержащую произвольные постоянные

2) Частное решение-представляет собой явную функцию, не содержащую произвольные постоянные

3) Общий интеграл представляет собой не явно заданную функцию, содержащую const

4) Интеграл представляет собой не явно заданную функцию, не содержащую произвольные const

 

Определение задачи коши

Задача нахождения решения ОДУ, которая добавляет дополнительное условие называется задачей коши, а дополнительное условие называется начальным

 

Существование решения задачи коши.

1) Теорема коши: Пусть y^’=f(x,y)

                                    y(x₀)=y₀, если f(x,y) непрерывна и имеет непрерывную, частную производную по переменной Y, в некоторой области (D принадлежит R²), то какова бы не была точка (x₀,y₀) (из начального условия) задача Коши в этой области имеет единственное решение

2) Теорема Пикара: Пусть y^’=f(x,y)

                                        y(x₀)=y₀, если f(x,y) непрерывна в некоторой области (D принадлежит R²), и удовлетворяет условию Липинца, то какова бы не была точка (x₀,y₀) (из начального условия) задача Коши имеет единственное решение

3) Теорема пиано: Пусть y^’=f(x,y)

                                      y(x₀)=y₀, если f(x,y) непрерывна в некоторой области D представляющую собой прямоугольник в пространстве R² , то задача коши на отрезке [x₀-h,x₀+h] (где h=const) имеет по крайней мере одно решение

Определение ОДУ с разделяющимися переменными

ОДУ 1-го порядка называется уравнение с разделяющимися переменными, если оно представлено в виде 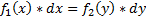 F₁,F₂- некоторые производные), где левая часть содержит только Х, а правая только Y.

Решение ОДУ с разделяющимися переменными

Метод решения: интегрирование обеих частей

Пример:

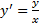 . Найти решение этого ОДУ

. Убедимся, что это ОДУ с раздел. переменными  тогда 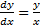, умножим обе части на dx:  делим на y≠0, получим Вывод: ОДУ явл

2. Найдем решение: . Интегрируем обе части: 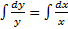получим ln|y|=ln|x|+c (неявно заданная функция, общий интеграл). Это и есть решение.

3. Проверим на наличие частного решения: Делим на y≠0. Кандидат на частное решение: y=0. Проверка: 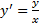; Подставим и получим: 0=0 значит y=0 – частное решение

Ответ: ln|y|=ln|x|+c, y=0

 

Однородные ОДУ 1-го порядка

ОДУ  называется однородным, если выполняется условие f(kx,ky)=f(x,y) где k>0 – произв const

Метод решения: с помощью замены y=U*x,  уравнение сводится к уравнению с разделяющимися переменными.

 

Определение уравнения Лагранжа.

Уравнение Лагранжа

Дифференциальное уравнение вида y=xφ(y′)+ψ(y′)

Решение уравнения Лагранжа.

Полагая y′=p и дифференцируя по переменной x, получаем общее решение уравнения в параметрической форме: {x=f(p,C) y=f(p,C) φ(p)+ψ(p) при условии, что φ(p)−p≠0, где p − параметр.

30. Решение ОДУ 1-го порядка неразрешенных относительно производной. (параметрический метод)

Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид . (1)

Если это уравнение удается разрешить относительно , то получаем одно или несколько уравнений . Интегрируя эти, уже разрешенные относительно производной уравнения, найдем решения исходного уравнения (1).

Теорема ЛОДУ n-го порядка

Формула Абеля

45) три утверждения (теоремы) о формулах частных решениях ЛОДУ n -го порядка 46) общее решение ДЛЖУ 2-го порядка (все случаи, записать формулы)

47) решение ЛОДУ 2-го порядка

          

                                

 

48) правила (формулы) нахождения фундументальной системы решений для ЛОДУ n -го порядка(все случаи) 49) решение ЛОДУ n -го порядка

48)49)

          

50) две теоремы о виде общего решения линейного неоднородного ОДУ n -го порядка (=два метода решения, сформулировать) 51) решения линейного неоднородного ОДУ n -го порядка (любым методом)

50)51)

 

Теорема 4.1

ФСР существуют.

Доказательство.

Рассмотрим систему (4.1) на некотором интервале и зафиксируем . Рассмотрим базис в , состоящий из функций .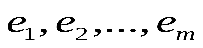

- решение, соответствующее -той задаче Коши.

Определитель Вронского этих решений в т. :

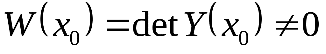(в силу линейной независимости векторов)

Воспользуемся свойством формулы Остроградского-Лиувилля, именно: раз , то .

Для того, чтобы решения были линейно независимыми, необходимо и достаточно, чтобы .

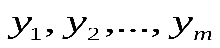- линейно независимы, значит образуют фундаментальную систему решений.

Чтд

Теорема 4.2. Об общем решении однородной системы.

Пусть (4.2) – ФСР системы (4.1).

Тогда любое решение системы (4.1) можно представить в виде линейной комбинации

, (4.4)

где - произвольные константы.

С другой стороны, любая функция вида (4.4) является решением.

Доказательство.

Фиксируем . Пусть - произвольное решение системы (4.1).

Вычислим значения

Они ФСР, значит вектора линейно независимы, следовательно, образуют базис в пространстве . можно разложить по этому базису:

Рассмотрим функцию

с найденными .

, .

Воспользовавшись теоремой единственности, получаем .

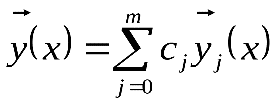справедливо всюду на .

Обратно.

По лемме 2.1 функция (4.4)

Чтд

Рассмотрим систему (4.2)

(4.5)

Теорема 4.3

Если непрерывно-дифференцируемые вектор-функции (4.2) удовлетворяют условию (4.5), то существует система (4.1) с ФСР (4.2).

Доказательство.

То, что (4.2) образует ФСР 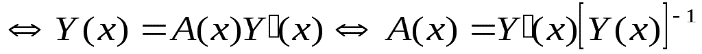. Можем посчитать правую часть. Значит существует и единственна.

Чтд

Замечание 4.1

Вектор-функции (4.2) при удовлетворяют системе

Если разложить этот определитель по I столбцу, то получим систему (4.1)

Решение линейных неоднородных систем ОДУ тремя методами: методом исключения неизвестных; метод вариации постоянных; метод нахождения общего решения как суммы частного решения и решения соответствующей однородной системы ДУ

Определение порядка оду

Наивысший порядок производной в ходящий в оду называется порядком этого уравнения

 

Формы записи оду

1) Оду разрешённые относительно старшей производной

2) Оду не разрешённые относительно старшей производной

3) Оду в диффиринциальной форме (dy=(x²+y²)dx)

 

Определение решиния ОДУ

Решение оду называется функия которая при подстановке в уравнение обращает его в тождество

 

Определение общего, частного решения ОДУ, общего интеграла, интеграла ОДУ

1) Общее решение-если оно представляет собой явно заданную функцию, содержащую произвольные постоянные

2) Частное решение-представляет собой явную функцию, не содержащую произвольные постоянные

3) Общий интеграл представляет собой не явно заданную функцию, содержащую const

4) Интеграл представляет собой не явно заданную функцию, не содержащую произвольные const

 

Определение задачи коши

Задача нахождения решения ОДУ, которая добавляет дополнительное условие называется задачей коши, а дополнительное условие называется начальным