

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...
Топ:
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
1. Интегрирующий множитель зависит от переменной x:μ=μ(x).
В этом случае мы имеем ∂μ∂y=0, поэтому уравнение для μ(x,y) можно записать в виде: 1μdμdx=1Q(∂P∂y−∂Q∂x). Правая часть этого уравнения должна быть только функцией от x. Функцию μ(x) можно найти, интегрируя последнее уравнение.
2. Интегрирующий множитель зависит от переменной y:μ=μ(y).
Аналогично, если ∂μ∂x=0, то мы получаем обыкновенное дифференциальное уравнение, определяющее интегрирующий множитель μ:1μdμdy = −1P(∂P∂y−∂Q∂x), где правая часть зависит только от y. Функция μ(y) находится интегрированием данного уравнения.
3. Интегрирующий множитель зависит от определенной комбинации переменных x и y:μ=μ(z(x,y)).
Новая функция z(x,y) может быть, например, типа: z=xy, z=xy, z=x2+y2, z=x+y, и так далее.
Здесь важно, что интегрирующий множитель μ(x,y) будет являться некоторой функцией одной переменной z:μ(x,y)=μ(z) и может быть найден из дифференциального уравнения: 1μdμdz=∂P∂y−∂Q∂xQ∂z∂x−P∂z∂y.Предполагается, что правая часть уравнения зависит только от z и знаменатель не равен нулю.
26. Определение уравнения Клеро.
Уравнение Клероимеет вид:
y=xy′+ψ(y′)
Уравнение Клеро отличается от уравнения Лагранжа только тем, что в нем коэффициент при 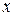 равен
равен 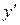
27. Решение уравнения Клеро.

Определение уравнения Лагранжа.
Уравнение Лагранжа
Дифференциальное уравнение вида y=xφ(y′)+ψ(y′)
Решение уравнения Лагранжа.
Полагая y′=p и дифференцируя по переменной x, получаем общее решение уравнения в параметрической форме: {x=f(p,C) y=f(p,C) φ(p)+ψ(p) при условии, что φ(p)−p≠0, где p − параметр.
|
|
30. Решение ОДУ 1-го порядка неразрешенных относительно производной. (параметрический метод)
Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид  . (1)
. (1)
Если это уравнение удается разрешить относительно  , то получаем одно или несколько уравнений
, то получаем одно или несколько уравнений  . Интегрируя эти, уже разрешенные относительно производной уравнения, найдем решения исходного уравнения (1).
. Интегрируя эти, уже разрешенные относительно производной уравнения, найдем решения исходного уравнения (1).
Типы ОДУ 2-го порядка, которые допускают понижение порядка и применение при этом замены переменных.
Среди таких уравнений наиболее часто встречаются ОДУ  , которые не содержат искомой функции и производных до k–1 порядка, и дифференциальные уравнения вида
, которые не содержат искомой функции и производных до k–1 порядка, и дифференциальные уравнения вида  , которые не содержат независимого переменного.
, которые не содержат независимого переменного.
Решение ОДУ 2-го порядка допускающих понижение порядка.
Это дифференциальное уравнение вида 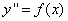 . Произведём замену переменной: введём новую функцию
. Произведём замену переменной: введём новую функцию 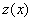 и тогда
и тогда 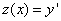 . Следовательно,
. Следовательно, 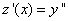 и исходное уравнение превращается в уравнениие первого порядка
и исходное уравнение превращается в уравнениие первого порядка
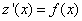
с искомой функцией 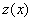 .
.
Решая его, находим 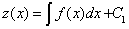 . Так как
. Так как 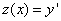 , то
, то 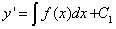 .
.
Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:
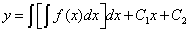 ,
,
где 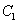 и
и 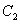 - произвольные константы интегрирования.
- произвольные константы интегрирования.
Решение ОДУ 2-го порядка, допускающих понижение порядка
Общий вид F(x, y, y’, y’’)= 0 или y’’= f(x, y, y’). Общее решение y = g(x, C1,C2) содержит две произвольные константы и обращает ДУ в верное тождество.
|
|
|

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!