

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
Топ:
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В общем виде систему из n дифференциальных уравнений 1-го порядка можно записать следующим образом: 

где  – неизвестные функции независимой переменной t,
– неизвестные функции независимой переменной t, 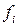 – некоторые заданные функции. Общее решение системы (2.1) содержит n произвольных констант, т.е. имеет вид:
– некоторые заданные функции. Общее решение системы (2.1) содержит n произвольных констант, т.е. имеет вид:

При описании реальных задач с помощью систем дифференциальных уравнений конкретное решение, или частное решение системы находится из общего решения заданием некоторых начальных условий. Начальное условие записывается для каждой функции  и для системы n уравнений 1-го порядка выглядит так:
и для системы n уравнений 1-го порядка выглядит так:

Решения  определяют в пространстве
определяют в пространстве  линию, которая называется интегральной линией системы (2.1).
линию, которая называется интегральной линией системы (2.1).
Сформулируем теорему существования и единственности решения для систем дифференциальных уравнений.
Теорема Коши. Система дифференциальных уравнений 1-го порядка (2.1) вместе с начальными условиями (2.2) имеет единственное решение (т.е. из общего решения определяется единственный набор констант 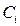 ), если функции
), если функции 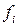 и их частные производные по всем аргументам
и их частные производные по всем аргументам  ограничены в окрестности этих начальных условий.
ограничены в окрестности этих начальных условий.
Естественно речь идет о решении в какой-то области  переменных
переменных  .
.
Решение системы дифференциальных уравнений  можно рассматривать как вектор-функцию X, компонентами которого являются функции
можно рассматривать как вектор-функцию X, компонентами которого являются функции  а набор функций
а набор функций 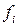 – как вектор-функцию F, т.е.
– как вектор-функцию F, т.е.

Используя такие обозначения, можно кратко переписать исходную систему (2.1) и начальные условия (2.2) в так называемой векторной форме:
 (2.1a)
(2.1a)
 (2.2a)
(2.2a)
Одним из методов решения системы дифференциальных уравнений является сведение этой системы к одному уравнению более высокого порядка. Из уравнений (2.1), а также уравнений, полученных их дифференцированием, можно получить одно уравнение n -го порядка для любой из неизвестных функций  Интегрируя его, находят неизвестную функцию
Интегрируя его, находят неизвестную функцию  Остальные неизвестные функции получаются из уравнений исходной системы и промежуточных уравнений, полученных при дифференцировании исходных
Остальные неизвестные функции получаются из уравнений исходной системы и промежуточных уравнений, полученных при дифференцировании исходных
|
|
53) определение разрешенной системы ОДУ 
60. Утверждение (теорема) об общем решении ЛОСДУ (связь с фундаментальной системой решений)
 (4.1)
(4.1)
 (4.2)
(4.2)
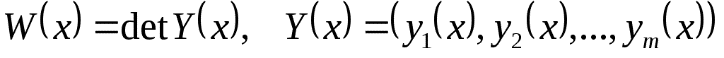 (4.3)
(4.3)
Определение.
Система из  линейно независимых вектор-функций (4.2), которые являются решениями системы (4.1), называется фундаментальной системой решений системы (4.1). Тогда матрица (4.3), составленная из системы ФСР, называется фундаментальной матрицей.
линейно независимых вектор-функций (4.2), которые являются решениями системы (4.1), называется фундаментальной системой решений системы (4.1). Тогда матрица (4.3), составленная из системы ФСР, называется фундаментальной матрицей.
Теорема 4.1
ФСР существуют.
Доказательство.
Рассмотрим систему (4.1) на некотором интервале  и зафиксируем
и зафиксируем  . Рассмотрим базис в
. Рассмотрим базис в  , состоящий из функций
, состоящий из функций 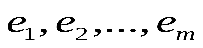 .
.

 - решение, соответствующее
- решение, соответствующее  -той задаче Коши.
-той задаче Коши.
Определитель Вронского этих решений в т.  :
:
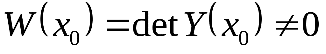 (в силу линейной независимости векторов)
(в силу линейной независимости векторов)
Воспользуемся свойством формулы Остроградского-Лиувилля, именно: раз  , то
, то  .
.
Для того, чтобы решения были линейно независимыми, необходимо и достаточно, чтобы  .
.
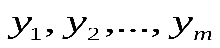 - линейно независимы, значит образуют фундаментальную систему решений.
- линейно независимы, значит образуют фундаментальную систему решений.
Чтд
Теорема 4.2. Об общем решении однородной системы.
Пусть (4.2) – ФСР системы (4.1).
Тогда любое решение  системы (4.1) можно представить в виде линейной комбинации
системы (4.1) можно представить в виде линейной комбинации
 , (4.4)
, (4.4)
где  - произвольные константы.
- произвольные константы.
С другой стороны, любая функция вида (4.4) является решением.
Доказательство.
Фиксируем  . Пусть
. Пусть  - произвольное решение системы (4.1).
- произвольное решение системы (4.1).
Вычислим значения

Они ФСР, значит вектора линейно независимы, следовательно, образуют базис в пространстве  .
.  можно разложить по этому базису:
можно разложить по этому базису:

Рассмотрим функцию
 с найденными
с найденными  .
.
 ,
,  .
.
Воспользовавшись теоремой единственности, получаем  .
.
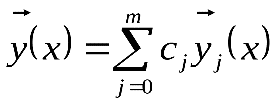 справедливо всюду на
справедливо всюду на  .
.
Обратно.
По лемме 2.1 функция (4.4)
Чтд
Рассмотрим систему (4.2)

 (4.5)
(4.5)
Теорема 4.3
Если непрерывно-дифференцируемые вектор-функции (4.2) удовлетворяют условию (4.5), то существует система (4.1) с ФСР (4.2).
|
|
Доказательство.
То, что (4.2) образует ФСР 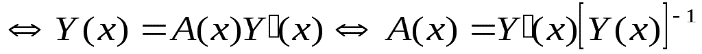 . Можем посчитать правую часть. Значит
. Можем посчитать правую часть. Значит  существует и единственна.
существует и единственна.
Чтд
Замечание 4.1
Вектор-функции (4.2)  при
при  удовлетворяют системе
удовлетворяют системе

Если разложить этот определитель по I столбцу, то получим систему (4.1)
|
|
|

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!