

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Определение. Функциональным рядом называется выражение:
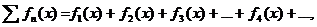 ,
,
члены которого 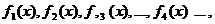 являются функциями от
являются функциями от  .
.
Придавая  числовое значение
числовое значение 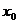 , мы получаем числовой ряд
, мы получаем числовой ряд
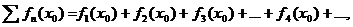
который может быть как сходящимся, так и расходящимся.
Определение. Множество тех значений  , при которых функциональный ряд сходится, называется его областью сходимости.
, при которых функциональный ряд сходится, называется его областью сходимости.
Ясно, что в области сходимости сумма функционального ряда является некоторой функцией от  . Обозначим се через
. Обозначим се через  .
.
Функциональный ряд сходится в точке x0, если сходится числовой ряд.
Функциональный ряд сходится на интервале J, если он сходится в каждой точке этого интервала.
Специальный класс функциональных рядов составляют так называемые степенные ряды вида
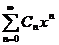 =
= 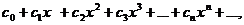 ,
,
где 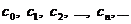 -последовательность действительных чисел, называют коэффициентами ряда.
-последовательность действительных чисел, называют коэффициентами ряда.
Выясним, какой вид имеет «область сходимости» степенного ряда, тоесть множество 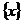 тех значений переменной, для которых ряд сходится.
тех значений переменной, для которых ряд сходится.
Теорема Абеля. Если степенной ряд 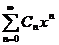 сходится в точке
сходится в точке 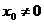 , то он сходится и притом абсолютно в интервале
, то он сходится и притом абсолютно в интервале 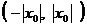 , то есть при всех значениях
, то есть при всех значениях  , удовлетворяющих условию.
, удовлетворяющих условию. 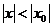 .
.
Следствие. Если степенной ряд расходится при некотором значении 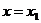 , то он расходится и при всех значениях
, то он расходится и при всех значениях 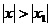 .
.
Любой степенной ряд сходится при значении 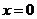 . Естьстепенныеряды, которые сходятся только при
. Естьстепенныеряды, которые сходятся только при 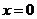 и расходятся приостальныхзначениях
и расходятся приостальныхзначениях  .
.
Область сходимости может состоять из всех точекоси Ох, другимисловами, ряд может сходится при всех  .
.
Пример. Исследовать сходимость ряда 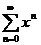 .
.
Решение:
Ряд 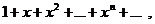 представляет геометрическую прогрессию со знаменателем
представляет геометрическую прогрессию со знаменателем  , сходится при
, сходится при  и расходитсяпри
и расходитсяпри 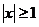 .
.
Из теоремы Абеля и ее следствия получаем, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости. Совершенно ясно, что точки сходимости будут целиком заполнять некоторый интервал с центром в начале координат.
|
|
Таким образом, можно сказать, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число  , что для всех
, что для всех  , по модулю меньших
, по модулю меньших 
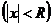 , ряд абсолютно сходится, а для всех
, ряд абсолютно сходится, а для всех  , по модулю больших
, по модулю больших 
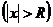 , ряд расходится.
, ряд расходится.
Что касается значений  здесь могут быть различные возможности: ряд может сходится в обеих точках, или только в одной из них, или ни в одной. При этом ряд может сходиться как абсолютно, так и условно.
здесь могут быть различные возможности: ряд может сходится в обеих точках, или только в одной из них, или ни в одной. При этом ряд может сходиться как абсолютно, так и условно.
Определение. Радиусом сходимостистепенного ряда 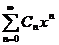 называетсятакое число
называетсятакое число  , что для всех
, что для всех  ,
, 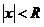 , степенной ряд сходится, а для всех
, степенной ряд сходится, а для всех 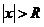 , расходится. Интервал
, расходится. Интервал 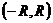 называется интервалом сходимости.
называется интервалом сходимости.
Условимся для рядов, расходящихся при всех  , кроме
, кроме 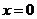 . считать
. считать 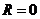 , а для рядов, сходящихся при всех
, а для рядов, сходящихся при всех  , считать
, считать 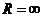 .
.
Как найти радиус сходимости?
Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при 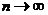 отношения абсолютных величин коэффициентов общего и следующего за ним членов ряда.
отношения абсолютных величин коэффициентов общего и следующего за ним членов ряда.
Составим ряд из абсолютных величин членов ряда 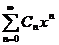
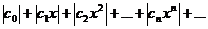
Найдем отношение 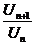 для этого ряда:
для этого ряда:

а затем предел его при 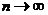 :
:
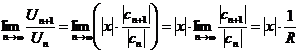
Здесь множитель 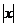 вынесен за знак предела, как не зависящий от
вынесен за знак предела, как не зависящий от 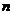 и введено обозначение
и введено обозначение
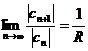 ,
,
если этот предел существует и не равен нулю. Согласно признаку Даламбера, ряд сходится, если  ,. откуда
,. откуда 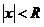 . Отсюда следует, что ряд сходится, и притом абсолютно, при значениях
. Отсюда следует, что ряд сходится, и притом абсолютно, при значениях 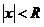 .
.
Согласно томуже признаку Даламбера, ряд расходится, если 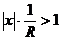 или
или 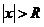 . Однако в этом случае из признака Даламбера следует, что члены ряда не стремятся к нулю. Тогда при
. Однако в этом случае из признака Даламбера следует, что члены ряда не стремятся к нулю. Тогда при 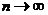 не стремятся к нулю и члены ряда, а потому и он расходится при значениях
не стремятся к нулю и члены ряда, а потому и он расходится при значениях 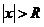 . Следовательно, согласно определению, число
. Следовательно, согласно определению, число  – радиус сходимости степенного ряда. из соотношения получим
– радиус сходимости степенного ряда. из соотношения получим
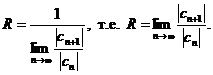
Пример. Найти радиус сходимости рядов:
а). 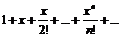 б).
б). 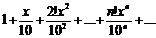 в).
в). 
Решение:
а). 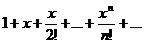

б). 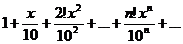
|
|
Найдем отношение
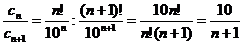
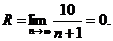 т. е. ряд сходится только при
т. е. ряд сходится только при 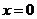 и расходится при остальных значениях
и расходится при остальных значениях  .
.
в). 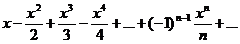
Здесь 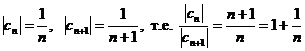
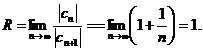
Исследуем сходимость ряда на концах интервала сходимости.
При 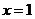 имеем ряд
имеем ряд 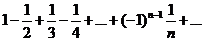 он сходится по теореме Лейбница.
он сходится по теореме Лейбница.
При 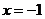 имеем ряд
имеем ряд  , который расходится как произведение расходящегося гармонического ряда на -1. Следовательно; областью сходимости служит полуинтервал
, который расходится как произведение расходящегося гармонического ряда на -1. Следовательно; областью сходимости служит полуинтервал 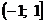 .
.
Пример. Найти область сходимости степенного ряда
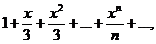
Решение:
Найдем радиус сходимости ряда
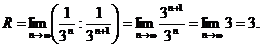
Исследуем сходимость ряда при значениях 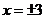 . Подставив их в данный ряд соответственно получим
. Подставив их в данный ряд соответственно получим 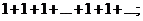
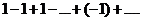 Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при
Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при 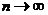 ). На обоих концах интервала сходимости данный ряд расходится а область его сходимости
). На обоих концах интервала сходимости данный ряд расходится а область его сходимости 
Замечание. Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда начиная с некоторого, отличны от нуля. Применение формулы допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать или с помощью признаков Даламбера. Коши, или же сделав замену переменной, преобразованием ряда к виду в котором указанное условие выполняется.
Свойства степенных рядов
Рассмотрим степенной ряд  имеющий радиус сходимости
имеющий радиус сходимости 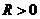 (
( может равняться
может равняться  ). Тогда каждому значению
). Тогда каждому значению  из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от
из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от  на интервале сходимости. Обозначим ее через
на интервале сходимости. Обозначим ее через  . Тогда можно записать равенство
. Тогда можно записать равенство  понимая его в том смысле, что сумма ряда в каждой точке
понимая его в том смысле, что сумма ряда в каждой точке  из интервала сходимости равна значению функции
из интервала сходимости равна значению функции  в этой точке. В этом же смысле будем говорить, что ряд сходится к функции
в этой точке. В этом же смысле будем говорить, что ряд сходится к функции  на интервале сходимости. Вне интервала сходимости равенство не имеет смысла.
на интервале сходимости. Вне интервала сходимости равенство не имеет смысла.
Для степенных рядов справедливы следующие утверждения:
1) Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд а суммы их соответственно равны  .
.
2) Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до  , если
, если  , причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
|
|

|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!