

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
Топ:
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
Понятие определенного интеграла и его свойства
Пусть на отрезке  задана функция y=f(x). Разобьем отрезок
задана функция y=f(x). Разобьем отрезок  на n элементарных отрезков точками
на n элементарных отрезков точками  . На каждом отрезке
. На каждом отрезке  разбиения выберем некоторую точку
разбиения выберем некоторую точку  и положим
и положим  , где
, где  . Сумму вида
. Сумму вида
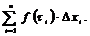
будем называть интегральной суммой для функции y=f(x) на  . Очевидно, что интегральная сумма зависит как от способа разбиения отрезка
. Очевидно, что интегральная сумма зависит как от способа разбиения отрезка  точками
точками  , так и от выбора точек
, так и от выбора точек  на каждом из отрезков разбиения
на каждом из отрезков разбиения  ,
,  .
.
 |
Если существует предел  , не зависящий от способа разбиения отрезка
, не зависящий от способа разбиения отрезка  и выбора точек
и выбора точек  , то этот предел будем называть определённым интегралом функции f(x) на отрезке
, то этот предел будем называть определённым интегралом функции f(x) на отрезке  и обозначать символом
и обозначать символом  т.е.
т.е.

Функция f(x) в этом случае называется интегрируемой на отрезке  . При этом f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, а числа a и b – пределами интегрирования (a – нижний предел, b – верхний предел), а сумма
. При этом f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, а числа a и b – пределами интегрирования (a – нижний предел, b – верхний предел), а сумма  – интегральной суммой.
– интегральной суммой.
Теорема. Если функция f(x) непрерывна на отрезке  , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
Свойства определённого интеграла
1. 
2. Постоянный множитель можно выносить за знак определённого интеграла:

3. Определённый интеграл от суммы двух функций равен сумме определённых интегралов от этих функций:

4. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный:

5. Интеграл по отрезку равен сумме интегралов по его частям:
 где a<c<b.
где a<c<b.
Формула Ньютона-Лейбница
Если функция f(x) непрерывна на отрезке  и F(x) – первообразная функции f(x) на этом отрезке, то:
и F(x) – первообразная функции f(x) на этом отрезке, то:

Эта формула называется формулой Ньютона-Лейбница.
При вычислении интегралов ее часто записывают в виде

Пример.
 =
= 
Геометрические приложения определённого интеграла
Вычисления площадей плоских фигур
 Пусть функция f(x) непрерывна на отрезке
Пусть функция f(x) непрерывна на отрезке  . Если при этом f(x)
. Если при этом f(x)  на этом отрезке, то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла:
на этом отрезке, то площадь S криволинейной трапеции, ограниченной линиями y=f(x), y=0, x=a, x=b, выразится с помощью интеграла: 
Замечания.
 1. Если же
1. Если же  на
на  , то – f(х)
, то – f(х)  на этом отрезке. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле:
на этом отрезке. Поэтому площадь S соответствующей криволинейной трапеции находится по формуле:

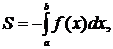 или
или 
Наконец, если линия y=f(x) пересекает ось Ох, то отрезок  надо разбить на части, в пределах которых f(x) не меняет знака, и к каждой части применить ту из формул, которая ей соответствует.
надо разбить на части, в пределах которых f(x) не меняет знака, и к каждой части применить ту из формул, которая ей соответствует.
 2. Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу – графиком функции y1=f1(x), слева и справа прямыми x=a, x=b, вычисляется по формуле:
2. Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу – графиком функции y1=f1(x), слева и справа прямыми x=a, x=b, вычисляется по формуле: 


 3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=j2(y), слева – графиком функции x1=j1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле:
3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=j2(y), слева – графиком функции x1=j1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле: 
Пример. Найти площадь плоской фигуры, ограниченной графиком функции y = sin x и осью абсцисс при условии  .
.
Решение:
Разобьём отрезок  на два отрезка:
на два отрезка:  и
и  . На первом из них sin x
. На первом из них sin x  , на втором sin x
, на втором sin x 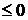 . Тогда, используя формулы, находим искомую площадь:
. Тогда, используя формулы, находим искомую площадь:
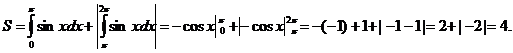

Примеры решения типовых задач
№1. Вычислить площадь фигуры, ограниченной линиями  и
и 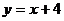 .
.
Решение:
1. Найдем пределы интегрирования, в качестве  и
и 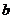 возьмем абсциссы точек пересечения данных линий.
возьмем абсциссы точек пересечения данных линий.
Для их нахождения решим систему уравнений:


 ;
;
 ;
;
 ,
, 
 2. Определим, какой график расположен выше. Для этого построим заданные линии. Графиком функции
2. Определим, какой график расположен выше. Для этого построим заданные линии. Графиком функции  является парабола. Найдем координаты вершины параболы:
является парабола. Найдем координаты вершины параболы:
 ,
,  .
.
Найдем точку пересечения параболы с осями координат:
 ,
, 
 ,
, 
 и
и  .
.
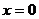 ,
, 
 .
.
Получили две точки пересечения с осью  :
:  и
и  .
.
Графиком функции 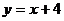 является прямая линия, для построения которой достаточно взять две точки.
является прямая линия, для построения которой достаточно взять две точки.
Из рисунка видно, что график функции 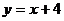 находится выше графика функции
находится выше графика функции  , следовательно, выполняется условие
, следовательно, выполняется условие  .
.
Применяя формулу (2), найдем площадь фигуры, ограниченной заданными линиями:
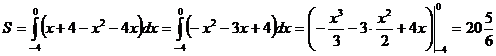 (кв.ед.)
(кв.ед.)
№2. Вычислить объем тела, полученного вращением вокруг оси  криволинейной трапеции, ограниченной гиперболой
криволинейной трапеции, ограниченной гиперболой  , прямыми
, прямыми 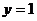 ,
,  и осью Оу.
и осью Оу.
Решение:  ,
,  ,
,  . Тогда
. Тогда  .
.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!