ВВЕДЕНИЕ
Самостоятельная работа студентов играет большую роль в системе высшего образования. Она включает изучение теоретического материала, применение различных подходов и приемов к решению типовых задач по каждой теме, самостоятельное выполнение индивидуальных заданий. Данные методическое указания содержат необходимый минимум программы курса высшей математики, достаточный для усвоения специальных дисциплин экономического профиля, преподаваемых в сельскохозяйственных вузах. Наличие решенных типовых примеров в случае необходимости поможет правильно выбрать метод решения той или иной задачи.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. К у д р я в ц е в, В. А. Краткий курс высшей математики / В. А. Кудрявцев,
В.П. Демидович –.М.: Наука, 1985.
2. Л о б о ц к а я, Н. Л. Основы высшей математики / Н. Л. Лобоцкая. –Минск: Вышэйш. шк., 1978.
3. М и н о р с к и й, В. П. Сборник задач по высшей математике / В. П. Минорский.–М.: Наука, 1987.
4. К л е т е н и к, Д. В. Сборник задач по аналитической геометрии / Д. В. Клетеник. –М.: Наука, 1986.
5. Высшая математика. Общий курс / под ред. проф. А. И.Яблонского. –Минск: Вышэйш. шк., 1993.
6. Г у с а к, А. А. Высшая математика /А. А. Гусак. – Минск, 2000. –Т.1.
7. Г у с а к, А. А. Высшая математика / А. А. Гусак.– Минск, 2000. –Т.2.
8. Л и х о л е т о в, И. И. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике / И. И. Лихолетов, И. П. Мацкевич.– Минск: Вышэйш. шк., 1976.
9. Б у л д ы к, Г. М. Теория вероятностей и математическая статистика/ Г. М.Булдык. –Минск: Вышэйш. шк., 1989.
10. М а ц к е в и ч, И. П. Теория вероятностей и математическая статистика/ И. П. Мацкевич., Г. П. Свирид. –Минск: Вышэйш. шк., 1993.
11. Г у р с к и й, Е. И. Сборник задач по теории вероятностей и математической статистике / Е. И. Гурский. –Минск: Вышэйш. шк., 1984.
12. М а ц к е в и ч, И. П. Сборник задач и упражнений. Теория вероятностей и математическая статистика / И. П. Мацкевич, Г. П. Свирид, Г. М. Булдык.– Минск: Вышэйш. шк., 1996.
Т е м а 1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Изучение этой темы следует начать с теории определителей как удобного инструмента при решении систем линейных уравнений, задач векторной алгебры и аналитической геометрии на плоскости и в пространстве. Далее необходимо разобраться в методе координат, ознакомиться с системами координат на прямой, плоскости и в пространстве. Особое внимание следует уделить понятию уравнения линии на плоскости, уравнениям линии и поверхности в пространстве. Решение задач аналитической геометрии требует знания различных видов уравнений прямой линии на плоскости и в пространстве, уравнений плоскости, определений и канонических уравнений кривых и поверхностей второго порядка. Использование понятия и свойств вектора, а также умение производить действия над векторами является необходимым условием достижения цели. Перед выполнением контрольной работы следует изучить соответствующие разделы рекомендуемой литературы.
ВОПРОСЫ ДЛЯ ИЗУЧЕНИЯ И САМОПРОВЕРКИ
1. Определитель и его свойства.
2. Способы вычисления определителей.
3. Формулы Крамера.
4. Системы координат.
5. Векторы. Линейные операции над векторами.
6. Скалярное, векторное и смешанное произведения векторов и их свойства. Применение скалярного, векторного и смешанного произведения векторов.
7. Расстояние между двумя точками.
8. Деление отрезка в заданном отношении.
9. Виды уравнений прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.
10.Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямой и плоскостью. Расстояние от точки до плоскости.
11.Кривые и поверхности второго порядка, их геометрические свойства.
Задачи 1–20. Даны координаты точек А,В,С,D. Найти:
1) модули векторов 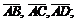
2) разложение вектора  по базису
по базису 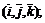
3) проекцию вектора  на вектор
на вектор  ;
;
4) внутренний угол А треугольника АВС;
5) проверить коллинеарность и перпендикулярность векторов
 и
и 
1. А(3;4;5); В(-1;2;3); С(4;-1;0); D(2;1;-2).
2. А(-2;-3;2); В(-1;-5;4); С(9;-1;12); D(6;1;10).
3. А(2;-1;4); В(3;-3;-2); С(13;1;6); D(10;3;4).
4. А(-8;3;-1); В(-7;1;1); С(3;5;9); D(0;7;7).
5. А(3;1;-2); В(4;-1;0); С(14;3;8); D(11;5;6).
6. А(0;2;-10); В(1;0;-8); С(11;4;0); D(8;6;-2).
7. А(-1;-2;-8); В(0;-4;-6); С(10;0;2); D(7;2;0).
8. А(1;-4;0); В(2;-6;2); С(12;-2;10); D(9;0;8).
9. А(-5;0;1); В(-4;-2;3); С(6;2;11); D(3;4;9).
10. А(4;-2;5); В(8;2;3); С(6;9;-5); D(4;0;6).
11. А(3;3;-4); В(7;7;-5); С(5;14;-13) D(3;5;-2).
12. А(-2;0;-2); В(2;4;-4); С(0;11;-12); D(-2;2;-1).
13. А(0;4;3); В(4;8;1); С(2;15;7); D(0;6;4).
14. А(-4;2;-1); В(0;6;-3); С(-2;13;-11); D(-4;4;0).
15. А(-1;1;-5); В(3;5;-7); С(1;12;-15); D(-1;3;-4).
16. А(-3;-6;2); В(1;-2;0); С(-1;5;-8); D(-3;-4;3).
17. А(1;-4;0); В(5;0;-2); С(3;7;-10); D(1;-2;1).
18. А(5;-1;-4); В(9;3;-6); С(7;10;-14); D(5;1;-3).
19. А(2;-3;1); В(6;1;-1); С(4;8;-9); D(2;-1;2).
20. А(-4;5;-5); В(-3;3;-3); С(7;7;5); D(4;9;3).
Решение типового примера
Пусть координаты точек: А(-3;4;-3); В(-2;2;1); С(8;6;7); D(5;8;5).
1.Произвольный вектор  может быть разложен по базису
может быть разложен по базису 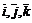 следующим образом:
следующим образом:  , где
, где  – проекции вектора
– проекции вектора  на координатные оси ОХ,ОУ,ОZ, a
на координатные оси ОХ,ОУ,ОZ, a 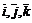 –единичные векторы, направления которых совпадают с направлением осей ОХ,ОУ,ОZ.
–единичные векторы, направления которых совпадают с направлением осей ОХ,ОУ,ОZ.
Проекции вектора на оси находим следующим образом: из координат конца вектора вычитаем координаты начала вектора. Следовательно, координаты вектора 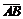 (–2+3; 2–4; –1+3);
(–2+3; 2–4; –1+3); 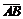 (1;–2;2), 2
(1;–2;2), 2 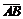 (2;–4;4). Координаты вектора
(2;–4;4). Координаты вектора  (–3–8; 4–6; –3–7);
(–3–8; 4–6; –3–7);
 (–11;–2;–10); 3
(–11;–2;–10); 3  (–33;–6;–30); 2
(–33;–6;–30); 2 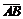 +3
+3  (2–33;–4–6;4–30);
(2–33;–4–6;4–30);
2 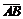 +3
+3  (–31;–10;–26); 2
(–31;–10;–26); 2 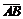 +3
+3  =–31
=–31  –10
–10 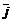 –26
–26 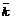 .
.
2. Модуль вектора вычисляется по формуле: 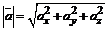 .
.
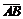 (1;–2;2);
(1;–2;2);  (11;2;10);
(11;2;10);  (8:4;8). Тогда
(8:4;8). Тогда  =3;
=3;  =15;
=15;  =12.
=12.
3. Проекция вектора (2 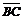 –
– 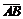 ) на вектор
) на вектор  равна скалярному произведению этих векторов, деленному на модуль вектора
равна скалярному произведению этих векторов, деленному на модуль вектора  .
. 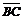 (10;4;8); 2
(10;4;8); 2 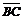 (20;8;16); 2
(20;8;16); 2 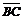 –
– 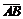 (19;10;14);
(19;10;14);

 =
=  .
.
4. Для того, чтобы найти косинус угла между векторами, нужно скалярное произведение этих векторов поделить на произведение их модулей.
Угол А – это угол между векторами  и
и  .
.


 .
.
5. Условие коллинеарности векторов: соответствующие координаты должны быть пропорциональны.
2  +3
+3  (–31;–10;–26); 2
(–31;–10;–26); 2 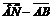 (19;10;14);
(19;10;14);
 .
.
Значит данные векторы не коллинеарны.
Условие перпендикулярности двух векторов: их скалярное произведение должно быть равно нулю.
 =31∙ 19-10∙ 10-26 ∙14≠0, следовательно, данные векторы не перпендикулярны.
=31∙ 19-10∙ 10-26 ∙14≠0, следовательно, данные векторы не перпендикулярны.
Функции одной переменной
Для успешного усвоения этой темы необходимо разобраться в фундаментальном понятии математического анализа – понятии функции, изучить способы задания функции, свойства основных элементарных функций. При исследовании и анализе поведения функций не обойтись без понятий предела функции, бесконечно малой величины, ограниченной и непрерывной функций. Теоремы о пределах, замечательные пределы играют особую роль при решении задач по этой теме.
ВОПРОСЫ ДЛЯ ИЗУЧЕНИЯ И САМОПРОВЕРКИ
1. Множество действительных чисел. Функция, бластьопределения функции, способы задания функции.
2. Основные элементарные функции, их свойства и графики.
3. Сложные и обратные функции, их графики.
4. Предел функции в точке и на бесконечности. Теоремы о преде-лах. Замечательные пределы.
5. Пределы монотонных функций.
6. Непрерывность функций в точке, на интервале.
7. Непрерывность основных элементарных функций.
8. Бесконечно малые и бесконечно большие функции, их свойства. Сравнение бесконечно малых.
9. Свойства непрерывных на отрезке функций.
Задачи 61–80. Найти пределы заданных функций.
61. а) 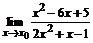 , ,
|
при 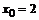 , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
62. а)  , ,
|
при  , , 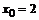 , ,  ; ;
|
б)  ; ;
| в)  . .
|
63. а)  , ,
|
при 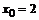 , ,  , ,  ; ;
|
б)  ; ;
| в) 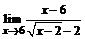 . .
|
64. а)  , ,
|
при 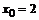 , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
65. а) 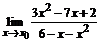 , ,
|
при  , , 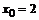 , ,  ; ;
|
б)  ; ;
| в)  . .
|
66. а)  , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
67. а)  , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
|
в)  . .
|
68. а)  , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
69. а)  , ,
|
при  , , 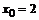 , ,  ; ;
|
б) 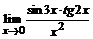 ; ;
| в)  . .
|
70. а) 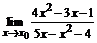 , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
71. а)  , ,
|
при 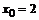 , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
72. а)  , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
73. а)  , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
| в) 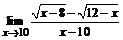 . .
|
74. а)  , ,
|
при 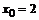 , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
75. а)  , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
76. а)  , ,
|
при  , , 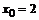 , ,  ; ;
|
б)  ; ;
| в)  . .
|
77. а)  , ,
|
при 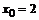 , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
78. a) 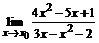 , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
79. a)  , ,
|
при  , ,  , ,  ; ;
|
б)  ; ;
| в)  . .
|
80. а) 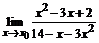 , ,
|
при  , , 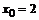 , ,  ; ;
|
б)  ; ;
|
в)  . .
|
Решение типовых примеров
П р и м е р ы. Найти указанные пределы:
1.  .
.
2.  .
.
При подстановке предельного значения х=-1 получим неопределенность вида  . Для раскрытия неопределенности в данном случае разложим числитель и знаменатель дроби на линейные множители по формуле:
. Для раскрытия неопределенности в данном случае разложим числитель и знаменатель дроби на линейные множители по формуле:  , где х1 и х2 –корни квадратного трехчлена
, где х1 и х2 –корни квадратного трехчлена  .
.
 .
.
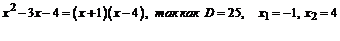 .
.
Следовательно: 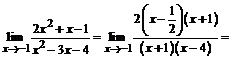
 .
.
3.  Для раскрытия неопределенности
Для раскрытия неопределенности 
разделим числитель и знаменатель дроби на переменную в старшей степени, т.е. на х2:
 .
.
4.  . В данном случае неопределенность вида
. В данном случае неопределенность вида  раскрываем с использованием первого замечательного предела и его следствия:
раскрываем с использованием первого замечательного предела и его следствия:  ;
;  .
.
 .
.
5.  . Для раскрытия данного вида неопределенности нужно домножить числитель и знаменатель дроби на выражение, сопряженное числителю:
. Для раскрытия данного вида неопределенности нужно домножить числитель и знаменатель дроби на выражение, сопряженное числителю:

= 

 .
.
Необходимо знать формулу:  .
.
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Вопросы программы для изучения и самопроверки
1. Производная функции, ее геометрический смысл.
2. Правила дифференцирования функций.
3. Производная сложной, неявно заданной и обратной функций.
4. Дифференцирование функций, заданных параметрически.
5. Дифференциал функции.
6. Производные и дифференциалы высших порядков.
7. Теоремы Ролля, Лагранжа, Коши. Правило Лопиталя.
8. Условия возрастания и убывания функций. Экстремум функции. Необходимое условие экстремума. Достаточные признаки существо- вания экстремума.
9. Наибольшее и наименьшее значения непрерывной на отрезке функции.
10. Выпуклость и вогнутость графика функции. Точки перегиба.
11. Асимптоты кривых.
Задачи 81–100. Найти производные заданных функций.
81. а) 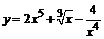 ; ;
| б) 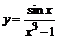 ; ;
|
в) 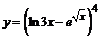 . .
|
|
82. а) 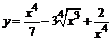 ; ;
| б) 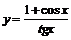 ; ;
|
в) 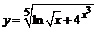 . .
|
|
83. а) 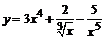 ; ;
| б) 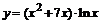 ; ;
|
в) 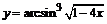 . .
|
|
84. а) 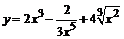 ; ;
| б) 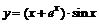 ; ;
|
в) 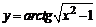 . .
|
|
85. а) 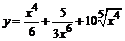 ; ;
| б) 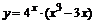 ; ;
|
в) 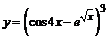 . .
|
|
86. а) 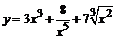 ; ;
| б)  ; ;
|
в) 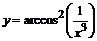 . .
|
|
87. а) 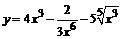 ; ;
| б) 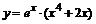 ; ;
|
в) 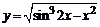 . .
|
|
88. а) 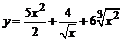 ; ;
| б) 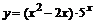 ; ;
|
в) 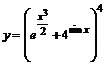 . .
|
|
89. а) 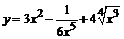 ; ;
| б) 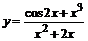 ; ;
|
в) 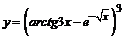 . .
|
|
90. а) 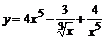 ; ;
| б) 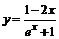 ; ;
|
в) 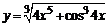 . .
|
|
91. а) 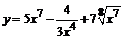 ; ;
| б) 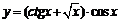 ; ;
|
в) 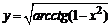 . .
|
|
92. а) 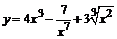 ; ;
| б) 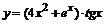 ; ;
|
в) 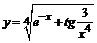 . .
|
|
93. а) 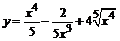 ; ;
| б) 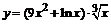 ; ;
|
в) 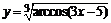 . .
|
|
94. а) 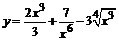 ; ;
| б) 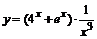 ; ;
|
в) 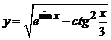 . .
|
|
95. а) 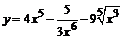 ; ;
| б)  ; ;
|
в) 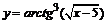 . .
|
|
96. а) 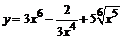 ; ;
| б) 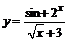 ; ;
|
в) 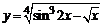 . .
|
|
97. а) 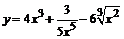 ; ;
| б) 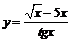 ; ;
|
в) 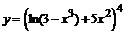 . .
|
|
98. а) 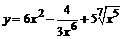 ; ;
| б)  ; ;
|
в) 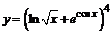 . .
|
|
99. а) 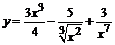 ; ;
| б) 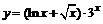 ; ;
|
в) 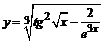 . .
|
|
100. а) 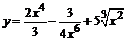 ; ;
| б) 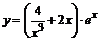 ; ;
|
в) 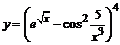 . .
|
|
Решение типовых примеров
При решении примеров рекомендуется использовать правила дифференцирования и таблицу производных.
Таблица производных
|
1.
|
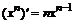
|
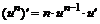
|
| 2.
| 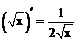
| 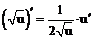
|
| 3.
| 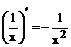
|  
|
| 4.
| 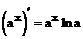
| 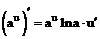
|
| 5.
| 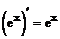
| 
|
| 6.
| 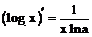
| 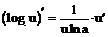
|
| 7.
| 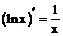
| 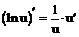
|
| 8.
| 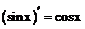
| 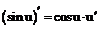
|
| 9.
| 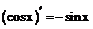
| 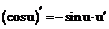
|
| 10.
| 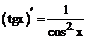
| 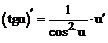
|
| 11.
| 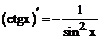
| 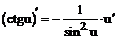
|
| 12.
| 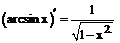
| 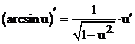
|
| 13.
| 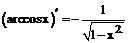
| 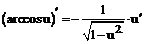
|
| 14.
| 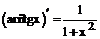
| 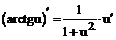
|
| 15.
| 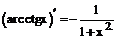
| 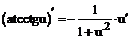
|
Правила дифференцирования
Если С – постоянная величина и функции 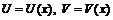 имеют производные, то:
имеют производные, то:
1. 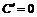 .
.
2. а) 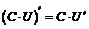 .
.
б) 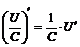 .
.
3. 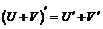 .
.
4. 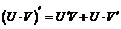 .
.
5. 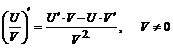
6. Производная сложной функции 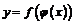 вычисляется по формуле
вычисляется по формуле 
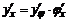 .
.
П р и м е р ы. Найти производные заданных функций:
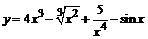 .
.
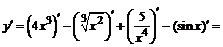
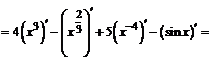
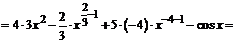
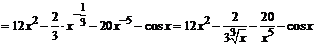 ;
;
2. 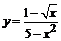 .
.
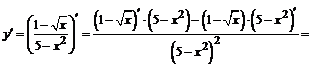
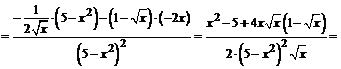
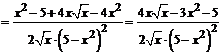 .
.
3. 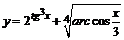 .
.
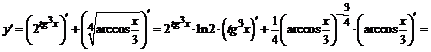
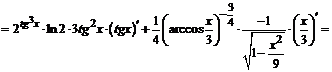
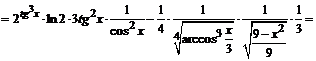
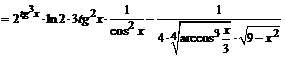 .
.
Задача 101–120. Провести полное исследование заданных функций и построить их графики.
101. 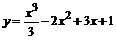 . .
| 102. 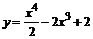 . .
|
103. 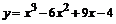 . .
| 104. 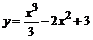 . .
|
105. 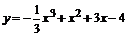 . .
| 106. 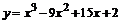 . .
|
107. 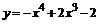 . .
| 108. 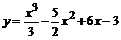 . .
|
109. 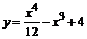 . .
| 110. 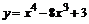 . .
|
111. 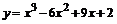 . .
| 112. 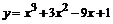 . .
|
113. 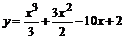 . .
| 114. 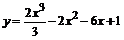 . .
|
115. 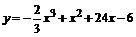 . .
| 116. 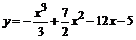 . .
|
117. 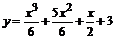 . .
| 118. 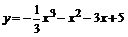 . .
|
119. 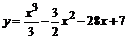 . .
| 120. 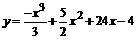 . .
|
Решение типового примера
П р и м е р. Исследовать функцию 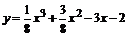 и пост -роить ее график.
и пост -роить ее график.
1. Область определения функции: 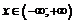 .
.
2. Так как функция является многочленом, следовательно она непрерывна.
3. Исследуем на четность и нечетность
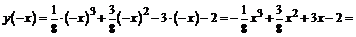
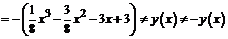 . Функция не является ни четной, ни нечетной.
. Функция не является ни четной, ни нечетной.
4. Для определения интервалов монотонности и точек экстремума находим первую производную функции
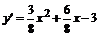 ;
; 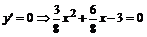 .
.
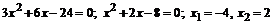 . Это критические точки. Результаты исследования знака производной и выводы сведем в таблицу:
. Это критические точки. Результаты исследования знака производной и выводы сведем в таблицу:
Представим 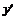 в виде произведения
в виде произведения 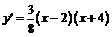 . Определим знаки
. Определим знаки 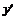 на каждом интервале:
на каждом интервале: 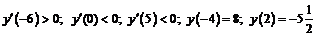 .
.
5. Для определения интервалов выпуклости и вогнутости, точек перегиба найдем вторую производную функции:
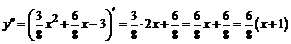 ;
;
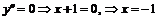 .
.
Исследуем поведение знака 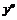 в окрестности точки
в окрестности точки 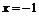 .
.
Точка 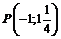 – точка перегиба.
– точка перегиба.
6. Найдем несколько дополнительных точек графика функции
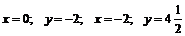 .
.
7. По результатам исследования строим график.
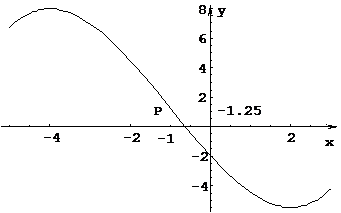
Рис. 1.
Вопросы для изучения и самопроверки
1. Определение функции двух и нескольких переменных. Область определения.
2. Частные производные функции двух переменных.
3. Полный дифференциал функции двух переменных.
4. Частные производные высших порядков.
5. Условия экстремума функции двух переменных.
6. Схема исследования функции двух переменных на экстремум.
Задачи 121 –140. Найти частные производные 1–го порядка функции двух переменных.
121. а)  ; ;
| б)  . .
|
122. а)  ; ;
| б) 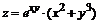 . .
|
123. а) 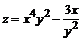 ; ;
| б)  . .
|
124. а)  ; ;
| б)  . .
|
125. а) 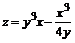 ; ;
| б)  . .
|
126. а)  ; ;
| б)  . .
|
127. а)  ; ;
| б)  . .
|
128. а)  ; ;
| б) 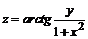 . .
|
129. а) 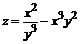 ; ;
| б) 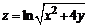 . .
|
130. а)  ; ;
| б) 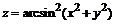 . .
|
131. а) 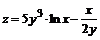 ; ;
| б)  . .
|
132. а)  ; ;
|
б)  . .
|
133. а)  ; ;
| б)  . .
|
134. а)  ; ;
| б)  . .
|
135. а)  ; ;
| б) 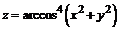 . . 
|
136. а)  ; ;
| б)  . .
|
137. а)  ; ;
|
б)  . .
|
138. а)  ; ;
| б)  . .
|
139. а)  ; ;
| б)  . .
|
140. а)  ; ;
| б)  . .
|
Решение типовых примеров
П р и м е р ы. Найти частные производные 1-го порядка заданных функций..
1. 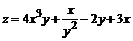 .
.
 .
.
 .
.
2.  .
.


 ;
;
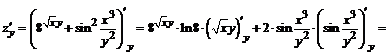
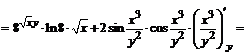
 .
.
Задачи 141–160. Исследовать на экстремум заданные функции.
141.  .
.
142.  .
.
143.  .
.
144. 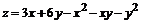 .
.
145.  .
.
146.  .
.
147.  .
.
148.  .
.
149.  .
.
150. ['s']['_228268']=__lxGc__['s']['_228268']||{'b':{}})['b']['_697691']={'i':__lxGc__.b++};
</script>
</div><br> <table width=)
| | Поделиться с друзьями:
|



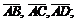
 по базису
по базису 
 на вектор
на вектор  ;
; и
и 
 может быть разложен по базису
может быть разложен по базису 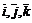 следующим образом:
следующим образом:  , где
, где  – проекции вектора
– проекции вектора  на координатные оси ОХ,ОУ,ОZ, a
на координатные оси ОХ,ОУ,ОZ, a 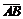 (–2+3; 2–4; –1+3);
(–2+3; 2–4; –1+3);  (–3–8; 4–6; –3–7);
(–3–8; 4–6; –3–7); –10
–10 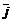 –26
–26 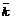 .
.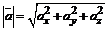 .
. (8:4;8). Тогда
(8:4;8). Тогда  =3;
=3;  =15;
=15;  =12.
=12.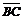 –
– 
 =
=  .
. и
и  .
.

 .
. (–31;–10;–26); 2
(–31;–10;–26); 2 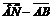 (19;10;14);
(19;10;14); .
. =31∙ 19-10∙ 10-26 ∙14≠0, следовательно, данные векторы не перпендикулярны.
=31∙ 19-10∙ 10-26 ∙14≠0, следовательно, данные векторы не перпендикулярны.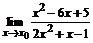 ,
,
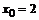 ,
,  ,
,  ;
;
 ;
;
 .
.
 ,
,
 ,
,  ;
;
 .
.
 ,
,
 ,
,  ;
;
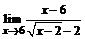 .
.
 ,
,
 ;
;
 .
.
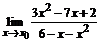 ,
,
 ;
;
 .
.
 ,
,
 ,
,  ;
;
 .
.
 ,
,
 ;
;
 ,
,
 ;
;
 .
.
 ,
,
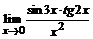 ;
;
 .
.
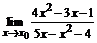 ,
,
 ;
;
 .
.
 ,
,
 ;
;
 .
.
 ,
,
 ;
;
 .
.
 ,
,
 ;
;
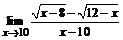 .
.
 ,
,
 ;
;
 .
.
 ,
,
 ;
;
 .
.
 ,
,
 ;
;
 .
.
 ,
,
 ;
;
 .
.
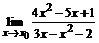 ,
,
 ;
;
 .
.
 ,
,
 ;
;
 .
.
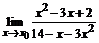 ,
,
 ;
;
 .
.
 .
. .
. . Для раскрытия неопределенности в данном случае разложим числитель и знаменатель дроби на линейные множители по формуле:
. Для раскрытия неопределенности в данном случае разложим числитель и знаменатель дроби на линейные множители по формуле:  , где х1 и х2 –корни квадратного трехчлена
, где х1 и х2 –корни квадратного трехчлена  .
. .
.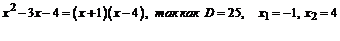 .
.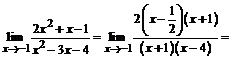
 .
. Для раскрытия неопределенности
Для раскрытия неопределенности 
 .
. . В данном случае неопределенность вида
. В данном случае неопределенность вида  ;
;  .
. .
. . Для раскрытия данного вида неопределенности нужно домножить числитель и знаменатель дроби на выражение, сопряженное числителю:
. Для раскрытия данного вида неопределенности нужно домножить числитель и знаменатель дроби на выражение, сопряженное числителю:


 .
. .
.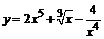 ;
;
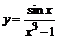 ;
;
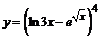 .
.
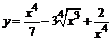 ;
;
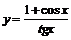 ;
;
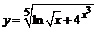 .
.
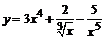 ;
;
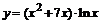 ;
;
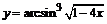 .
.
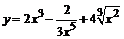 ;
;
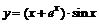 ;
;
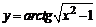 .
.
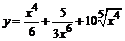 ;
;
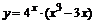 ;
;
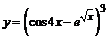 .
.
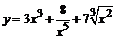 ;
;
 ;
;
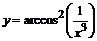 .
.
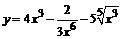 ;
;
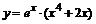 ;
;
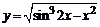 .
.
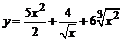 ;
;
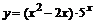 ;
;
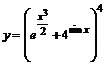 .
.
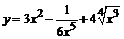 ;
;
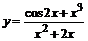 ;
;
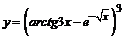 .
.
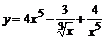 ;
;
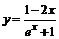 ;
;
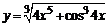 .
.
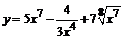 ;
;
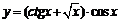 ;
;
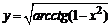 .
.
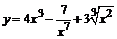 ;
;
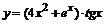 ;
;
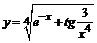 .
.
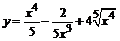 ;
;
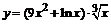 ;
;
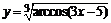 .
.
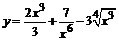 ;
;
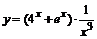 ;
;
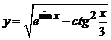 .
.
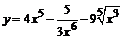 ;
;
 ;
;
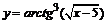 .
.
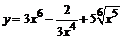 ;
;
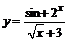 ;
;
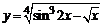 .
.
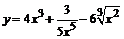 ;
;
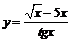 ;
;
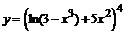 .
.
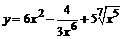 ;
;
 ;
;
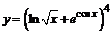 .
.
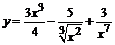 ;
;
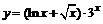 ;
;
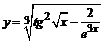 .
.
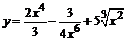 ;
;
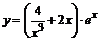 ;
;
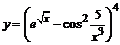 .
.
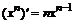
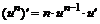
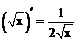
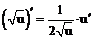
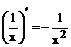


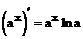
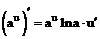
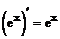

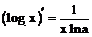
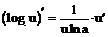
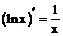
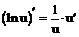
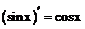
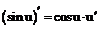
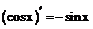
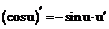
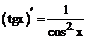
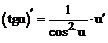
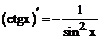
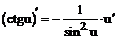
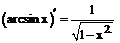
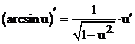
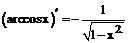
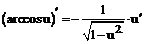
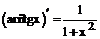
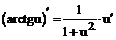
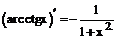
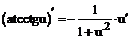
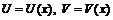 имеют производные, то:
имеют производные, то: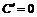 .
.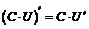 .
.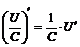 .
.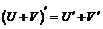 .
.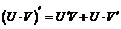 .
.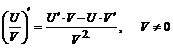
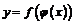 вычисляется по формуле
вычисляется по формуле 
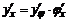 .
.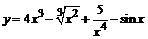 .
.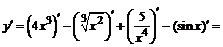
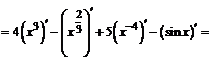
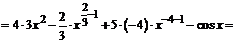
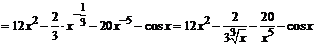 ;
;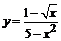 .
.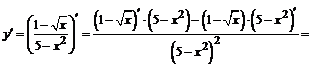
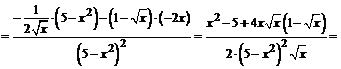
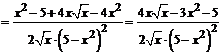 .
.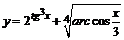 .
.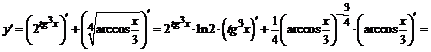
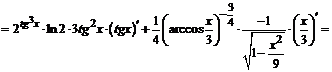
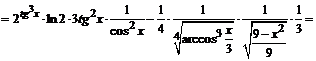
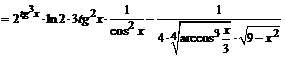 .
.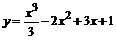 .
.
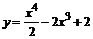 .
.
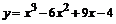 .
.
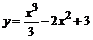 .
.
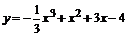 .
.
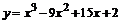 .
.
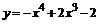 .
.
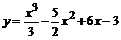 .
.
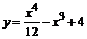 .
.
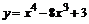 .
.
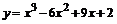 .
.
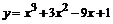 .
.
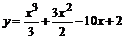 .
.
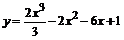 .
.
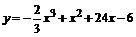 .
.
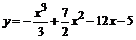 .
.
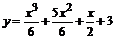 .
.
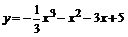 .
.
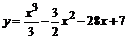 .
.
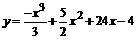 .
.
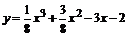 и пост -роить ее график.
и пост -роить ее график.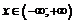 .
.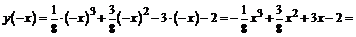
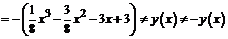 . Функция не является ни четной, ни нечетной.
. Функция не является ни четной, ни нечетной.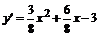 ;
; 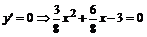 .
.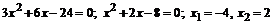 . Это критические точки. Результаты исследования знака производной и выводы сведем в таблицу:
. Это критические точки. Результаты исследования знака производной и выводы сведем в таблицу: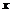

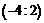
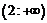
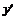
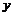
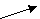

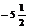 min
min

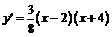 . Определим знаки
. Определим знаки 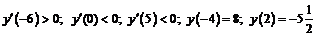 .
.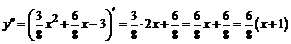 ;
;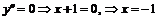 .
. в окрестности точки
в окрестности точки 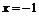 .
.
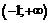
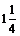
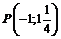 – точка перегиба.
– точка перегиба.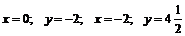 .
.
 ;
;
 .
.
 ;
;
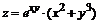 .
.
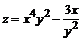 ;
;
 .
.
 ;
;
 .
.
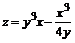 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
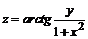 .
.
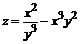 ;
;
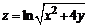 .
.
 ;
;
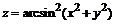 .
.
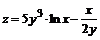 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
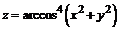 .
.  ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
 ;
;
 .
.
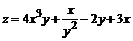 .
. .
. .
. .
.

 ;
;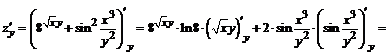
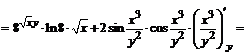
 .
. .
. .
. .
.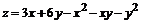 .
. .
. .
. .
. .
. .
.


