

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
Случайные ошибки представляют не что иное, как случайные события по теории вероятностей. Гаусс, рассматривая случайные события, установил нормальный закон распределения случайной величины, который применим и для результатов измерений при наличии случайных ошибок Δxi:
__ (-Δx2i/2σ2)
f(Δxi) = (1/ σ2 √2π) e (3)
 |
Рис. 1.
Нормальная кривая разделяется на три зоны, каждой из которых соответствует определенная вероятность попадания случайной величины. В интервал от xср – s до xср + s попадает 68% всех измерений. В интервале от xср– 2s до xср+ 2s то есть с удвоенной стандартной ошибкой, укладывается 95% всех измерений, а в интервал от xср – 3s до xср +3s – 99,7%. Только 0,003% всех измерений выходит за пределы интервала (xср – 3s, xср +3s). Практически вероятность таких измерений равна нулю. Таким образом, удобство применения стандартной ошибки в качестве основного выражения погрешности измерения заключается в том, что ей соответствует математически обоснованная определенная вероятность, называемая доверительной вероятностью, а соответствующий ей интервал называется доверительным интервалом.
Элементы теории случайных погрешностей. Погрешность прибора как случайная величина.Связь систематической погрешности с величиной математического ожидания.
При наличии случайных погрешностей измерений прибегают к многократным наблюдениям и последующей статистической обработке их результатов. При этом результаты наблюдений и измерений и случайные погрешности рассматриваются как случайные величины, то есть величины, которые характеризуют случайное явление и в результате измерений принимают то или иное значение.
Наибольший практический интерес представляет начальный момент первого порядка - математическое ожидание случайной величины m1 (k=1):



Математическое ожидание определяет положение центра группирования случайной величины, вокруг которого наблюдается ее рассеяние. Экспериментальной оценкой математического ожидания при многократных измерениях является среднее арифметическое значение измеряемой величины.
Элементы теории случайных погрешностей. Среднеквадратичное отклонение, как величина, характеризующая разброс случайных погрешностей. Понятие о нормированной (единичной) функции нормального распределения. Как перейти от нормированной функции нормального распределения (функции, у которой сигма равна единице) к функции с произвольным значением сигма.
Оценка S среднего квадратического отклонения (СКО) дается формулой:
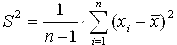
Эта оценка характеризует рассеяние единичных результатов измерений в ряду равноточных измерений одной и той же величины около их среднего значения.
Другими оценками рассеяния результатов в ряду измерений являются размах (разница между наибольшим и наименьшим значением), модуль средней арифметической погрешности (арифметическая сумма погрешностей, деленная на число измерений) и доверительная граница погрешности (подробно рассматривается ниже).
СКО является наиболее удобной характеристикой погрешности в случае ее дальнейшего преобразования. Например, для нескольких некоррелированных слагаемых СКО суммы определяется по формуле:
 .
.
|
|
|

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!