Сплошной средой называется физическое тело, свойства которого в соседних точках мало отличаются. Это означает, что физические величины, определяющие рассматриваемые свойства сплошной среды, близки в соседних точках. Традиционными примерами таких тел являются жидкости или газы.
Упругими называют деформации, исчезающие после снятия вызвавшей их нагрузки. Остаточные (пластические) – часть полных деформаций не исчезающая после разгружения элемента.
При всем многообразии случаев произвольную деформацию тела можно свести к двум элементарным деформациям — растяжению (сжатию) и сдвигу.
Модуль упругости является количественной характеристикой жесткости материалаи определяется, как тангенс угла наклона α на прямолинейном отрезке диаграммы растяжения OA (рис.4.5).Модуль упругости определяется силами межатомного взаимодействия и практически не зависит от состава и структуры материала. Количественной характеристикой упругости является условный предел упругости - напряжение, при котором остаточная микродеформация равна определенной заданной величине в пределах от 0,001 до 0,05%. Количественными характеристиками прочности материала являются предел текучести и предел прочности. В зависимости от вида получаемой диаграммы растяжения для различных материалов определяют либо условный предел текучести, либо физический предел текучести.Условный предел текучести – напряжение, соответствующее условно заданной величине деформации, равной 0,2%.
Закон Гука: для малых деформаций относительное удлинение e прямо пропорционально вызывающему его напряжению s:. 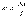 –относительное удлинение (относительная деформация).
–относительное удлинение (относительная деформация).  где Е – коэффициент пропорциональности,называется модулем Юнга.: модуль Юнгачисленно равен напряжению, вызывающему относительное удлинение, равное единице.При относительном удлинении, равном единице
где Е – коэффициент пропорциональности,называется модулем Юнга.: модуль Юнгачисленно равен напряжению, вызывающему относительное удлинение, равное единице.При относительном удлинении, равном единице 
 , абсолютное удлинение l = l, откуда получаем: модуль Юнга численно равен тому напряжению, которое растягивает стержень вдвое. На самом деле большинство материалов разрушается раньше, чем они будут растянуты вдвое, поэтому фактически нельзя приложить к стержню напряжение численно равное модулю Юнга.
, абсолютное удлинение l = l, откуда получаем: модуль Юнга численно равен тому напряжению, которое растягивает стержень вдвое. На самом деле большинство материалов разрушается раньше, чем они будут растянуты вдвое, поэтому фактически нельзя приложить к стержню напряжение численно равное модулю Юнга.
Вычислим энергию упруго растянутого (сжатого) стержня. При растяжении на стержень необходимо действовать силой, величина которой определяется выражением (113). Работа этой силы равна  где буквой х обозначено абсолютное удлинение стержня, которое в процессе деформации изменяется от 0 до Δl. Сила f, соответствующая удлинению х, согласно (113) равна
где буквой х обозначено абсолютное удлинение стержня, которое в процессе деформации изменяется от 0 до Δl. Сила f, соответствующая удлинению х, согласно (113) равна
 Следовательно,
Следовательно,  Умножая числитель и знаменатель полученного выражения на l, заменяя затем отношение Δl/l относительным удлинением ε и учитывая, наконец, что Sl дает объем стержня V, получим:
Умножая числитель и знаменатель полученного выражения на l, заменяя затем отношение Δl/l относительным удлинением ε и учитывая, наконец, что Sl дает объем стержня V, получим:  (121)Введем в рассмотрение плотность энергии u, которую определим как отношение энергии ΔU к тому объему ΔV, в котором она заключена:
(121)Введем в рассмотрение плотность энергии u, которую определим как отношение энергии ΔU к тому объему ΔV, в котором она заключена: 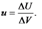 Поскольку в нашем случае стержень однороден и деформация является равномерной, т. е. одинаковой в разных точках стержня, энергия (121) распределена в стержне также равномерно с постоянной плотностью. Поэтому можно считать:
Поскольку в нашем случае стержень однороден и деформация является равномерной, т. е. одинаковой в разных точках стержня, энергия (121) распределена в стержне также равномерно с постоянной плотностью. Поэтому можно считать:
 (122)Выражение (122) дает плотность энергии упругой деформации при растяжении (или при сжатии). Аналогичным образом можно получить, что плотность энергии упругой деформации при сдвиге равна
(122)Выражение (122) дает плотность энергии упругой деформации при растяжении (или при сжатии). Аналогичным образом можно получить, что плотность энергии упругой деформации при сдвиге равна 





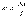 –относительное удлинение (относительная деформация).
–относительное удлинение (относительная деформация).  где Е – коэффициент пропорциональности,называется модулем Юнга.: модуль Юнгачисленно равен напряжению, вызывающему относительное удлинение, равное единице.При относительном удлинении, равном единице
где Е – коэффициент пропорциональности,называется модулем Юнга.: модуль Юнгачисленно равен напряжению, вызывающему относительное удлинение, равное единице.При относительном удлинении, равном единице 
 , абсолютное удлинение l = l, откуда получаем: модуль Юнга численно равен тому напряжению, которое растягивает стержень вдвое. На самом деле большинство материалов разрушается раньше, чем они будут растянуты вдвое, поэтому фактически нельзя приложить к стержню напряжение численно равное модулю Юнга.
, абсолютное удлинение l = l, откуда получаем: модуль Юнга численно равен тому напряжению, которое растягивает стержень вдвое. На самом деле большинство материалов разрушается раньше, чем они будут растянуты вдвое, поэтому фактически нельзя приложить к стержню напряжение численно равное модулю Юнга. где буквой х обозначено абсолютное удлинение стержня, которое в процессе деформации изменяется от 0 до Δl. Сила f, соответствующая удлинению х, согласно (113) равна
где буквой х обозначено абсолютное удлинение стержня, которое в процессе деформации изменяется от 0 до Δl. Сила f, соответствующая удлинению х, согласно (113) равна Следовательно,
Следовательно,  Умножая числитель и знаменатель полученного выражения на l, заменяя затем отношение Δl/l относительным удлинением ε и учитывая, наконец, что Sl дает объем стержня V, получим:
Умножая числитель и знаменатель полученного выражения на l, заменяя затем отношение Δl/l относительным удлинением ε и учитывая, наконец, что Sl дает объем стержня V, получим:  (121)Введем в рассмотрение плотность энергии u, которую определим как отношение энергии ΔU к тому объему ΔV, в котором она заключена:
(121)Введем в рассмотрение плотность энергии u, которую определим как отношение энергии ΔU к тому объему ΔV, в котором она заключена: 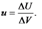 Поскольку в нашем случае стержень однороден и деформация является равномерной, т. е. одинаковой в разных точках стержня, энергия (121) распределена в стержне также равномерно с постоянной плотностью. Поэтому можно считать:
Поскольку в нашем случае стержень однороден и деформация является равномерной, т. е. одинаковой в разных точках стержня, энергия (121) распределена в стержне также равномерно с постоянной плотностью. Поэтому можно считать: (122)Выражение (122) дает плотность энергии упругой деформации при растяжении (или при сжатии). Аналогичным образом можно получить, что плотность энергии упругой деформации при сдвиге равна
(122)Выражение (122) дает плотность энергии упругой деформации при растяжении (или при сжатии). Аналогичным образом можно получить, что плотность энергии упругой деформации при сдвиге равна 



