Функция распределения системы двух СВ
Это вероятность произведения двух событий: 
Свойства  : 1)
: 1)  причем
причем 
2)  - неубывающая по каждому аргументу
- неубывающая по каждому аргументу
3)  - непрерывна слева по каждому аргументу
- непрерывна слева по каждому аргументу
4) Вероятность попадания случайной точки (X, Y) в прямоугольник:  ≥ 0
≥ 0
5)  одномерные функции распределения.
одномерные функции распределения.
Определение. Случайные величины X, Y называются независимыми, если  .
.
Для дискретных случайных величин X, Y из их независимостиследует независимость любой пары событий: X=xi, Y=yj, где xi, yj – всевозможные значения СВ. Справедливо и обратное утверждение.
Пример. Экспоненциальное распределение системы независимых СВ: 
2.4.3. Совместное распределение вероятностей
Системы двух ДСВ.
Оно задается матрицей (таблицей) значений вероятностей произведения событий:  для различных
для различных  .
.
При этом 
Примером системы двух дискретных СВ является число пропущенных студентом занятий(X)и оценка на экзамене (Y).
Если заданы  , то
, то 
Условные вероятности:

Если две ДСВ независимы, то  и наоборот.
и наоборот.
Пример 1. Пусть имеется система из двух случайных величин, каждая из которых может принимать значения 1 (успех) или 0 (неудача). Известна таблица
вероятностей  .
.
Тогда  ;
;
 ;
;
Таблица значений функции распределения  имеет вид:
имеет вид:
|
хi
| yj
|
|
|
| y >1
|
|
|
|
|
|
|
|
| 0,3
| 0,5
|
| x>1
|
| 0,4
|
|
Действительно,  = Р(X<0, Y<1) = 0;
= Р(X<0, Y<1) = 0;  = Р(X<1, Y<1) = Р(X=0,Y=0) = 0,3;
= Р(X<1, Y<1) = Р(X=0,Y=0) = 0,3; 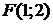 = Р(X<1, Y<2) = Р(X<1) = Р(X=0)=р1= 0,5 и т.д.
= Р(X<1, Y<2) = Р(X<1) = Р(X=0)=р1= 0,5 и т.д.
Величины X и Y – зависимы. Для того, чтобы сделать такой вывод, достаточно заметить, что, например, р11 ≠ р1·q1 или  .
.
Пример 2. Пусть дано распределение системы двух случайных величин:
|
хi
| yj
|
|
|
|
|
| 0,18
| 0,42
| |
|
| 0,12
| 0,28
| |
Тогда  ; р2= 0,4; q1= 0,3; q2= 0,7. Величины X и Y – независимы, так как р11 =0,18= р1·q1 =0,6∙0,3 и т. д.
; р2= 0,4; q1= 0,3; q2= 0,7. Величины X и Y – независимы, так как р11 =0,18= р1·q1 =0,6∙0,3 и т. д.
2.4.4. Плотность распределения системы двух НСВ
Это частная смешанная производная второго порядка от функции распределения: 
Если задана плотность  , то:
, то: 
Свойства  : 1)
: 1)  2)
2) 
3) Вероятность попадания случайной точки в заданную область D:

4) Одномерные плотности распределения:

5) Если две НСВ независимы, то 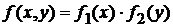 и наоборот.
и наоборот.
Условные плотности:  ;
; 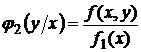 .
.
2.4.5. Математические ожидания и дисперсии.
В случае, когда задано совместное распределение вероятностей системы двух ДСВ, математические ожидания и дисперсии определяются по формулам:

В случае двух НСВ знаки å заменяются на ò, а рij – на  .
.
Условное математическое ожидание для НСВ:

Оно называется уравнением (функцией) регрессии Y на X.
Аналогично определяется уравнение регрессии X на Y, т. е. 
Условная дисперсия для НСВ:

Аналогично определяется  .
.
Для ДСВ знак ∫ заменяется на Σ, а  – на
– на 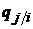 .
.
Условные математическое ожидание и дисперсия характеризуют случайную величину Y при фиксированном значении параметра x или наоборот.
2.4.6. Показатели статистической зависимости двух СВ
1. Ковариация (корреляционный момент):

В частности, для системы из двух непрерывных случайных величин:
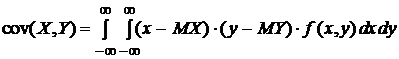
Свойства: 1)  2) КХХ≡
2) КХХ≡ 
3) 
4) 
5) Если X и Y – независимы, то они некоррелированы, т. е. 
(обратное бывает не справедливо).
Эти свойства легко доказываются, если воспользоваться общей формулой для ковариации и свойствами математического ожидания, в частности, если вспомнить, что для независимых СВ  .
.
Пример. Пусть Y и X связаны зависимостью  , где
, где
 независимые СВ,
независимые СВ,  . Тогда
. Тогда  .
.
Вывод: зависимые X и Y оказались некоррелированными.
2. Коэффициент корреляции:

Свойства: 1)  , 2)
, 2) 
3)  тогда и только тогда, когда
тогда и только тогда, когда  где
где  причем
причем  , если
, если  и
и  , если
, если 
4) Для независимых X и Y  (так как
(так как  )
)
Докажем второе и третье свойство. Пусть  , где
, где  независимые СВ. Тогда, используя свойства дисперсии, получим: DY=a2DX+D
независимые СВ. Тогда, используя свойства дисперсии, получим: DY=a2DX+D  , так как Db= 0; D(X±Y)=D(X±
, так как Db= 0; D(X±Y)=D(X±  )=
)=  + D
+ D  .
.
Применим формулы: cov(X,Y)=  ; D(X±Y)=DX+DY±2cov(X,Y).
; D(X±Y)=DX+DY±2cov(X,Y).
Подставляя в последнюю предыдущие выражения, получим:
 + D
+ D  =DX+a2DX+D
=DX+a2DX+D  ±2
±2  ;
;
 = ±
= ±  . Отсюда
. Отсюда 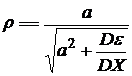 .
.
Так как знаменатель не меньше, чем  , то получаем неравенство:
, то получаем неравенство:  . Если
. Если  т.е. D
т.е. D  =0, то имеем:
=0, то имеем:  .
.
Коэффициент корреляции характеризует степень тесноты линейной связи между двумя случайными величинами.
Общий случай
Пусть имеется система, состоящая из k случайных величин:  . Пусть известна функция распределения
. Пусть известна функция распределения  или плотность распределения
или плотность распределения  . На практике большое распространение получило нормальное распределение, плотность которого имеет вид:
. На практике большое распространение получило нормальное распределение, плотность которого имеет вид:
f (x1,x2,…,xk) =  ,
,
где (х-а) и (х-а)′ – вектор-столбец, соответственно, вектор-строка переменных, состоящие из элементов хi-a (i=1,2,…,k);
B-1 – матрица, обратная ковариационной матрице B= (Кij) ≡ (cov(Xi,Xj));
ΔB– определитель матрицы B.
В частности, при k =2 имеем:
B=  ; B-1=
; B-1=  ; ΔB=
; ΔB=  ;
;
(х-а)′ B-1 (х-а) = 
Подставляя полученные выражения в формулу для f (x1,x2,…,xk) при k= 2, получим выражение для двумерной плотности вероятности нормально распределенной случайной величины, приведенное ранее.
При k≥ 3, по аналогии с тем, как одномерные распределения выражаются через двумерные, можно получить двумерные распределения для каждой пары Xi, Xj (i ≠ j): для НСВ – плотности  , для ДСВ – матрицы (
, для ДСВ – матрицы ( ) вероятностей произведения событий:
) вероятностей произведения событий:  . Определяя для каждой пары ковариации и коэффициенты корреляции, получим ковариационную матрицу (Кij), по главной диагонали которой будут стоять дисперсии, и корреляционную матрицу
. Определяя для каждой пары ковариации и коэффициенты корреляции, получим ковариационную матрицу (Кij), по главной диагонали которой будут стоять дисперсии, и корреляционную матрицу  , по главной диагонали которой будут стоять единицы, причем Кij = Кji и
, по главной диагонали которой будут стоять единицы, причем Кij = Кji и  =
=  .
.
Функция распределения зависит от условий проведения испытаний или наблюдений. Значит, от этих условий зависят и  . Пусть, например, испытания будут проведены теперь при некоторых фиксированных значениях всех случайных величин, кроме X1 и X2. Если
. Пусть, например, испытания будут проведены теперь при некоторых фиксированных значениях всех случайных величин, кроме X1 и X2. Если 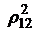 при этом уменьшится, то можно сделать вывод, что взаимозависимость между X1 и X2 во многом (или даже в значительной степени) была вызвана действием других (ныне фиксированных) факторов. И наоборот, если
при этом уменьшится, то можно сделать вывод, что взаимозависимость между X1 и X2 во многом (или даже в значительной степени) была вызвана действием других (ныне фиксированных) факторов. И наоборот, если 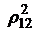 увеличится, то это будет означать, что другие факторы маскировали истинную взаимозависимость между X1 и X2. Поэтому, наряду с
увеличится, то это будет означать, что другие факторы маскировали истинную взаимозависимость между X1 и X2. Поэтому, наряду с  (их называют коэффициентами парной корреляции) используют и другие показатели статистической зависимости: множественные коэффициенты корреляции и частные коэффициенты корреляции.
(их называют коэффициентами парной корреляции) используют и другие показатели статистической зависимости: множественные коэффициенты корреляции и частные коэффициенты корреляции.
Распределение Пирсона
Пусть 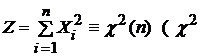 читается: «хи-квадрат»), где
читается: «хи-квадрат»), где 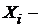 независимые СВ,
независимые СВ, 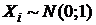 при
при 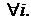 Распределение этой случайной величины называется распределением Пирсона (или распределением c2) с n степенями свободы. Плотность распределения СВ c2 имеет вид:
Распределение этой случайной величины называется распределением Пирсона (или распределением c2) с n степенями свободы. Плотность распределения СВ c2 имеет вид:
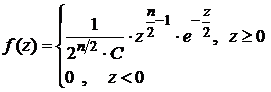
где С = Г  – значение гамма-функции Г (х) в точке n /2, Г(х)
– значение гамма-функции Г (х) в точке n /2, Г(х) 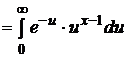 –табулированная гамма-функция. В частности, если х – целое число, то Г(х)= х! На рис.10 изображены плотности вероятности при n=2 и n=6.
–табулированная гамма-функция. В частности, если х – целое число, то Г(х)= х! На рис.10 изображены плотности вероятности при n=2 и n=6.
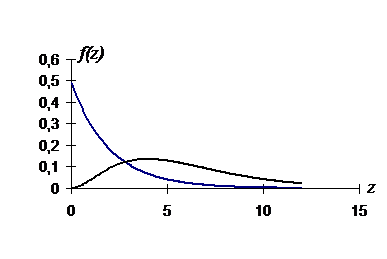
Рис10. Плотность распределения величины c2
При n=2 f(z) –функция монотонная. Математическое ожидание МZ=n, дисперсия DZ=2n.
Распределение Пирсона (оно, как видно из формулы, – однопараметрическое) является частным случаем двухпараметрического гамма-распределения, часто используемого на практике, когда СВ не может принимать отрицательные значения.
В табл.3П приложения содержатся квантили 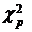 плотности распределения случайной величины
плотности распределения случайной величины 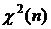 для различных значений степени свободы n≡k и различных значений вероятности р т.е. такие значения
для различных значений степени свободы n≡k и различных значений вероятности р т.е. такие значения 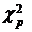 , при которых справедливо равенство
, при которых справедливо равенство 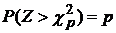 .
.
Распределение Стьюдента.
Пусть 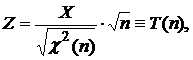 где X и
где X и 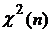 независимы,
независимы, 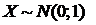 .
.
Распределение этой случайной величины называется распределением Стьюдента (или Т-распределением) с n степенями свободы.
Плотность распределения Стьюдента имеет вид (рис. 11):
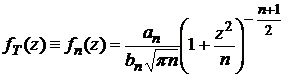 ,
,
где an = Г 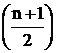 , bn = Г
, bn = Г 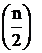 , Г(х) – гамма-функция.
, Г(х) – гамма-функция.
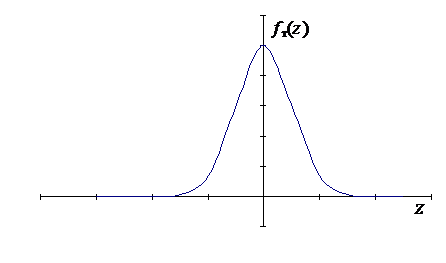
Рис.11. Плотность распределения Стьюдента
Математическое ожидание, коэффициент асимметрии и коэффициент эксцесса случайной величины Z равны 0, дисперсия DZ = 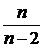 при n >2. Из этого следует, что распределение Стьюдента имеет чуть больший разброс по сравнению со стандартным нормальным N (0;1). При n ® ¥ fn (z) сходится к нормальному с математическим ожиданием а =0 и дисперсией
при n >2. Из этого следует, что распределение Стьюдента имеет чуть больший разброс по сравнению со стандартным нормальным N (0;1). При n ® ¥ fn (z) сходится к нормальному с математическим ожиданием а =0 и дисперсией 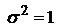 .
.
В табл.2П приложения содержатся квантили tp плотности распределения случайной величины T (n) для различных значений степени свободы n ≡ k и различных значений вероятности р, т.е. такие значения tp, при которых справедливо равенство 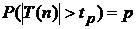 .
.
Распределение Фишера.
Распределением Фишера (F -распределением) с m и n степенями свободы называется распределение случайной величины 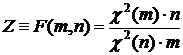 , где
, где 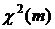 и
и 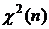 – независимые случайные величины. Из формулы видно, что
– независимые случайные величины. Из формулы видно, что 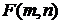 ≥ 0. Плотность распределения Фишера fF (z) также выражается через гамма-функцию (ее выражение, ввиду громоздкости, не приводится). Следует заметить, что fF (z) имеет один максимум, при z → ∞ fF (z) → 0, а при z ≤ 0 fF (z)=0. В табл.4П приложения содержатся правосторонние квантили плотности распределения случайной величины
≥ 0. Плотность распределения Фишера fF (z) также выражается через гамма-функцию (ее выражение, ввиду громоздкости, не приводится). Следует заметить, что fF (z) имеет один максимум, при z → ∞ fF (z) → 0, а при z ≤ 0 fF (z)=0. В табл.4П приложения содержатся правосторонние квантили плотности распределения случайной величины 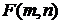
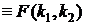 для различных значений степеней свободы, т.е. такие значения
для различных значений степеней свободы, т.е. такие значения 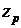 , при которых
, при которых 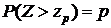 (р= 0,05).
(р= 0,05).
Распределения хи-квадрат, Стьюдента и Фишера широко используются в математической статистике. Значения квантилей этих и других распределений в зависимости от вероятностей попадания случайной величины в интервал, а также от числа степенейсвободы можно найти не только в учебниках и справочниках, но и в компьютере при наличии необходимого программного обеспечения.
Функция распределения системы двух СВ
Это вероятность произведения двух событий: 
Свойства  : 1)
: 1)  причем
причем 
2)  - неубывающая по каждому аргументу
- неубывающая по каждому аргументу
3)  - непрерывна слева по каждому аргументу
- непрерывна слева по каждому аргументу
4) Вероятность попадания случайной точки (X, Y) в прямоугольник:  ≥ 0
≥ 0
5)  одномерные функции распределения.
одномерные функции распределения.
Определение. Случайные величины X, Y называются независимыми, если  .
.
Для дискретных случайных величин X, Y из их независимостиследует независимость любой пары событий: X=xi, Y=yj, где xi, yj – всевозможные значения СВ. Справедливо и обратное утверждение.
Пример. Экспоненциальное распределение системы независимых СВ: 
2.4.3. Совместное распределение вероятностей
Системы двух ДСВ.
Оно задается матрицей (таблицей) значений вероятностей произведения событий:  для различных
для различных  .
.
При этом 
Примером системы двух дискретных СВ является число пропущенных студентом занятий(X)и оценка на экзамене (Y).
Если заданы  , то
, то 
Условные вероятности:

Если две ДСВ независимы, то  и наоборот.
и наоборот.
Пример 1. Пусть имеется система из двух случайных величин, каждая из которых может принимать значения 1 (успех) или 0 (неудача). Известна таблица
вероятностей  .
.
Тогда  ;
;
 ;
;
Таблица значений функции распределения  имеет вид:
имеет вид:
|
хi
| yj
|
|
|
| y >1
|
|
|
|
|
|
|
|
| 0,3
| 0,5
|
| x>1
|
| 0,4
|
|
Действительно,  = Р(X<0, Y<1) = 0;
= Р(X<0, Y<1) = 0;  = Р(X<1, Y<1) = Р(X=0,Y=0) = 0,3;
= Р(X<1, Y<1) = Р(X=0,Y=0) = 0,3; 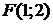 = Р(X<1, Y<2) = Р(X<1) = Р(X=0)=р1= 0,5 и т.д.
= Р(X<1, Y<2) = Р(X<1) = Р(X=0)=р1= 0,5 и т.д.
Величины X и Y – зависимы. Для того, чтобы сделать такой вывод, достаточно заметить, что, например, р11 ≠ р1·q1 или  .
.
Пример 2. Пусть дано распределение системы двух случайных величин:
|
хi
| yj
|
|
|
|
|
| 0,18
| 0,42
| |
|
| 0,12
| 0,28
| |
Тогда  ; р2= 0,4; q1= 0,3; q2= 0,7. Величины X и Y – независимы, так как р11 =0,18= р1·q1 =0,6∙0,3 и т. д.
; р2= 0,4; q1= 0,3; q2= 0,7. Величины X и Y – независимы, так как р11 =0,18= р1·q1 =0,6∙0,3 и т. д.
2.4.4. Плотность распределения системы двух НСВ
Это частная смешанная производная второго порядка от функции распределения: 
Если задана плотность  , то:
, то: 
Свойства  : 1)
: 1)  2)
2) 
3) Вероятность попадания случайной точки в заданную область D:

4) Одномерные плотности распределения:

5) Если две НСВ независимы, то 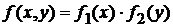 и наоборот.
и наоборот.
Условные плотности:  ;
; 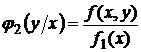 .
.
2.4.5. Математические ожидания и дисперсии.
В случае, когда задано совместное распределение вероятностей системы двух ДСВ, математические ожидания и дисперсии определяются по формулам:

В случае двух НСВ знаки å заменяются на ò, а рij – на  .
.
Условное математическое ожидание для НСВ:

Оно называется уравнением (функцией) регрессии Y на X.
Аналогично определяется уравнение регрессии X на Y, т. е. 
Условная дисперсия для НСВ:

Аналогично определяется  .
.
Для ДСВ знак ∫ заменяется на Σ, а  – на
– на 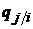 .
.
Условные математическое ожидание и дисперсия характеризуют случайную величину Y при фиксированном значении параметра x или наоборот.
2.4.6. Показатели статистической зависимости двух СВ
1. Ковариация (корреляционный момент):

В частности, для системы из двух непрерывных случайных величин:
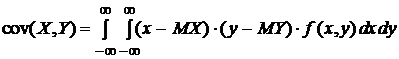
Свойства: 1)  2) КХХ≡
2) КХХ≡ 
3) 
4) 
5) Если X и Y – независимы, то они некоррелированы, т. е. 
(обратное бывает не справедливо).
Эти свойства легко доказываются, если воспользоваться общей формулой для ковариации и свойствами математического ожидания, в частности, если вспомнить, что для независимых СВ  .
.
Пример. Пусть Y и X связаны зависимостью  , где
, где
 независимые СВ,
независимые СВ,  . Тогда
. Тогда  .
.
Вывод: зависимые X и Y оказались некоррелированными.
2. Коэффициент корреляции:

Свойства: 1)  , 2)
, 2) 
3)  тогда и только тогда, когда
тогда и только тогда, когда  где
где  причем
причем  , если
, если  и
и  , если
, если 
4) Для независимых X и Y  (так как
(так как  )
)
Докажем второе и третье свойство. Пусть  , где
, где  независимые СВ. Тогда, используя свойства дисперсии, получим: DY=a2DX+D
независимые СВ. Тогда, используя свойства дисперсии, получим: DY=a2DX+D  , так как Db= 0; D(X±Y)=D(X±
, так как Db= 0; D(X±Y)=D(X±  )=
)=  + D
+ D  .
.
Применим формулы: cov(X,Y)=  ; D(X±Y)=DX+DY±2cov(X,Y).
; D(X±Y)=DX+DY±2cov(X,Y).
Подставляя в последнюю предыдущие выражения, получим:
 + D
+ D  =DX+a2DX+D
=DX+a2DX+D  ±2
±2  ;
;
 = ±
= ±  . Отсюда
. Отсюда 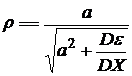 .
.
Так как знаменатель не меньше, чем  , то получаем неравенство:
, то получаем неравенство:  . Если
. Если  т.е. D
т.е. D  =0, то имеем:
=0, то имеем:  .
.
Коэффициент корреляции характеризует степень тесноты линейной связи между двумя случайными величинами.




 : 1)
: 1)  причем
причем 
 ≥ 0
≥ 0 одномерные функции распределения.
одномерные функции распределения. .
.
 для различных
для различных  .
.
 , то
, то 

 и наоборот.
и наоборот. .
. ;
; ;
; = Р(X<0, Y<1) = 0;
= Р(X<0, Y<1) = 0;  = Р(X<1, Y<1) = Р(X=0,Y=0) = 0,3;
= Р(X<1, Y<1) = Р(X=0,Y=0) = 0,3; 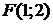 = Р(X<1, Y<2) = Р(X<1) = Р(X=0)=р1= 0,5 и т.д.
= Р(X<1, Y<2) = Р(X<1) = Р(X=0)=р1= 0,5 и т.д. .
. ; р2= 0,4; q1= 0,3; q2= 0,7. Величины X и Y – независимы, так как р11 =0,18= р1·q1 =0,6∙0,3 и т. д.
; р2= 0,4; q1= 0,3; q2= 0,7. Величины X и Y – независимы, так как р11 =0,18= р1·q1 =0,6∙0,3 и т. д.
 , то:
, то: 
 2)
2) 


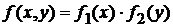 и наоборот.
и наоборот. ;
; 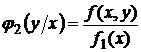 .
.
 .
.


 .
. – на
– на 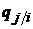 .
.
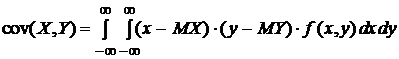
 2) КХХ≡
2) КХХ≡ 



 .
. , где
, где  независимые СВ,
независимые СВ,  . Тогда
. Тогда  .
.
 , 2)
, 2) 
 тогда и только тогда, когда
тогда и только тогда, когда  где
где  причем
причем  , если
, если  и
и  , если
, если 
 (так как
(так как  , где
, где  , так как Db= 0; D(X±Y)=D(X±
, так как Db= 0; D(X±Y)=D(X±  )=
)=  + D
+ D  ; D(X±Y)=DX+DY±2cov(X,Y).
; D(X±Y)=DX+DY±2cov(X,Y). ;
; = ±
= ± 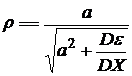 .
. , то получаем неравенство:
, то получаем неравенство:  . Пусть известна функция распределения
. Пусть известна функция распределения  или плотность распределения
или плотность распределения  . На практике большое распространение получило нормальное распределение, плотность которого имеет вид:
. На практике большое распространение получило нормальное распределение, плотность которого имеет вид: ,
, ; B-1=
; B-1=  ; ΔB=
; ΔB=  ;
;
 , для ДСВ – матрицы (
, для ДСВ – матрицы ( ) вероятностей произведения событий:
) вероятностей произведения событий:  . Определяя для каждой пары ковариации и коэффициенты корреляции, получим ковариационную матрицу (Кij), по главной диагонали которой будут стоять дисперсии, и корреляционную матрицу
. Определяя для каждой пары ковариации и коэффициенты корреляции, получим ковариационную матрицу (Кij), по главной диагонали которой будут стоять дисперсии, и корреляционную матрицу  , по главной диагонали которой будут стоять единицы, причем Кij = Кji и
, по главной диагонали которой будут стоять единицы, причем Кij = Кji и  =
=  .
.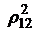 при этом уменьшится, то можно сделать вывод, что взаимозависимость между X1 и X2 во многом (или даже в значительной степени) была вызвана действием других (ныне фиксированных) факторов. И наоборот, если
при этом уменьшится, то можно сделать вывод, что взаимозависимость между X1 и X2 во многом (или даже в значительной степени) была вызвана действием других (ныне фиксированных) факторов. И наоборот, если 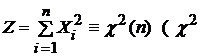 читается: «хи-квадрат»), где
читается: «хи-квадрат»), где 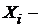 независимые СВ,
независимые СВ, 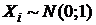 при
при 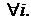 Распределение этой случайной величины называется распределением Пирсона (или распределением c2) с n степенями свободы. Плотность распределения СВ c2 имеет вид:
Распределение этой случайной величины называется распределением Пирсона (или распределением c2) с n степенями свободы. Плотность распределения СВ c2 имеет вид: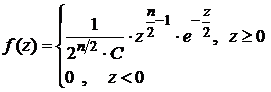
 – значение гамма-функции Г (х) в точке n /2, Г(х)
– значение гамма-функции Г (х) в точке n /2, Г(х) 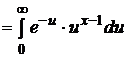 –табулированная гамма-функция. В частности, если х – целое число, то Г(х)= х! На рис.10 изображены плотности вероятности при n=2 и n=6.
–табулированная гамма-функция. В частности, если х – целое число, то Г(х)= х! На рис.10 изображены плотности вероятности при n=2 и n=6.
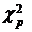 плотности распределения случайной величины
плотности распределения случайной величины 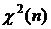 для различных значений степени свободы n≡k и различных значений вероятности р т.е. такие значения
для различных значений степени свободы n≡k и различных значений вероятности р т.е. такие значения 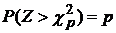 .
.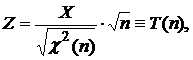 где X и
где X и 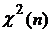 независимы,
независимы, 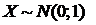 .
.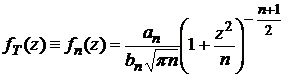 ,
,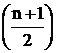 , bn = Г
, bn = Г 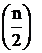 , Г(х) – гамма-функция.
, Г(х) – гамма-функция.
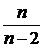 при n >2. Из этого следует, что распределение Стьюдента имеет чуть больший разброс по сравнению со стандартным нормальным N (0;1). При n ® ¥ fn (z) сходится к нормальному с математическим ожиданием а =0 и дисперсией
при n >2. Из этого следует, что распределение Стьюдента имеет чуть больший разброс по сравнению со стандартным нормальным N (0;1). При n ® ¥ fn (z) сходится к нормальному с математическим ожиданием а =0 и дисперсией 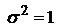 .
.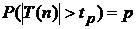 .
.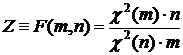 , где
, где 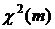 и
и 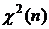 – независимые случайные величины. Из формулы видно, что
– независимые случайные величины. Из формулы видно, что 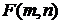 ≥ 0. Плотность распределения Фишера fF (z) также выражается через гамма-функцию (ее выражение, ввиду громоздкости, не приводится). Следует заметить, что fF (z) имеет один максимум, при z → ∞ fF (z) → 0, а при z ≤ 0 fF (z)=0. В табл.4П приложения содержатся правосторонние квантили плотности распределения случайной величины
≥ 0. Плотность распределения Фишера fF (z) также выражается через гамма-функцию (ее выражение, ввиду громоздкости, не приводится). Следует заметить, что fF (z) имеет один максимум, при z → ∞ fF (z) → 0, а при z ≤ 0 fF (z)=0. В табл.4П приложения содержатся правосторонние квантили плотности распределения случайной величины 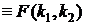 для различных значений степеней свободы, т.е. такие значения
для различных значений степеней свободы, т.е. такие значения 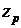 , при которых
, при которых 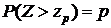 (р= 0,05).
(р= 0,05).

