Для каждой смешаннойстратегии 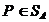 игрока
игрока 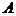 существует
существует 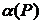
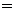
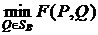 ;(4.1)
;(4.1)
Для каждой смешаннойстратегии 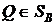 игрока
игрока 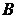 существует
существует 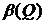
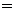
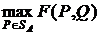 . (4.2)
. (4.2)
Доказательство:
Для проведения доказательства введём понятие симплекса
Стандартным n -симплексом называется подмножество пространства 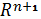 действительных чисел, определяемое как
действительных чисел, определяемое как
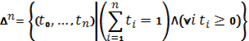 .
.
Его вершинами являются точки:
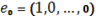 ,
,
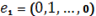 ,
,
…
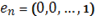 .
.
Сначала покажем, что симплекс является ограниченным замкнутым множеством, т.е. компактом.
Рассмотрим симплекс
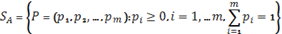
в евклидовом пространстве 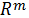 . Так как норма вектора
. Так как норма вектора 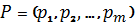 в пространстве
в пространстве 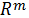 определяется следующим образом:
определяется следующим образом:
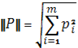 ,то для любой точки
,то для любой точки 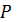 симплекса
симплекса 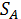 справедливо неравенство
справедливо неравенство
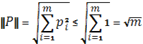 ,означающее ограниченность симплекса
,означающее ограниченность симплекса 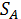 .
.
Пусть последовательность точек
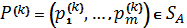 ,
, 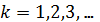 ,
,
сходится к точке 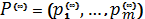 при
при 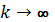 . Так как сходимость в
. Так как сходимость в 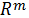 является покоординатной, то
является покоординатной, то 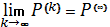 означает, что
означает, что 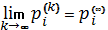 ,
, 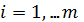 . Поскольку
. Поскольку  , то и
, то и 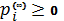 .
.
Так как 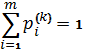 для каждого k, то
для каждого k, то
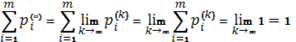 .
.
Таким образом, предельная точка 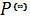 принадлежит симплексу
принадлежит симплексу 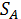 , что доказывает его замкнутость.
, что доказывает его замкнутость.
Аналогично и симплекс 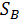 – компакт в пространстве
– компакт в пространстве 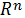 .
.
Если зафиксировать произвольную смешанную стратегию 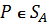 , то функция выигрыша
, то функция выигрыша 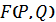 будет функцией одного векторного аргумента
будет функцией одного векторного аргумента 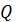 , определённой на симплексе
, определённой на симплексе 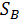 . Из аналитического выражения
. Из аналитического выражения
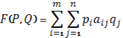 ,
, 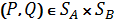
видно, что она непрерывна по аргументу Q на множестве 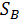 , которое, как мы только что установили, является компактом, а непрерывная на компакте функция достигает своей нижней и верхней граней. Поэтому для любого
, которое, как мы только что установили, является компактом, а непрерывная на компакте функция достигает своей нижней и верхней граней. Поэтому для любого 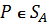 существует (4.1), т.е. для любого
существует (4.1), т.е. для любого 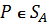 найдётся хотя бы одна точка
найдётся хотя бы одна точка 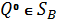 такая, что
такая, что
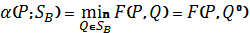 .
.
Аналогично доказывается и существование (4.2).
Теорема доказана.
13. Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.
Нижней ценой (или максимином) матричной игры в смешанных стратегия х называется величина 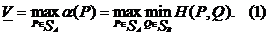
Верхней ценой (или минимаксом) матричной игры в смешанных стратегиях называется величина 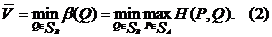
Докажем существование нижней и верхней цен в смешанных стратегиях, т.е. достижимость максимума в (1) и минимума в (2). Необходимость этого доказательства возникает по причине бесконечности множеств SA в (1) и SB в (2).
Сначала докажем вспомогательные предложения.
Лемма 1. Соответствие, сопоставляющее каждой смешанной стратегии Р 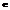 SA игрока А показатель ее эффективности α (Р),является числовой функцией, определенной на симплексе SA,аналитическое выражение которой задается равенством
SA игрока А показатель ее эффективности α (Р),является числовой функцией, определенной на симплексе SA,аналитическое выражение которой задается равенством
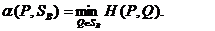
Аналогично, соответствие β (Q),задаваемое формулой 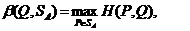
является числовой функцией, определенной на симплексе SB и ставящей в соответствие каждой смешанной стратегии Q 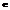 SB игрока В показатель ее неэффективности β (Q).
SB игрока В показатель ее неэффективности β (Q).
Доказательство. Для каждой смешанной стратегии P 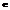 SA в силу теоремы 1 - для каждой смешанной (в частности, чистой) стратегии Р
SA в силу теоремы 1 - для каждой смешанной (в частности, чистой) стратегии Р 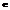 SA игрока А существует (достигается)
SA игрока А существует (достигается)
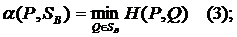
для каждой смешанной (в частности, чистой) стратегии Q 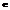 SB игрока В существует (достигается)
SB игрока В существует (достигается)
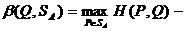 существует число
существует число 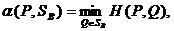 которое по определению минимума является единственным. Следовательно, α(Р)- числовая функция векторного аргумента Р, определенная на симплексе SA.
которое по определению минимума является единственным. Следовательно, α(Р)- числовая функция векторного аргумента Р, определенная на симплексе SA.
Аналогичной аргументацией обосновывается, что
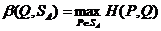 является числовой функцией векторного аргумента Q, определенного на симплексе SB.
является числовой функцией векторного аргумента Q, определенного на симплексе SB.
Лемма 2. Функции α (Р) и β (Q)непрерывны в своих областях определения SA и SB.
Оставим без доказательства. Теперь докажем следующую теорему.
Теорема 2. Для любой конечной матричной игры существуют нижняя и верхняя цены игры в смешанных стратегиях.Доказательство. Так как функция α (Р)по лемме 2 непрерывна на компакте SA, то она достигает на этом множестве своего максимума, т.е. существует нижняя цена игры в смешанных стратегиях: 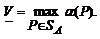
Аналогичным образом обосновывается существование и верхней цены игры в смешанных стратегиях:
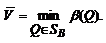
Смешанная стратегия PО 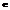 SA,максимизирующая показатель эффективности α (Р) (существование которой доказано в теореме 2), назовем максиминной смешанной стратегией игрока А. Таким образом, нижняя цена игры
SA,максимизирующая показатель эффективности α (Р) (существование которой доказано в теореме 2), назовем максиминной смешанной стратегией игрока А. Таким образом, нижняя цена игры 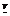 есть (см. 1) показатель эффективности максиминной смешанной стратегии PО:
есть (см. 1) показатель эффективности максиминной смешанной стратегии PО:
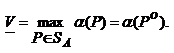
В частном случае PО =Аi0 является максиминной чистой стратегией игрока A.
Аналогично, смешанная стратегия QО 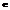 SB (существование которой доказано в теореме 2), минимизирующая показатель неэффективности β (Q), назовем минимаксной смешанной стратегией игрока В. Показатель неэффективности минимаксной смешанной стратегии QО равен верхней цене игры
SB (существование которой доказано в теореме 2), минимизирующая показатель неэффективности β (Q), назовем минимаксной смешанной стратегией игрока В. Показатель неэффективности минимаксной смешанной стратегии QО равен верхней цене игры 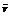 (см. 2)):
(см. 2)):
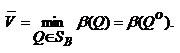
Если QО =Bj0, то Bj0является минимаксной чистой стратегией.
14.Теорема о соотношении нижней и верхней цен игры в чистых и смешанных стратегиях.
Теорема. Нижняя цена игры α и верхняя цена игры β в чистых стратегиях, нижняя цена игры 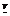 и верхняя цена игры
и верхняя цена игры 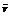 в смешанных стратегиях удовлетворяют следующим неравенствам:
в смешанных стратегиях удовлетворяют следующим неравенствам:
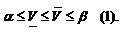
Доказательство. Начнем доказательство с левого неравенства (1).
По определению
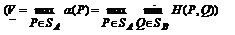
нижней цены в смешанных стратегиях 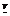
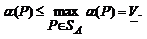
Здесь правая часть 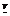 не зависит от Р и потому это неравенство остается верным и для Р = Ai, i = 1,..., m:
не зависит от Р и потому это неравенство остается верным и для Р = Ai, i = 1,..., m:
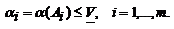
Так как полученное неравенство справедливо для всех i = 1,..., m, то оно будет справедливым в частности для того номера i,который максимизирует показатель эффективности αi:
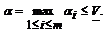
Итак, первое из неравенств (1) доказано.
Докажем второе неравенство 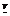 ≤
≤ 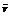 в (1). Для любых Р
в (1). Для любых Р 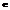 SA и Q
SA и Q 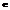 SB по
SB по
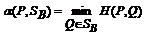 и
и 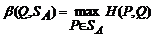
имеем:
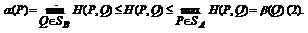
Соотношение (2) означает, что в любой ситуации в смешанных стратегиях (Р, Q)выигрыш H (P, Q)игрока A не меньше показателя эффективности α (P)его стратегии Р и не больше показателя неэффективности стратегии Q противника В.
Так как (2) справедливо для любых Р 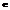 SA и Q
SA и Q 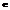 SB, то из него следует, что
SB, то из него следует, что
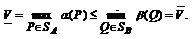
Докажем последнее (правое) из неравенств (1). В силу определения
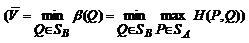
верхней цены игры в смешанных стратегиях
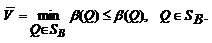
В частности, это неравенство справедливо и для чистых стратегий Q = Bj, j = 1,..., п,игрока В
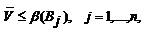
и, следовательно, неравенство остается в силе и для того номера j,который минимизирует показатель неэффективности β (Bj) стратегии Вj, т.е.
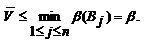
Итак, (1) доказано.
15. Основная теорема матричных игр Джона фон Неймана и седловая точка функции
Каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.
Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры: 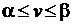 .
.
Применение первым игроком оптимальной стратегии 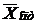 должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение
должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение
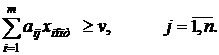
Аналогично для второго игрока оптимальная стратегия 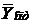 должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение
должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение
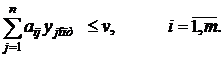
Если платежная матрица не содержит седловой точки, то задача определения смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому матрицы большой размерности целесообразно упростить, уменьшив их размерность путем вычеркивания дублирующих (одинаковых) и не доминирующих стратегий.
Если 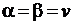 , то такая игра называется игрой с седловой точкой, элемент матрицы
, то такая игра называется игрой с седловой точкой, элемент матрицы 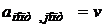 , соответствующий паре оптимальных стратегий
, соответствующий паре оптимальных стратегий 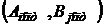 называется седловой точкой матрицы. Этот элемент является ценой игры.
называется седловой точкой матрицы. Этот элемент является ценой игры.
16.Аналитическое решение игры 2×2 в смешанных стратегиях.
Рассмотрим игру 2х2.
Если такая игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке. Для игры, в которой отсутствует седловая точка оптимальное решение игры существует и определяется парой смешанных стратегий (x1*,x*2) и (у1*,у2*).
(!!!это заменяем на следующее обозначение смешанных стратегий P0 =(p10;p20) andQ=(q10;q20), соответственно дальше меняем сами)
2) Для того, чтобы их найти, воспользуемся теоремой об активных стратегиях.
 Если первый игрок придерживается своей оптимальной смешанной стратегии, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией не пользовался второй игрок. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Поэтому средний выигрыш и первого и второго игрока будет равен цене игры.
Если первый игрок придерживается своей оптимальной смешанной стратегии, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией не пользовался второй игрок. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Поэтому средний выигрыш и первого и второго игрока будет равен цене игры.
3) Пусть игра задана матрицей
Средний выигрыш первого игрока, если он использует оптимальную смешанную стратегию х*=(x1*,x*2), а второй игрок – чистую стратегию, соответ.первому столбцу платежной матрицы, равен цене игры v:
a11x1*+a21x*2 = v.
Тот же средний выигрыш получает первый игрок, если второй игрок применяет стратегию, соответ.второму столбцу платежной матрицы, т.е. a12x1*+a22x*2 = v. Учитывая, что x1*+ x*2=1, получаем систему уравнений для определения оптимальной стратегии первого игрока и цены игры:
a11 x1*+a21 x*2 = v.
a12 x1*+a22 x*2 = v
x1*+ x*2=1
Решая эту систему, получим оптимальную стратегию
x1*= 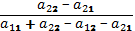
x2*= 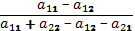
и цену игры v = 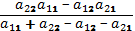
4) 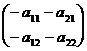 Для второго игрока
Для второго игрока
В=-АТ=
Применяя теорему об активных стратегиях при отыскании оптимальной смешанной стратегии второго игрока, получаем, что при любой чистой стратегии первого игрока средний проигрыш второго игрока равен v, т.е. a11 у1*+ a12 у2*=v.
Тогда оптимальная стратегия второго игрока определяется по формулам:
у1*= 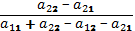
у2*= 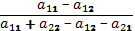
v’=-v
17. Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока A.
Итак, мы можем сформулировать общий алгоритм геометрического нахождения оптимальных стратегий игрока А, цены игры, нижней и верхней цены игры в чистых стратегиях, седловых точек матрицы и доминирующих стратегий игроков.
1. Берем горизонтальный отрезок [0,1].
2. В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый соответ. стратегии А1 и правый, соотв.стратегии А2.
3. На левом перпендикуляре от точки 0 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) элементы a11 и a12 первой строки матрицы А
4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] (как на вертикальной числовой оси) элементы a21 и a22 второй строки матрицы А
5. Соединяем точки, изображающие элементы с одинаковыми вторыми индексами, т.е. эл-ты, стоящие в одном и том же столбце матрицы А: a11 с a21 и a12 с a22. В результате получаем отрезки a11a21 и a12a22.
6. Если отрезки a11a21 и a12a22 не убывающие, то стратегия А2 доминирует стратегию А1. Если отрезки a11a21 и a12a22 возрастающие, то стратегия А2 строго доминирует А1.
7. Если отрезок a11a21 лежит не ниже отрезка a12a22, то стратегия В2 доминирует стратегию В1. Если отрезок a11a21 лежит выше отрезка a12a22 и не пересекается с ним, то стратегия В2 строго доминирует стратегию В1
8. Находим нижнюю огибающую отрезков a11a21 и a12a22
9. Находим наивысшие точки нижней огибающей
10. Проектируем их ортогонально на горизонтальный отрезок [0,1]
11. Полученные проекции р0 определяют оптимальные стратегии Р0=(1-р0,р0) игрока А.
12. Ордината наивысшей точки огибающей равна цене игры V
13. Верхний из двух концов нижней огибающей (лежащих на перпендикулярах) есть нижняя цена игры в чистых стратегиях 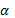
14. Нижний из двух верхних концов отрезков a11a21 и a12a22 есть верхняя цена игры в чистых стратегиях 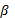
15. Если элемент является нижним на перпендикуляре, где он лежит, и верхним концом отрезка a11a21 или a12a22, на котором он лежит, то этот эл-т является седловой точкой. В этом случае чистая стратегия игрока В, номер которой совпадает со вторым индексом седловой точки, является оптимальной.
Мы дали геометрическую интерпретацию оптимальных стратегий игрока А. Если матрица игры содержит седловую точку, то автоматически выявляется и оптимальная стратегия игрока В. Но можно достаточно удовлетворительно проинтерпретировать геометрически оптимальную стратегию игрока В и в случае отсутствия седловых точек.
18. Геометрический метод нахождения цены игры 2×2 и оптимальных стратегий игрока B.
1. Берем горизонтальный отрезок [0,1].
2. В концах отрезка [0,1] проводим к нему 2 перпендикуляра: левый и правый
3. На левом перпендикуляре вертикальной числовой оси от точки 0 его пересечения с отрезком [0,1] откладываем все элементы матрицы А, за исключением а22
4. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все эл-ты матрицы А, за исключением а11
5. Каждый элемент на левом перпендикуляре соединим отрезком с каждым элементом на правом перпендикуляре, отличающимся от него только одним индексом. В результате получим отрезки a11a21, a12a22, a11a12 и a21a22
6. Находим нижнюю огибающую отрезов a11a21 и a12a22.
7. Находим аивысшую точку N нижней огибающей.
8. Находим абсциссу р0 наивысшей точки нижней огибающей.
9. Смешанная стратегия Р0=(1-р0, р0) является оптимальной стратегией игрока А.
10. Находим верхнюю огибающую отрезков a11a12 и a21a22.
11. Находим наинизшую точку М верхней огибающей.
12. Находим абсциссу q0 наинизшей точки верхней огибающей.
13. Смешанная стратегия Q0=(1-q0,q0) является оптимальной стратегией игрока В.
14. Ордината наивысшей точки нижней огибающей равна ординате наинизшей точки верхней огибающей и представляет собой цену игры V.
15. Т.о. найдено геометрическими средствами решение игры {P0,Q0,V}
16. Верхний из концов нижней огибающей (лежащей на перпендикулярах) есть нижняя цена игры в чистых стратегиях 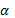
17. Нижний из концов верхней огибающей (лежащий на перпендикулярах) есть верхняя цена игры в чистых стратегиях 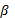
19.Геометрический метод нахождения цены игры 2× n и оптимальных стратегий игрока A.
20. Геометрический метод нахождения цены игры m×2 и оптимальных стратегий игрока B.
(!!! Помним про обозначения вероятностей чистых стратегий через p,q)
Решение игр размера 2xn или nx2 допускает наглядную геометрическую интерпретацию. Такие игры можно решать графически.
1) Дадим геометрическую интерпретацию игры
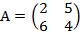
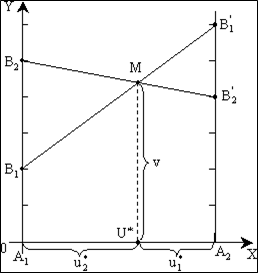
На плоскости XY по оси абсцисс отложим единичный отрезок A1A2 (рисунок 5.1). Каждой точке отрезка поставим в соответствие некоторую смешанную стратегию U = (u1, u2). Причем расстояние от некоторой промежуточной точки U до правого конца этого отрезка – это вероятность u1 выбора стратегии A1, расстояние до левого конца - вероятность u2 выбора стратегии A2. Точка А1 соответствует чистой стратегии А1, точка А2 – чистой стратегии А2.
В точках А1 и А2 восстановим перпендикуляры и будем откладывать на них выигрыши игроков. На первом перпендикуляре (совпадающем с осью OY) покажем выигрыш игрока А при использовании стратегии А1, на втором – при использовании стратегии A2. Если игрок А применяет стратегию A1, то его выигрыш при стратегии B1 игрока B равен 2, а при стратегии B2 он равен 5. Числам 2 и 5 на оси OY соответствуют точки B1 и B2. Аналогично на втором перпендикуляре найдем точки B'1 и B'2 (выигрыши 6 и 4).
Соединяя между собой точки B1 и B'1, B2 и B'2, получим две прямые, расстояние от которых до оси OX определяет средний выигрыш при любом сочетании соответствующих стратегий.
Например, расстояние от любой точки отрезка B1B'1 до оси OX определяет средний выигрыш игрока A при любом сочетании стратегий A1 и A2 (с вероятностями u1 и u2) и стратегии B1 игрока B.
Рисунок 5.1 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока А)
Ординаты точек, принадлежащих ломаной B1MB'2 определяют минимальный выигрыш игрока A при использовании им любых смешанных стратегий. Эта минимальная величина является наибольшей в точке М, следовательно, этой точке соответствует оптимальная стратегия U* = (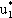 ,
, 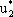 ), а ее ордината равна цене игры v.
), а ее ордината равна цене игры v.
Координаты точки M найдем, как координаты точки пересечения прямых B1B'1 и B2B'2.
Для этого необходимо знать уравнения прямых. Составить такие уравнения можно, используя формулу для уравнения прямой, проходящей через две точки:
Составим уравнения прямых для нашей задачи.
Прямая B1B'1:
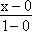 = = 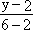 или y = 4x + 2. или y = 4x + 2.
|
Прямая B2B'2:
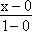 = = 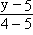 или y = -x + 5. или y = -x + 5.
|
Получим систему:
| y = 4x + 2, y = -x + 5.
|
|
|
Решим ее:
|
| 4x + 2 = -x + 5, 5x = 3, x = 3/5, y = -3/5 + 5 = 22/5.
|
Таким образом, U* = (2/5, 3/5), v = 22/5.
Аналогично решается задача по нахождению оптимальной стратегии игрока B. Разница состоит в том, что находится точка, сводящая к минимуму средний проигрыш, поэтому на рисунке 5.2 рассматривается ломаная A2MA'1.
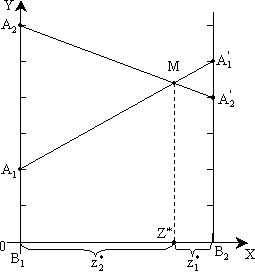 Рисунок 5.2 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока B)
Рисунок 5.2 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока B)
Найдем координаты точки М.
Прямая A1A'1:
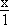 = = 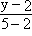 , откуда y = 3x + 2. , откуда y = 3x + 2.
|
Прямая A2A'2:
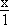 = = 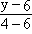 , откуда y = -2x + 6, , откуда y = -2x + 6,
|
|
| 3x + 2 = -2x + 6, 5x = 4, x = 4/5.
|
Таким образом, 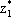 = 1/5,
= 1/5, 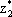 = 4/5.
= 4/5.



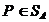 игрока
игрока 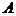 существует
существует 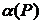
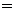
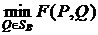 ;(4.1)
;(4.1)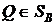 игрока
игрока 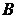 существует
существует 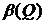
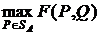 . (4.2)
. (4.2)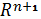 действительных чисел, определяемое как
действительных чисел, определяемое как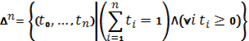 .
.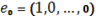 ,
,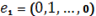 ,
,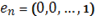 .
.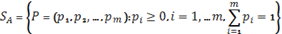
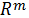 . Так как норма вектора
. Так как норма вектора 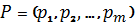 в пространстве
в пространстве 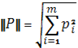 ,то для любой точки
,то для любой точки 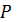 симплекса
симплекса 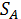 справедливо неравенство
справедливо неравенство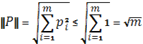 ,означающее ограниченность симплекса
,означающее ограниченность симплекса 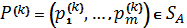 ,
, 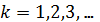 ,
,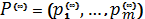 при
при 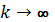 . Так как сходимость в
. Так как сходимость в 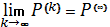 означает, что
означает, что 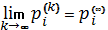 ,
, 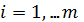 . Поскольку
. Поскольку  , то и
, то и 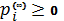 .
.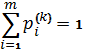 для каждого k, то
для каждого k, то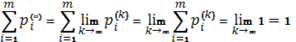 .
.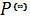 принадлежит симплексу
принадлежит симплексу 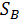 – компакт в пространстве
– компакт в пространстве 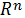 .
.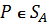 , то функция выигрыша
, то функция выигрыша 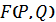 будет функцией одного векторного аргумента
будет функцией одного векторного аргумента 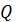 , определённой на симплексе
, определённой на симплексе 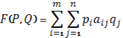 ,
, 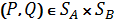
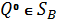 такая, что
такая, что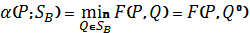 .
.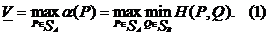
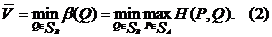
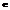 SA игрока А показатель ее эффективности α (Р),является числовой функцией, определенной на симплексе SA,аналитическое выражение которой задается равенством
SA игрока А показатель ее эффективности α (Р),является числовой функцией, определенной на симплексе SA,аналитическое выражение которой задается равенством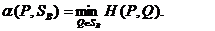
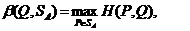
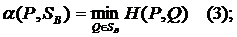
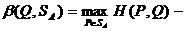 существует число
существует число 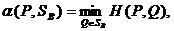 которое по определению минимума является единственным. Следовательно, α(Р)- числовая функция векторного аргумента Р, определенная на симплексе SA.
которое по определению минимума является единственным. Следовательно, α(Р)- числовая функция векторного аргумента Р, определенная на симплексе SA.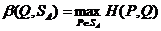 является числовой функцией векторного аргумента Q, определенного на симплексе SB.
является числовой функцией векторного аргумента Q, определенного на симплексе SB.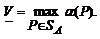
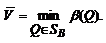
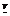 есть (см. 1) показатель эффективности максиминной смешанной стратегии PО:
есть (см. 1) показатель эффективности максиминной смешанной стратегии PО: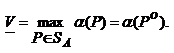
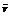 (см. 2)):
(см. 2)):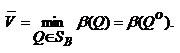
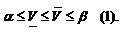
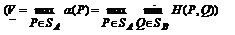
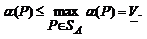
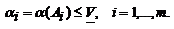
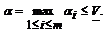
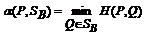 и
и 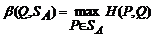
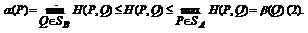
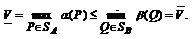
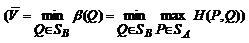
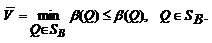
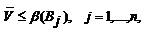
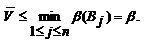
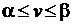 .
.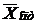 должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение
должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры. Поэтому выполняется соотношение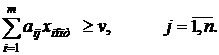
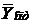 должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение
должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры, т.е. справедливо соотношение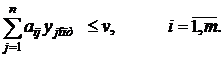
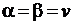 , то такая игра называется игрой с седловой точкой, элемент матрицы
, то такая игра называется игрой с седловой точкой, элемент матрицы 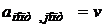 , соответствующий паре оптимальных стратегий
, соответствующий паре оптимальных стратегий 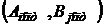 называется седловой точкой матрицы. Этот элемент является ценой игры.
называется седловой точкой матрицы. Этот элемент является ценой игры. Если первый игрок придерживается своей оптимальной смешанной стратегии, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией не пользовался второй игрок. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Поэтому средний выигрыш и первого и второго игрока будет равен цене игры.
Если первый игрок придерживается своей оптимальной смешанной стратегии, то его средний выигрыш будет равен цене игры v, какой бы активной стратегией не пользовался второй игрок. Для игры 2х2 любая чистая стратегия противника является активной, если отсутствует седловая точка. Поэтому средний выигрыш и первого и второго игрока будет равен цене игры.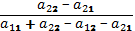
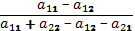
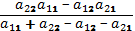
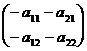 Для второго игрока
Для второго игрока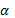
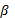

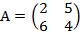
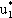 ,
, 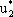 ), а ее ордината равна цене игры v.
), а ее ордината равна цене игры v.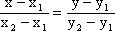
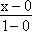 =
= 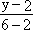 или y = 4x + 2.
или y = 4x + 2.
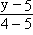 или y = -x + 5.
или y = -x + 5.
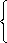
 Рисунок 5.2 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока B)
Рисунок 5.2 – Геометрическая интерпретация игры примера 5.3 (нахождение оптимальной стратегии игрока B)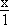 =
= 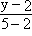 , откуда y = 3x + 2.
, откуда y = 3x + 2.
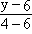 , откуда y = -2x + 6,
, откуда y = -2x + 6,
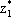 = 1/5,
= 1/5, 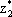 = 4/5.
= 4/5.

