Пусть  .
.
Тогда  . Здесь t(x) – дифференцируемая монотонная функция.
. Здесь t(x) – дифференцируемая монотонная функция.
При решении задач замену переменной можно выполнить двумя способами.
1. Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и 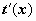 , то замена переменной осуществляется подведением множителя
, то замена переменной осуществляется подведением множителя 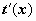 под знак дифференциала:
под знак дифференциала:  , и задача сводится к вычислению интеграла
, и задача сводится к вычислению интеграла  . Например,
. Например,  (задача сведена к вычислению
(задача сведена к вычислению  , где t = cosx)
, где t = cosx)  (аналогично находится интеграл от
(аналогично находится интеграл от  );
); 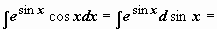 (задача сведена к вычислению
(задача сведена к вычислению  , где t = sin x)
, где t = sin x)  .
.
2. Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной.
Пример 1. 
Имеет смысл перейти к переменной (сделать подстановку) t = sin x. Выражаем все множители подынтегрального выражения через переменную t: 
в результате:


(возвращаемся к исходной переменной)
 .
.
Пример 2. 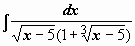 .
.
Подынтегральная функция содержит два множителя, ни один из которых не является производной другого, поэтому подводить их под знак дифференциала бесполезно. Попытаемся ввести новую переменную, такую, чтобы корни извлеклись:
 =
= 
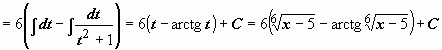
Пример 3.  (интеграл №19 из табл.).
(интеграл №19 из табл.).
Здесь подынтегральная функция состоит из единственного множителя; можно опять попытаться сделать такую замену переменной, чтобы корень извлёкся. Структура подкоренного выражения подсказывает эту замену:  (или
(или  ,
, 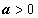 ):
):
 .
.
Интеграл свёлся к интегралу от квадрата косинуса. При интегрировании чётных степеней синуса и косинуса часто применяются формулы, выражающие  и
и  через косинус двойного угла:
через косинус двойного угла:  .
.
Поэтому 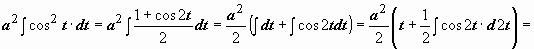
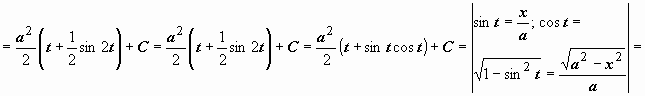
 .
.
Пример 4.
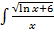 dx=
dx=  =
=  dt=
dt= 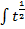 dt=
dt=  +С=
+С= 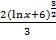 +С
+С
Интегрирование по частям
Производится по формуле: 
Пример 5.
 =
=  =
=
=x·  =x·
=x· 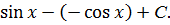
Пример 6.
 =
=  =
=
=  =
= 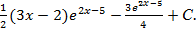
Пример 7.
 =
=  =
=
= 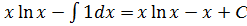 .
.
Определенный интеграл, его свойства и вычисление
Определенный интеграл вычисляется по формуле Ньютона-Лейбница:
 = F(a)-F(b)
= F(a)-F(b)
 – соответственноверхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
– соответственноверхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
Основные свойства определенного интеграла:
1. При перестановке пределов интегрирования изменяется знак интеграла:

2. Отрезок интегрирования можно разбивать на части:

3. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов.
4. Постоянный множитель можно выносить за знак интеграла.
Пример 1.
 =
= 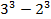 =27-8=19.
=27-8=19.
Вычисления определённого интеграла методом введения новой переменной

Пример 2.
 =
=
=  =
=  =
= 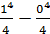 =
= 
Пример 3.
 = -
= -  =
=
=-  (
( )=-
)=- 
Вычисление определенного интеграла по частям
Используем формулу:
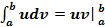 -
- 
Пример 4.
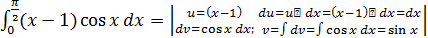 =
=
 -
-  +
+  =
=
=( )+
)+  -1-1=
-1-1=  -2;
-2;
Пример 5.
 =-6xctgx
=-6xctgx  +
+  =
=
=-6· 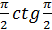 -6·
-6·  +ln|sinx|
+ln|sinx| 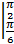 =π
=π  + ln|sin
+ ln|sin  |- ln|sin
|- ln|sin  |=
|=
= π  + ln1- ln
+ ln1- ln  = π
= π  + 0+ln2= π
+ 0+ln2= π  +ln2
+ln2
Нахождение площадей фигур
Криволинейной трапецией называется плоская фигура, ограниченная осью
 , прямыми
, прямыми  ,
, 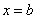 и графиком непрерывной на отрезке
и графиком непрерывной на отрезке  функции
функции  , которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:
, которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:

Тогда площадь криволинейной трапеции численно равна определенному интегралу  .
.
Определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры.
Пример 1. Вычислить площадь фигуры, ограниченной линиями  ,
, 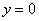 ,
,
 ,
,  .
.
Это типовая формулировка задания. Первый и важнейший момент решения – построение чертежа.
Выполним чертеж (обратите внимание, что уравнение 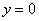 задает ось
задает ось  ):
):
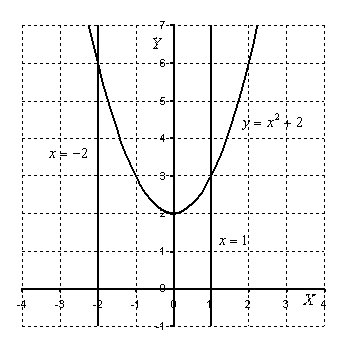
О какой площади идет речь, очевидно. Решение продолжается так:
На отрезке  график функции
график функции  расположен над осью
расположен над осью  , поэтому:
, поэтому:

Ответ: 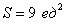
После того, как задание выполнено, всегда полезно взглянуть на чертеж и прикинуть, реальный ли получился ответ.
Пример 2. Вычислить площадь фигуры, ограниченной линиями 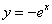 ,
,  и координатными осями.
и координатными осями.
Решение: Выполним чертеж:

Если криволинейная трапеция расположена под осью  (или, по крайней мере, не выше данной оси), то её площадь можно найти по формуле:
(или, по крайней мере, не выше данной оси), то её площадь можно найти по формуле:

В данном случае:

Ответ: 
Внимание! Не следует путать два типа задач:
1) Если Вам предложено решить просто определенный интеграл без всякого геометрического смысла, то он может быть отрицательным.
2) Если Вам предложено найти площадь фигуры с помощью определенного интеграла, то площадь всегда положительна! Именно поэтому в только что рассмотренной формуле фигурирует минус.
Пример 3. Найти площадь плоской фигуры, ограниченной линиями
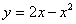 ,
,  .
.
Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы 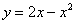 и прямой
и прямой  . Это можно сделать решив уравнение или построив линии поточечно. Решим уравнение:
. Это можно сделать решив уравнение или построив линии поточечно. Решим уравнение:

Значит, нижний предел интегрирования  , верхний предел интегрирования
, верхний предел интегрирования  .
.
Возвращаемся к нашей задаче: рациональнее сначала построить прямую и только потом параболу. Выполним чертеж:

А теперь рабочая формула: Если на отрезке  некоторая непрерывная функция
некоторая непрерывная функция  больше либо равна некоторой непрерывной функции
больше либо равна некоторой непрерывной функции  , то площадь фигуры, ограниченной графиками данных функций и прямыми
, то площадь фигуры, ограниченной графиками данных функций и прямыми  ,
, 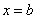 , можно найти по формуле:
, можно найти по формуле: 
Здесь уже не надо думать, где расположена фигура – над осью или под осью, и, грубо говоря, важно, какой график ВЫШЕ (относительно другого графика), а какой – НИЖЕ.
В рассматриваемом примере, очевидно, что на отрезке  парабола располагается выше прямой, а поэтому из
парабола располагается выше прямой, а поэтому из 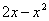 необходимо вычесть
необходимо вычесть 
Искомая фигура ограничена параболой 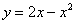 сверху и прямой
сверху и прямой  снизу.
снизу.
На отрезке 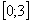
 , по соответствующей формуле:
, по соответствующей формуле: 
Ответ: 
Пример 4. Вычислить площадь фигуры, ограниченной линиями  ,
,
 ,
, 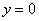 ,
,  .
.
Решение: Сначала выполним чертеж:

Фигура, площадь которой нам нужно найти, представлена крупной штриховкой (внимательно смотрите на условие – чем ограничена фигура!).
Этот пример еще полезен и тем, что в нём площадь фигуры считается с помощью двух определенных интегралов. Действительно:
1) На отрезке  над осью
над осью  расположен график прямой
расположен график прямой  ;
;
2) На отрезке  над осью
над осью  расположен график гиперболы
расположен график гиперболы  .
.
Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:

Ответ: 
Пример 5. Вычислить площадь фигуры, ограниченной линиями
 ,
, 
Представим уравнения в явном виде  ,
,  и выполним поточечный чертеж:
и выполним поточечный чертеж:

Из чертежа видно, что верхний предел у нас «хороший»: 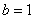 .
.
Но чему равен нижний предел?! Понятно, что это не целое число, но какое? Может быть  ? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что
? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что 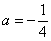 . Или корень. А если мы вообще неправильно построили график?
. Или корень. А если мы вообще неправильно построили график?
В таких случаях приходиться тратить дополнительное время и уточнять пределы интегрирования аналитически.
Найдем точки пересечения прямой  и параболы
и параболы  .
.
Для этого решаем уравнение:


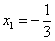 ,
, 
Действительно,  .
.
На отрезке 
 , по соответствующей формуле:
, по соответствующей формуле:
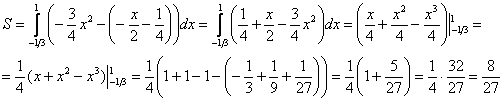
Ответ: 
Пример 6. Вычислить площадь фигуры, ограниченной линиями
 ,
, 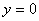 ,
, 
Решение: Изобразим данную фигуру на чертеже.

С пределами интегрирования здесь проблем нет, они следуют прямо из условия:  – «икс» изменяется от нуля до «пи». Оформляем дальнейшее решение:
– «икс» изменяется от нуля до «пи». Оформляем дальнейшее решение:
На отрезке  график функции
график функции  расположен над осью
расположен над осью  , поэтому:
, поэтому:
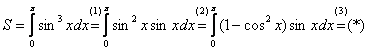
Используем основное тригонометрическое тождество в виде 
Проведем замену переменной  , тогда:
, тогда:

Новые пределы интегрирования:
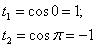
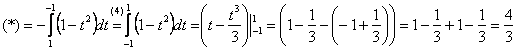
(4) Здесь мы использовали свойство определенного интеграла  , расположив пределы интегрирования в «привычном» порядке
, расположив пределы интегрирования в «привычном» порядке
Ответ: 
Использованные источники:
1. http://mathprofi.ru/
2. http://www.webmath.ru/



 .
. . Здесь t(x) – дифференцируемая монотонная функция.
. Здесь t(x) – дифференцируемая монотонная функция.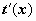 , то замена переменной осуществляется подведением множителя
, то замена переменной осуществляется подведением множителя  , и задача сводится к вычислению интеграла
, и задача сводится к вычислению интеграла  . Например,
. Например,  (задача сведена к вычислению
(задача сведена к вычислению  , где t = cosx)
, где t = cosx)  (аналогично находится интеграл от
(аналогично находится интеграл от  );
); 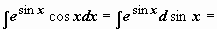 (задача сведена к вычислению
(задача сведена к вычислению  , где t = sin x)
, где t = sin x)  .
.



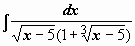 .
. =
= 
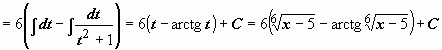
 (интеграл №19 из табл.).
(интеграл №19 из табл.). (или
(или  ,
, 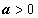 ):
):  .
. и
и  через косинус двойного угла:
через косинус двойного угла:  .
.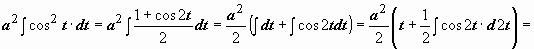
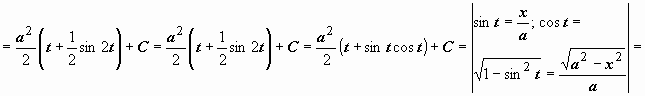
 .
.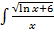 dx=
dx=  =
=  dt=
dt= 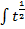 dt=
dt=  +С=
+С= 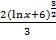 +С
+С
 =
=  =
= =x·
=x· 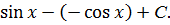
 =
=  =
= =
= 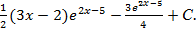
 =
=  =
=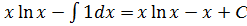 .
. = F(a)-F(b)
= F(a)-F(b) – соответственноверхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)
– соответственноверхний и нижний пределы интегрирования, они пишутся и читаются снизу вверх, а в формулу подставляются сверху вниз!)

 =
= 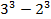 =27-8=19.
=27-8=19.
 =
= =
=  =
= 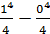 =
= 
 = -
= -  =
= (
( )=-
)=- 
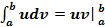 -
- 
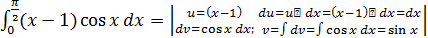 =
= -
-  +
+  =
= )+
)+  -1-1=
-1-1=  -2;
-2; =-6xctgx
=-6xctgx  +
+  =
=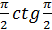 -6·
-6·  +ln|sinx|
+ln|sinx| 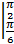 =π
=π  + ln|sin
+ ln|sin  |=
|= = π
= π  , прямыми
, прямыми  ,
, 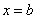 и графиком непрерывной на отрезке
и графиком непрерывной на отрезке  функции
функции  , которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:
, которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс:
 .
. ,
, 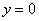 ,
,  ,
,  .
.
 график функции
график функции 
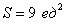
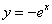 ,
, 



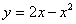 ,
,  .
.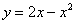 и прямой
и прямой 
 , верхний предел интегрирования
, верхний предел интегрирования  .
.
 больше либо равна некоторой непрерывной функции
больше либо равна некоторой непрерывной функции  , то площадь фигуры, ограниченной графиками данных функций и прямыми
, то площадь фигуры, ограниченной графиками данных функций и прямыми 
 парабола располагается выше прямой, а поэтому из
парабола располагается выше прямой, а поэтому из 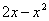 необходимо вычесть
необходимо вычесть 
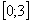
 , по соответствующей формуле:
, по соответствующей формуле: 

 ,
, ,
,  .
.
 над осью
над осью  над осью
над осью 

 ,
, 
 ,
,  и выполним поточечный чертеж:
и выполним поточечный чертеж:
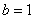 .
. ? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что
? Но где гарантия, что чертеж выполнен с идеальной точностью, вполне может оказаться что 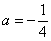 . Или корень. А если мы вообще неправильно построили график?
. Или корень. А если мы вообще неправильно построили график?

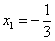 ,
, 

 , по соответствующей формуле:
, по соответствующей формуле: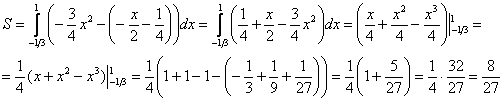

 ,
, 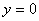 ,
, 

 график функции
график функции  расположен над осью
расположен над осью 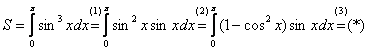

 , тогда:
, тогда:
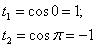
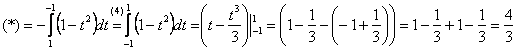
 , расположив пределы интегрирования в «привычном» порядке
, расположив пределы интегрирования в «привычном» порядке



