

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
Топ:
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Задана случайная величина Х: х 1, х 2, …, хn, так как М (Х) не найти, то для математического ожидания случайной величины Х естественно предложить среднее арифметическое
 (1.3)
(1.3)
её наблюденных значений.
1. По методу произведений
 ,
,  ,
,
так как
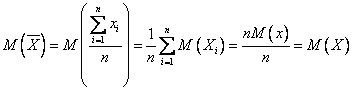 .
.
Это и означает, что оценка 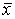 несмещенная.
несмещенная.
2. Если исследуемая случайная величина Х имеет конечную дисперсию, то эта оценка будет состоятельной, так как
 .
.
Если исследуемая величина имеет нормальный закон распределения, то можно показать, что предложенная оценка эффективна, т. е. оценки для математического ожидания с меньшей дисперсией не существует для нормально распределенных величин.
Точечная оценка математического ожидания
Пусть  выборка из генеральной совокупности, соответствующей случайной величине x с неизвестным математическим ожиданием Mx =q и известной дисперсией
выборка из генеральной совокупности, соответствующей случайной величине x с неизвестным математическим ожиданием Mx =q и известной дисперсией  .
.
Рассмотрим оценку неизвестного математического ожидания
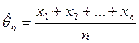 .
.
Оценка несмещённая, поскольку её математическое ожидание равно Mx =q:
 ,
,
Оценка состоятельная, поскольку при n® ¥,  :
:
 .
.
Итак, для оценки неизвестного математического ожидания случайной величины будем использовать выборочное среднее:  .
.
Точечная оценка для дисперсии
Так как дисперсия определяется через математическое ожидание, а для математического ожидания оценка уже выбрана, то для дисперсии естественно предложить оценку:
 или
или  ; (1.4)
; (1.4)
 , (1.5)
, (1.5)
что соответствует записи дисперсии в виде  .
.
Оказывается, что предложенная оценка дисперсии (1.4) состоятельна (легко доказать) и (1.5) не является несмещенной. Чтобы в этом убедиться, возведём в квадрат последнее слагаемое в (1.4)

Процентрируем величину Х, т. е. перенесем начало координат в точку М (Х):  . Дисперсия зависит лишь от разности значений Х и математического ожидания, поэтому от переноса начала координат оценка не изменится и равенство можно продолжить:
. Дисперсия зависит лишь от разности значений Х и математического ожидания, поэтому от переноса начала координат оценка не изменится и равенство можно продолжить:
|
|
 .
.
Вычислим теперь математическое ожидание полученной величины
 ,
,
т. е.  , так как
, так как 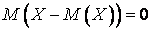 .
.
Значит, предложенная оценка занижает истинное значение дисперсии.
Для получения несмещенной оценки введем поправку и полученную оценку обозначим через S 2
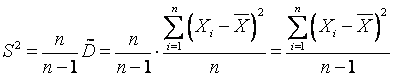
или
 . (1.6)
. (1.6)
Оценка S 2 (1.6) является состоятельной, так как  сходится по вероятности к М(Х 2 ), а
сходится по вероятности к М(Х 2 ), а  – к М(Х).
– к М(Х).
Замечание. При малых n дробь  довольно значительно отличается от единицы, а с увеличением n стремится к единице. При n > 50 практически нет разницы между оценками
довольно значительно отличается от единицы, а с увеличением n стремится к единице. При n > 50 практически нет разницы между оценками  и S2. Оценки
и S2. Оценки  и S2 являются состоятельными оценками дисперсии.
и S2 являются состоятельными оценками дисперсии.
Для дисперсии  случайной величины
случайной величины  можно предложить следующую оценку:
можно предложить следующую оценку:
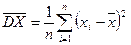 , где
, где  — выборочное среднее.
— выборочное среднее.
Доказано, что эта оценка состоятельная, но смещенная.
В качестве состоятельной несмещенной оценки дисперсии используют величину
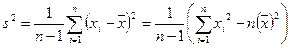 .
.
Именно несмещенностью оценки  объясняется ее более частое использование в качестве оценки дисперсии.
объясняется ее более частое использование в качестве оценки дисперсии.
|
|
|

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!