2) Если ко всем вариантам добавить постоянное число, то дисперсия не изменится.
3) Если все варианты умножить на одно и то же число  , то дисперсия умножится на
, то дисперсия умножится на  .
.
Рассмотрим основные свойства выборочной дисперсии, считая при этом, что наблюдаемые.данные представлены в виде дискретного вариационного ряда.
1°. Дисперсия постоянной величины равна нулю
2°. Если все результаты наблюдений увеличить (уменьшить) на одно и то же число С, то дисперсия и среднее квадратическое отклонение не изменятся
3°. Если все результаты наблюдений умножить на одно и то же число, то имеет место равенство Ď(СХ)=С²ĎХ
4°. Если все частоты вариантов умножить на одно и то же число, то выборочные дисперсия и среднее квадратическое отклонение не изменятся.
5°. Выборочная дисперсия равна разности между средним арифметическим квадратов наблюдений над случайной величиной и квадратом ее среднего арифметического, т. е.
ĎХ=˜Х²-(˜Х)²
Определение. Размахом вариации называется число R=хmax – xmin.
Мерой вариации признака является выборочное среднее квадратическое отклонение, которое определяется как корень из дисперсии:
 (4)
(4)
46. Начальным выборочным моментом k -го порядка называется величина, определяемая по формуле:
 ,
,
где хi – наблюдаемое значение с частотой ni, n – число наблюдений. В частности, начальный выборочный момент первого порядка обозначается  и называется выборочной средней:
и называется выборочной средней:
 .
.
Медианой называется значение признака, приходящееся на середину ранжированного ряда наблюдений.
Модой называется вариант, которому соответствует наибольшая частота.
Вариационный размах R равен разности между наибольшим и наименьшим вариантом ряда.
Центральным выборочным моментом k-го порядка называется величина, определяемая по формуле:
 .
.
В частности, центральной выборочный момент второго порядка обозначается S 2 и называется выборочной дисперсией:
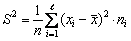 .
.
Средним квадратическим отклонением S называется арифметическое значение корня квадратного из дисперсии:
 .
.
Коэффициентом вариации называется отношение среднего квадратического отклонения к средней, выраженное в процентах:
 .
.
Справедливы следующие формулы, выражающие центральные выборочные моменты различных порядков через начальные:

 и т.д.
и т.д.
Выборочным коэффициентом асимметрии называется число  , определяемое формулой
, определяемое формулой
 .
.
Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона (см. далее) вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.
В случае отрицательного коэффициента асимметрии более пологий «спуск» полигона наблюдается слева, в противном случае – справа. В первом случае асимметрию называют левосторонней, а во втором – правосторонней.
Выборочным эксцессом или коэффициентом крутизны называется число E˜k, определяемое формулой
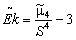 .
.
Выборочный эксцесс служит для сравнения на «крутость» выборочного распределения с нормальным распределением. Ранее подчеркивалось, что эксцесс для случайной величины, распределенной нормально, равен нулю. Поэтому за стандартное значение выборочного эксцесса принимают E˜k = 0. Если выборочному распределению соответствует отрицательный эксцесс, то соответствующий полигон имеет более пологую вершину по сравнению с нормальной кривой. В случае положительного эксцесса полигон более крутой по сравнению с нормальной кривой.
47. Точечное оценивание параметра генерального распределения — это нахождение его точечной оценки, т.е. такого значения некоторой выборочной статистики (см. п. 3), о котором можно говорить как о хорошем приближении к неизвестному генеральному значению параметра. Точечные выборочные оценки должны быть несмещенными (среднее выборочного распределения оценки (см. Статистика, п. 3) должно быть равно величине оцениваемого генерального параметра), состоятельными (при росте объема выборок значение статистики должно приближаться к значению генерального параметра) и эффективными (разброс выборочного распределения статистики должен быть как можно меньше, эффективность — относительная величина). Выполнение этих условий снижает вероятность того, что выборочная точечная оценка окажется далекой от значений соответствующего параметра изучаемого генерального распределения.
Для примера заметим, что выборочное среднее арифметическое при любом виде генерального распределения является несмещенной, состоятельной, эффективной оценкой генерального математического ожидания. Для симметричного распределения несмещенной и состоятельной оценкой математического ожидания является и медиана, а для симметричного и унимодального — мода. Однако и медиана, и мода — менее эффективные оценки, чем среднее арифметическое: последнее в меньшей степени варьируется от выборки к выборке, чем мода и медиана. Поэтому мода и медиана не используются для оценки математического ожидания.



 , то дисперсия умножится на
, то дисперсия умножится на  .
. (4)
(4) ,
, и называется выборочной средней:
и называется выборочной средней: .
. .
.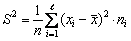 .
. .
. .
.
 и т.д.
и т.д. , определяемое формулой
, определяемое формулой .
.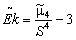 .
.


