Б-2 Основные понятия теории вероятностей.
Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий теории вероятностей является понятие случайного события (или просто события).
Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.
К понятию «вероятность» существует несколько подходов.
Современное построение теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств. Такой подход называется теоретико-множественным.
Пусть производится некоторый опыт со случайным исходом. Рассмотрим множество W всех возможных исходов опыта; каждый его элемент  будем называть элементарным событием, а множество Ω – пространством элементарных событий. Любое событие A в теоретико-множественной трактовке есть некоторое подмножество множества Ω:
будем называть элементарным событием, а множество Ω – пространством элементарных событий. Любое событие A в теоретико-множественной трактовке есть некоторое подмножество множества Ω: 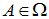 .
.
Достоверным называется событие W, которое происходит в каждом опыте.
Невозможным называется событие Æ, которое в результате опыта произойти не может.
Несовместными называются события, которые в одном опыте не могут произойти одновременно.
Суммой (объединением) двух событий A и B (обозначается A + B, A È B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
Произведением (пересечением) двух событий A и B (обозначается A × B, A Ç B) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Противоположным к событию A называется такое событие  , которое заключается в том, что событие A не происходит.
, которое заключается в том, что событие A не происходит.
События Ak (k =1, 2,..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.
Б-3 Классическое определение вероятности
По классическому определению вероятность случайного события Р (А) равна отношению числа исходов, благоприятствующих А, к общему числу исходов, составляющих пространство элементарных событий, т.е.
 . .
| |
Вычисление вероятностей при этом сводится к подсчету элементов того или иного множества и часто оказывается чисто комбинаторной задачей, иногда весьма трудной.
Классическое определение оправдано, когда существует возможность предсказания вероятности на основании симметрии условий, при которых происходит эксперимент, и вследствие этого симметрии исходов испытания, что приводит к понятию "равновозможности" исходов.
Например. Если сделанная из однородного материала геометрически правильная игральная кость подбрасывается так, что она успевает сделать достаточно большое число оборотов перед тем, как упасть, то выпадение любой из ее граней считается равновозможным исходом.
По тем же соображениям симметрии считаются равновозможными исходы такого эксперимента, как вынимание тщательно перемешанных и неотличимых на ощупь белых и черных шаров так, что после регистрации цвета каждый шар возвращается обратно в сосуд и после тщательного перемешивания производится извлечение следующего шара.
Чаще всего такая симметрия наблюдается в искусственно организованных экспериментах, какими являются азартные игры.
Таким образом, классическое определение вероятности связано с понятием равновозможности и используется для экспериментов, сводящихся к схеме случаев. Для этого необходимо, чтобы события e 1, e 2, en были несовместными, т. е. никакие два из них не могут появиться вместе; такими, что образуют полную группу, т. е. они исчерпывают собой все возможные исходы (не может быть так, что в результате опыта ни одно из них не произошло); равновозможными при условии, что эксперимент обеспечивает одинаковую возможность появления каждого из них.
Не всякий эксперимент удовлетворяет схеме случаев. Если нарушается условие симметрии, то нет схемы случаев.
Формула (1.1), "классическая формула", применялась для вычисления вероятностей событий с самого начала появления науки о случайных явлениях.
Те опыты, которые не обладали симметрией, "подгонялись" под схему случаев. В настоящее время наряду с "классической формулой" существуют способы вычисления вероятностей, когда эксперимент не сводится к схеме случаев. Для этого используется статистическое определение вероятности.
Понятие статистической вероятности будет введено позднее, а сейчас вернемся к классической формуле.
Рассмотрим следующие примеры.
Пример 1. Опыт состоит в бросании двух монет. Найти вероятность того, что появится хотя бы один герб.
Решение. Случайное событие А - появление хотя бы одного герба.
Пространство элементарных событий в данном эксперименте определяется следующими исходами: Е = {ГГ, ГР, РГ, РР}, которые соответственно обозначаются e 1, e 2, e 3, e 4. Таким образом,
E =e1, e 2, e 3, e 4; n =4.
Необходимо определить число исходов из Е, которые благоприятствуют появлению А. Это e 1, e 2, e 3; их число m =3.
Используя классическую формулу определения вероятности события А, 
Б-12 Формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например,  вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:
вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:
 – среднее число появлений события в n испытаниях.
– среднее число появлений события в n испытаниях.
Эта формула дает удовлетворительное приближение для  и
и  . При больших
. При больших  рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).
рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).
Б-13
Теорема Муавра — Лапласа — одна из предельных теорем теории вероятностей, установлена Лапласом в 1812 году. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0<р<1) и m — число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.
Рассмотрим задачу: монету подбрасывают 200 раз. Необходимо вычислить вероятность появления герба в 90 испытаниях. Применим формулу Бернулли:

Видим, что вычислить по данной формуле требуемую вероятность довольно сложно из-за громоздких вычислений. Рассмотрим методы вычислений, дающие возможность с довольно высокой точностью найти вероятность в подобных случаях. Первый из них описан в теореме Муавра- Лапласа. Эта теорема дает приближенную формулу для вычисления вероятности появления события А в схеме повторных испытаний, когда нужно вычислить появление события А ровно т раз из п испытаний.
 Теорема Муавра- Лапласа: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рп(т)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции
Теорема Муавра- Лапласа: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рп(т)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции

где
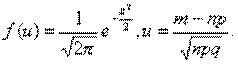
Б-14 Интегральная теорема Муавра- Лапласа: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рп(т1, т2) того, что событие А появится в п испытаниях от т1 до т2 раз. Приближенно равна определенному интегралу
 где
где

Данный интеграл называется функцией Лапласа и обозначается Ф(х).
Б-15 Следствия из интегральной теоремы Муавра—Лапласа (с выводом). Примеры.
Пусть выполнили условие применимости интегральной теоремы М.Лапласа, тогда: 1)Вероятность того, что число m наступлений события А в n испытаниях отличается от величины np не более, чем на эпсило (E) (по абсолютной величине) вычисл. по след. формуле:

2)Вер-ть того что частость (доля) m/n наступлений событий А в n испытаниях отличается от вер-ти р не более чем на D (по абсолютной величине) вычисл. По след. формуле

Б-16 Производящая функция последовательности f 0, f 1..., fn... функция

(в предположении, что этот степенной ряд сходится хотя бы для одного значения t ≠ 0). П. ф. называют также генератрисой. Последовательность f 0, f 1..., fn... может быть как числовая, так и функциональная; в последнем случае П. ф. зависит не только от t, но и от аргументов функций fn. Например, если fn = aqn где а и q — постоянные, то П. ф.

если fn — Фибоначчи числа; f 0 = 0, f 1 = 1, f n+2= f n+1+ f n, то П. ф.

если f n = Т n(х) — Чебышева многочлены: T 0(х)= 1, T n (х)= cos (n arc cos x), то П. ф.

и т.д. Знание П. ф. последовательности часто облегчает изучение свойств последней. П. ф. применяются в теории вероятностей, в теории функций и в алгебре (в теории инвариантов). Впервые метод П. ф. был применен П. Лапласом для решения некоторых проблем теории вероятностей.
Свойства
§ Моменты:

§ Дисперсия:

§ Коэффициент асимметрии:
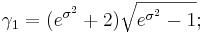
§ Коэффициент эксцесса:

Значение
Если η имеет нормальное (0, 1) распределение, то ξ = expση + m имеет логнормальное распределение с параметрами (m,σ2).
Широко используется в статистической физике, статистической геологии, экономической статистике, биологии и т.д.
Логнормальное распределение можно получить как частный случай так называемого распределения Кептейна, имеющего плотность вероятности

где G (x) - монотонная дифференцируемая функция. Если ξ имеет распределение Кептейна (m,σ2, G (x)), то η = G (ξ) имеет нормальное (0, 1) распределение. Распределение Кептейна появляется как результат применения центральной предельной теоремы к схеме суммирования вида xi + 1 = xi + zi + 1 g (xi), где zi - независимые случайные величины,  .
.
Б-38 Фишера F-распределение (F-распределение, Фишера-Снедекора распределение, Снедекора распределение) — непрерывное сосредоточенное на 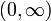 распределение вероятностей с плотностью
распределение вероятностей с плотностью

где  и
и  — параметры, а
— параметры, а  — бета-функция.
— бета-функция.
Свойства  Править
Править
При  — унимодальное (одновершинное) с положительной асимметрией распределение с модой в точке
— унимодальное (одновершинное) с положительной асимметрией распределение с модой в точке

Математическое ожидание и дисперсия равны соответственно
 при
при 
 при
при 
Cводится к бета-распределению 2-го рода (распределению типа VI по классификации Пирсона); также можно рассматривать как распределение случайной величины, представимой в форме отношения  , где независимые случайные величины
, где независимые случайные величины  и
и  имеют гамма-распределения с параметрами
имеют гамма-распределения с параметрами 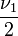 и
и  соответственно.
соответственно.
Функция распределения для  выражается через функцию распределения
выражается через функцию распределения  бета-распределения:
бета-распределения:
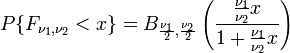 .
.
Это соотношение используется для вычисления значений F-распределения с помощью таблиц бета-распределения.
Если  и
и  целые, то F-распределением Фишера с
целые, то F-распределением Фишера с  и
и 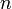 степенями свободы называется распределение F-отношения
степенями свободы называется распределение F-отношения  , где
, где  и
и  — независимые случайные величины, имеющие хи-квадрат-распределения с
— независимые случайные величины, имеющие хи-квадрат-распределения с  и
и 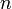 степенями свободы соответственно.
степенями свободы соответственно.
Б-44 Определение случайного процесса и его характеристики
Определение: Случайным процессом X(t) называется процесс, значение которого при любом значении аргумента tявляется случайной величиной.
Другими словами, случайный процесс представляет собой функцию, которая в результате испытания может принять тот или иной конкретный вид, неизвестный заранее. При фиксированном t=t0 X(t0) представляет собой обычную случайную величину, т.е. сечение случайного процесса в момент t0.
Примеры случайных процессов:
1. численность населения региона с течением времени;
2. число заявок, поступающих в ремонтную службу фирмы, с течением времени.
Случайный процесс можно записать в виде функции двух переменных X(t,ω), где ω?Ω, t?T, X(t, ω)? ≡ и ω – элементарное событие, Ω - пространство элементарных событий, Т – множество значений аргумента t, ≡ - множество возможных значений случайного процесса X(t, ω).
Реализацией случайного процесса X(t, ω) называется неслучайная функция x(t), в которую превращается случайный процесс X(t) в результате испытания (при фиксированном ω), т.е. конкретный вид, принимаемый случайным процессом X(t), его траектория.
Таким образом, случайный процесс X(t, ω) совмещает в себе черты случайной величины и функции. Если зафиксировать значение аргумента t, случайный процесс превращается в обычную случайную величину, если зафиксировать ω, то в результате каждого испытания он превращается в обычную неслучайную функцию. В дальнейшем изложении опустим аргумент ω, но он будет подразумеваться по умолчанию.
На рисунке 1 изображено несколько реализаций некоторого случайного процесса. Пусть сечение этого процесса при данном t является непрерывной случайной величиной. Тогда случайный процесс X(t) при данном t определяется полностью вероятности φ(x‚ t). Очевидно, что плотность φ(x, t) не является исчерпывающим описанием случайного процесса X(t), ибо она не выражает зависимости между его сечениями в разные моменты времени.
Случайный процесс X(t) представляет собой совокупность всех сечений при всевозможных значений t, поэтому для его описания необходимо рассматривать многомерную случайную величину (X(t1), X(t2), …, X(tn)), состоящей из всех сочетаний этого процесса. В принципе таких сочетаний бесконечно много, но для описания случайного процесса удаётся часть обойтись относительно небольшим количеством сочетаний.
Говорят, что случайный процесс имеет порядок n, если он полностью определяется плотностью совместного распределения φ(x1, x2, …, xn; t1, t2, …, tn) n произвольных сечений процесса, т.е. плотностью n-мерной случайной величины (X(t1), X(t2), …, X(tn)), где X(ti) – сочетание случайного процесса X(t) в момент времени ti, i=1, 2, …, n.
Как и случайная величина, случайный процесс может быть описан числовыми характеристиками. Если для случайной величины эти характеристики являются постоянными числами, то для случайного процесса – неслучайными функциями.
Математическим ожиданием случайного процесса X(t) называется неслучайная функция ax(t), которая при любом значении переменной t равна математическому ожиданию соответствующего сечения случайного процесса X(t), т.е. ax(t)=М [X(t)].
Дисперсией случайного процесса X(t) называется неслучайная функция Dx(t), при любом значении переменной t равная дисперсии соответствующего сочетания случайного процесса X(t), т.е. Dx(t)= D[X(t)].
Средним квадратическим отклонением σx(t) случайного процесса X(t) называется арифметическое значение корня квадратного из его дисперсии, т.е. σx(t)= Dx(t).
Математическое ожидание случайного процесса характеризует среднюю траекторию всех возможных его реализаций, а его дисперсия или среднее квадратическое отклонение - разброс реализаций относительно средней траектории.
Введённых выше характеристик случайного процесса оказывается недостаточно, так как они определяются только одномерным законом распределения. Если для случайного процесса Х1(t) характерно медленное изменение значений реализаций с изменением t, то для случайного процесса Х2(t) это изменение проходит значительно быстрее. Другими словами, для случайного процесса Х1(t) характерна тесная вероятностная зависимость между двумя его сочетаниями Х1(t1) и Х1(t2), в то время как для случайного процесса Х2(t) эта зависимость между сочетаниями Х2(t1) и Х2(t2) практически отсутствует. Указанная зависимость между сочетаниями характеризуется корреляционной функцией.
Б-45 МАТЕМАТИЧЕСКАЯ СТАТИСТИКА [mathematical statistics] — раздел математики, посвященный методам и правилам обработки и анализа статистических данных
Таблица 1.1
Построение интервального вариационного ряда
1. Разбивают множество значений вариант на полуинтервалы 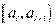 т.е. производят их группировку.
т.е. производят их группировку.
Рекомендуется количество интервалов k выбирать по формуле Стерджерса
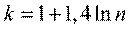 (1.4)
(1.4)
Длина интервала равна
Δ = xmax – xmin/ k
Замечание 1.
В литературе предлагается и такая форма записи формулы Стерджерса
1.Рекомендуемое число интервалов
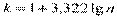
2.Величина интервала:
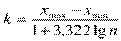
3.Строим интервал: за начало 1-го интервала берут:
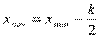
2. Считают число вариант, попавших в полуинтервал 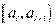 .
.
Получают значения частот 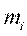 ,
, 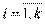 .
.
3. Интервальный ряд можно представить таблицей (табл. 1.2):
Таблица 1.2
Замечание 2.
Если варианта находится на границе интервала, то ее присоединяют к правому интервалу.
Графические изображения вариационных рядов
Для наглядности представления используют графические изображения вариационных рядов в виде:
- полигона;
- гистограммы;
- кумулянты.
Полигон, как правило, служит для изображения дискретного вариационного ряда.
Представляет собой ломаную, соединяющую точки плоскости с координатами 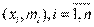 .
.
Для интервального ряда также строится полигон, только его ломаная проходит через точки 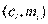 , где
, где 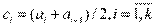 .
.
Гистограмма служит только для представления интервальных вариационных рядов и имеет вид ступенчатой фигуры из прямоугольников с основаниями, равными длине интервалов Δ, и высотами, равными частотам 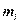 интервалов.
интервалов.
Кумулянта представляет собой ломаную, соединяющую точки с координатами 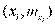 (где
(где 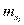 — накопленные частоты) для дискретного ряда, или точки с координатами
— накопленные частоты) для дискретного ряда, или точки с координатами 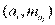 для интервального ряда.
для интервального ряда.
Эмпирической функцией распределения 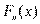 называется функция, значение которой в точке х равно накопленной частоте, т.е.
называется функция, значение которой в точке х равно накопленной частоте, т.е.
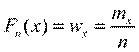 (1.6)
(1.6)
Для интервального ряда указываются не конкретные значения вариант, а только их частоты на интервалах. В этом случае эмпирическая функция распределения определена только на концах интервалов. Ее можно изобразить ломаной, проходящей через точки 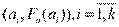 .
.
Эмпирической плотностью распределения непрерывного вариационного ряда называется функция
, 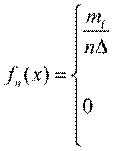 если
если 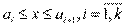
, если 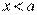 или
или 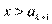
Функция 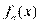 является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.
является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.
Б-48 Средняя арифметическая величина
Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным.
Иначе можно сказать, что средняя арифметическая величина - среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности.
Средняя арифметическая – наиболее распространенный на практике вид средних. Различают 2 вида арифметических средних:
Невзвешенную (простую);
Взвешенную.
Средняя арифметическая невзвешенная рассчитывается для несгруппированных данных по формуле:
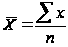 .
.
Для массовых статистических совокупностей рассчитывается взвешенная средняя арифметическая по формуле:
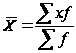 .
.
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств признака и совокупности. Например, по табл.2.1.1 можно минимальный возраст рабочих считать 17 лет. Тогда первый интервал будет от 17 до 20 лет, а максимальный возраст — 65 лет, тогда последний интервал — 50-65 лет.
Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет:
Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т. е. 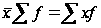 .
.
Это свойство определено требованиями правильного исчисления средней, согласно которым конкретные значения варьирующего признака уравниваются без изменения общего объема его и заменяются одним средним числом, которое как постоянный множитель выносится из-под знака суммы. Благодаря этому свойству средняя может быть использована для разного рода плановых и статистических расчетов как представитель или заменитель всех значений варьирующего признака. Так, если средний расход горючего на 1 гектар пахоты составляет 20 литров, а всего надо вспахать 2 млн. га, то всего потребуется 40 млн. литров горючего. Аналогично, если достаточно репрезентативное выборочное обследование показало, что среднегодовой надой молока на одну корову составляет 2500 литров, а всего в районе 15 тыс. коров, то общий надой составит 37,5 млн. литров.
Сумма отклонений вариантов как от простой, так и от взвешенной средней арифметической равна нулю:
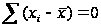 и
и 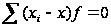
Рассмотренное свойство может быть использовано для проверки правильности исчисления средней. Если при исчислении средней арифметической 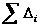 и
и 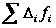 не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.
не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.
Сумма квадратов отклонений вариантов как от простой, так и от взвешенной средней меньше суммы квадратов отклонений от любой другой произвольной величины а, т. е.
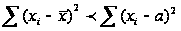 .
.
Б-2 Основные понятия теории вероятностей.
Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий теории вероятностей является понятие случайного события (или просто события).
Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.
К понятию «вероятность» существует несколько подходов.
Современное построение теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств. Такой подход называется теоретико-множественным.
Пусть производится некоторый опыт со случайным исходом. Рассмотрим множество W всех возможных исходов опыта; каждый его элемент  будем называть элементарным событием, а множество Ω – пространством элементарных событий. Любое событие A в теоретико-множественной трактовке есть некоторое подмножество множества Ω:
будем называть элементарным событием, а множество Ω – пространством элементарных событий. Любое событие A в теоретико-множественной трактовке есть некоторое подмножество множества Ω: 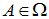 .
.
Достоверным называется событие W, которое происходит в каждом опыте.
Невозможным называется событие Æ, которое в результате опыта произойти не может.
Несовместными называются события, которые в одном опыте не могут произойти одновременно.
Суммой (объединением) двух событий A и B (обозначается A + B, A È B) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.
Произведением (пересечением) двух событий A и B (обозначается A × B, A Ç B) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.
Противоположным к событию A называется такое событие  , которое заключается в том, что событие A не происходит.
, которое заключается в том, что событие A не происходит.
События Ak (k =1, 2,..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.
Б-3 Классическое определение вероятности
По классическому определению вероятность случайного события Р (А) равна отношению числа исходов, благоприятствующих А, к общему числу исходов, составляющих пространство элементарных событий, т.е.
 . .
| |
Вычисление вероятностей при этом сводится к подсчету элементов того или иного множества и часто оказывается чисто комбинаторной задачей, иногда весьма трудной.
Классическое определение оправдано, когда существует возможность предсказания вероятности на основании симметрии условий, при которых происходит эксперимент, и вследствие этого симметрии исходов испытания, что приводит к понятию "равновозможности" исходов.
Например. Если сделанная из однородного материала геометрически правильная игральная кость подбрасывается так, что она успевает сделать достаточно большое число оборотов перед тем, как упасть, то выпадение любой из ее граней считается равновозможным исходом.
По тем же соображениям симметрии считаются равновозможными исходы такого эксперимента, как вынимание тщательно перемешанных и неотличимых на ощупь белых и черных шаров так, что после регистрации цвета каждый шар возвращается обратно в сосуд и после тщательного перемешивания производится извлечение следующего шара.
Чаще всего такая симметрия наблюдается в искусственно организованных экспериментах, какими являются азартные игры.
Таким образом, классическое определение вероятности связано с понятием равновозможности и используется для экспериментов, сводящихся к схеме случаев. Для этого необходимо, чтобы события e 1, e 2, en были несовместными, т. е. никакие два из них не могут появиться вместе; такими, что образуют полную группу, т. е. они исчерпывают собой все возможные исходы (не может быть так, что в результате опыта ни одно из них не произошло); равновозможными при условии, что эксперимент обеспечивает одинаковую возможность появления каждого из них.
Не всякий эксперимент удовлетворяет схеме случаев. Если нарушается условие симметрии, то нет схемы случаев.
Формула (1.1), "классическая формула", применялась для вычисления вероятностей событий с самого начала появления науки о случайных явлениях.
Те опыты, которые не обладали симметрией, "подгонялись" под схему случаев. В настоящее время наряду с "классической формулой" существуют способы вычисления вероятностей, когда эксперимент не сводится к схеме случаев. Для этого используется статистическое определение вероятности.
Понятие статистической вероятности будет введено позднее, а сейчас вернемся к классической формуле.
Рассмотрим следующие примеры.
Пример 1. Опыт состоит в бросании двух монет. Найти вероятность того, что появится хотя бы один герб.
Решение. Случайное событие А - появление хотя бы одного герба.
Пространство элементарных событий в данном эксперименте определяется следующими исходами: Е = {ГГ, ГР, РГ, РР}, которые соответственно обозначаются e 1, e 2, e 3, e 4. Таким образом,
E =e1, e 2, e 3, e 4; n =4.
Необходимо определить число исходов из Е, которые благоприятствуют появлению А. Это e 1, e 2, e 3; их число m =3.
Используя классическую формулу определения вероятности события А, 
Б-4Статистическое определение вероятности
Следует отметить, что классическое определение вероятности имеет существенный недостаток, заключающийся в том, что в практических задачах не всегда можно найти разумный способ выделения “равносильных случаев”. Например, затруднительно определить вероятность того, что ребенок, который должен родиться, окажется мальчиком, или определить вероятность брака в партии деталей. Из-за указанного недостатка наряду с классическим пользуются статистическим определением вероятности, опирающимся на понятие частоты (или частости).
Если классическое определение вероятности исходит из соображений равновозможности событий при некоторых испытаниях, то статистически вероятность определяется из опыта, наблюдения результатов испытания.
Назовем число m появления события А при n испытаниях частотой, а отношение mn - частостью (относительной частотой) события.
| Число подбрасываний
| Частоты появления герба
| Частость
|
|
|
| 0,5080
|
|
|
| 0,5016
|
|
|
| 0,5005
|



 будем называть элементарным событием, а множество Ω – пространством элементарных событий. Любое событие A в теоретико-множественной трактовке есть некоторое подмножество множества Ω:
будем называть элементарным событием, а множество Ω – пространством элементарных событий. Любое событие A в теоретико-множественной трактовке есть некоторое подмножество множества Ω: 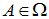 .
. , которое заключается в том, что событие A не происходит.
, которое заключается в том, что событие A не происходит. .
.

 вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:
вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона: – среднее число появлений события в n испытаниях.
– среднее число появлений события в n испытаниях. и
и  . При больших
. При больших  рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).
рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).
 Теорема Муавра- Лапласа: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рп(т)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции
Теорема Муавра- Лапласа: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Рп(т)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции
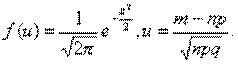
 где
где








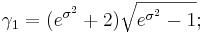


 .
. распределение вероятностей с плотностью
распределение вероятностей с плотностью
 и
и  — параметры, а
— параметры, а  — бета-функция.
— бета-функция. Править
Править — унимодальное (одновершинное) с положительной асимметрией распределение с модой в точке
— унимодальное (одновершинное) с положительной асимметрией распределение с модой в точке
 при
при 
 при
при 
 , где независимые случайные величины
, где независимые случайные величины  и
и  имеют гамма-распределения с параметрами
имеют гамма-распределения с параметрами 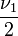 и
и  соответственно.
соответственно. выражается через функцию распределения
выражается через функцию распределения  бета-распределения:
бета-распределения: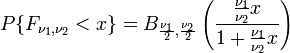 .
. и
и  целые, то F-распределением Фишера с
целые, то F-распределением Фишера с  и
и 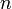 степенями свободы называется распределение F-отношения
степенями свободы называется распределение F-отношения  , где
, где  и
и  — независимые случайные величины, имеющие хи-квадрат-распределения с
— независимые случайные величины, имеющие хи-квадрат-распределения с 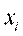
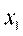
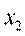
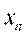
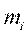
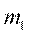
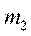
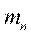
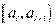 т.е. производят их группировку.
т.е. производят их группировку. 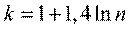 (1.4)
(1.4)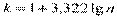
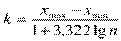
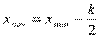
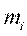 ,
, 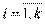 .
. 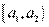
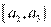
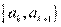
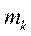
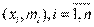 .
. 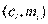 , где
, где 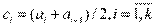 .
.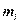 интервалов.
интервалов.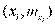 (где
(где 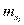 — накопленные частоты) для дискретного ряда, или точки с координатами
— накопленные частоты) для дискретного ряда, или точки с координатами 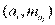 для интервального ряда.
для интервального ряда.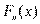 называется функция, значение которой в точке х равно накопленной частоте, т.е.
называется функция, значение которой в точке х равно накопленной частоте, т.е.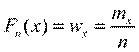 (1.6)
(1.6)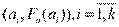 .
. 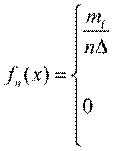 если
если 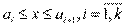
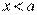 или
или 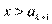
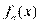 является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.
является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.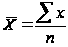 .
.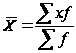 .
.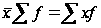 .
.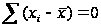 и
и 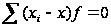
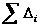 и
и 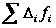 не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.
не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.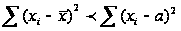 .
.


