Математическая статистика как наука начинается с работ знаменитого немецкого математика Карла Фридриха Гаусса (1777-1855), который на основе теории вероятностей исследовал и обосновал метод наименьших квадратов, созданный им в 1795 г. и примененный для обработки астрономических данных (с целью уточнения орбиты малой планеты Церера). Его именем часто называют одно из наиболее популярных распределений вероятностей – нормальное, а в теории случайных процессов основной объект изучения – гауссовские процессы.
В конце XIX в. – начале ХХ в. крупный вклад в математическую статистику внесли английские исследователи, прежде всего К.Пирсон (1857-1936) и Р.А.Фишер (1890-1962). В частности, Пирсон разработал критерий «хи-квадрат» проверки статистических гипотез, а Фишер – дисперсионный анализ, теорию планирования эксперимента, метод максимального правдоподобия оценки параметров.
В 30-е годы ХХ века поляк Ежи Нейман (1894-1977) и англичанин Э.Пирсон развили общую теорию проверки статистических гипотез, а советские математики академик А.Н. Колмогоров (1903-1987) и член-корреспондент АН СССР Н.В.Смирнов (1900-1966) заложили основы непараметрической статистики.
В сороковые годы ХХ в. румынский математик А. Вальд (1902-1950) построил теорию последовательного статистического анализа.
Б-47 Понятие вариационного ряда и его графические изображения
Пусть некоторый признак генеральной совокупности описывается случайной величиной X.
Рассмотрим выборку {х1,х2,...,хп} объема п из генеральной совокупности. этой выборки представляют собой значения случайной величины X.
На первом этапе статистической обработки производят ранжирование выборки, т.е. упорядочивание чисел х1,х2,...,хп по возрастанию.
Различные элементы выборки называются вариантами.
Частотой варианты 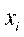 называется число
называется число 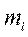 , показывающее, сколько раз эта варианта встречается в выборке.
, показывающее, сколько раз эта варианта встречается в выборке.
Частостью, относительной частотой или долей варианты называется число
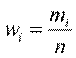 (1.1)
(1.1)
Частоты и частости называются весами.
Пусть х некоторое число. Тогда количество вариант 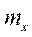 , значения которых меньше х, называется накопленной частотой, т.е.
, значения которых меньше х, называется накопленной частотой, т.е.
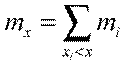 (1.2)
(1.2)
Отношение накопленной частоты к общему числу наблюдений п называется накопленной частостью:
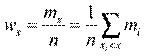
Ряд вариант, расположенных в порядке возрастания их значений, с соответствующими им весами называется вариационным рядом.
Вариационные ряды бывают:
- дискретные;
- интервальные.
Вариационный ряд называется дискретным, если он представляет собой выборку значений дискретной случайной величины.
Ряд называется непрерывным (интервальным), если он представляет выборку непрерывной случайной величины.
Общий вид дискретного вариационного ряда показан
в табл. 1.1.
Таблица 1.1
Построение интервального вариационного ряда
1. Разбивают множество значений вариант на полуинтервалы 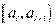 т.е. производят их группировку.
т.е. производят их группировку.
Рекомендуется количество интервалов k выбирать по формуле Стерджерса
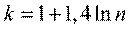 (1.4)
(1.4)
Длина интервала равна
Δ = xmax – xmin/ k
Замечание 1.
В литературе предлагается и такая форма записи формулы Стерджерса
1.Рекомендуемое число интервалов
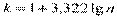
2.Величина интервала:
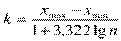
3.Строим интервал: за начало 1-го интервала берут:
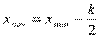
2. Считают число вариант, попавших в полуинтервал 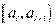 .
.
Получают значения частот 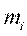 ,
, 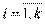 .
.
3. Интервальный ряд можно представить таблицей (табл. 1.2):
Таблица 1.2
Замечание 2.
Если варианта находится на границе интервала, то ее присоединяют к правому интервалу.
Графические изображения вариационных рядов
Для наглядности представления используют графические изображения вариационных рядов в виде:
- полигона;
- гистограммы;
- кумулянты.
Полигон, как правило, служит для изображения дискретного вариационного ряда.
Представляет собой ломаную, соединяющую точки плоскости с координатами 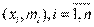 .
.
Для интервального ряда также строится полигон, только его ломаная проходит через точки 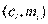 , где
, где 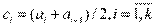 .
.
Гистограмма служит только для представления интервальных вариационных рядов и имеет вид ступенчатой фигуры из прямоугольников с основаниями, равными длине интервалов Δ, и высотами, равными частотам 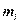 интервалов.
интервалов.
Кумулянта представляет собой ломаную, соединяющую точки с координатами 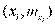 (где
(где 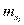 — накопленные частоты) для дискретного ряда, или точки с координатами
— накопленные частоты) для дискретного ряда, или точки с координатами 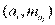 для интервального ряда.
для интервального ряда.
Эмпирической функцией распределения 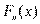 называется функция, значение которой в точке х равно накопленной частоте, т.е.
называется функция, значение которой в точке х равно накопленной частоте, т.е.
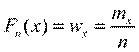 (1.6)
(1.6)
Для интервального ряда указываются не конкретные значения вариант, а только их частоты на интервалах. В этом случае эмпирическая функция распределения определена только на концах интервалов. Ее можно изобразить ломаной, проходящей через точки 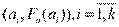 .
.
Эмпирической плотностью распределения непрерывного вариационного ряда называется функция
, 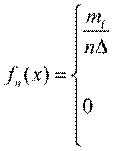 если
если 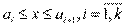
, если 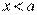 или
или 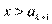
Функция 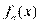 является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.
является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.
Б-48 Средняя арифметическая величина
Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным.
Иначе можно сказать, что средняя арифметическая величина - среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности.
Средняя арифметическая – наиболее распространенный на практике вид средних. Различают 2 вида арифметических средних:
Невзвешенную (простую);
Взвешенную.
Средняя арифметическая невзвешенная рассчитывается для несгруппированных данных по формуле:
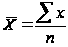 .
.
Для массовых статистических совокупностей рассчитывается взвешенная средняя арифметическая по формуле:
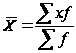 .
.
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, т.е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств признака и совокупности. Например, по табл.2.1.1 можно минимальный возраст рабочих считать 17 лет. Тогда первый интервал будет от 17 до 20 лет, а максимальный возраст — 65 лет, тогда последний интервал — 50-65 лет.
Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет:
Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т. е. 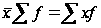 .
.
Это свойство определено требованиями правильного исчисления средней, согласно которым конкретные значения варьирующего признака уравниваются без изменения общего объема его и заменяются одним средним числом, которое как постоянный множитель выносится из-под знака суммы. Благодаря этому свойству средняя может быть использована для разного рода плановых и статистических расчетов как представитель или заменитель всех значений варьирующего признака. Так, если средний расход горючего на 1 гектар пахоты составляет 20 литров, а всего надо вспахать 2 млн. га, то всего потребуется 40 млн. литров горючего. Аналогично, если достаточно репрезентативное выборочное обследование показало, что среднегодовой надой молока на одну корову составляет 2500 литров, а всего в районе 15 тыс. коров, то общий надой составит 37,5 млн. литров.
Сумма отклонений вариантов как от простой, так и от взвешенной средней арифметической равна нулю:
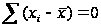 и
и 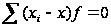
Рассмотренное свойство может быть использовано для проверки правильности исчисления средней. Если при исчислении средней арифметической 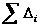 и
и 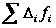 не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.
не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.
Сумма квадратов отклонений вариантов как от простой, так и от взвешенной средней меньше суммы квадратов отклонений от любой другой произвольной величины а, т. е.
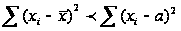 .
.



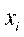 называется число
называется число 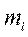 , показывающее, сколько раз эта варианта встречается в выборке.
, показывающее, сколько раз эта варианта встречается в выборке. 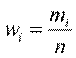 (1.1)
(1.1)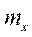 , значения которых меньше х, называется накопленной частотой, т.е.
, значения которых меньше х, называется накопленной частотой, т.е.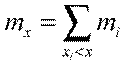 (1.2)
(1.2)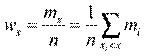
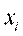
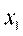
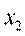
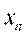
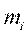
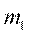
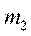
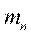
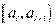 т.е. производят их группировку.
т.е. производят их группировку. 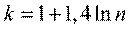 (1.4)
(1.4)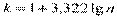
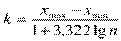
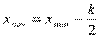
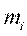 ,
, 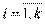 .
. 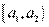
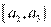
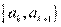
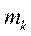
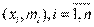 .
. 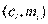 , где
, где 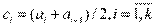 .
.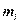 интервалов.
интервалов.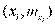 (где
(где 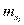 — накопленные частоты) для дискретного ряда, или точки с координатами
— накопленные частоты) для дискретного ряда, или точки с координатами 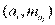 для интервального ряда.
для интервального ряда.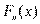 называется функция, значение которой в точке х равно накопленной частоте, т.е.
называется функция, значение которой в точке х равно накопленной частоте, т.е.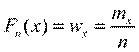 (1.6)
(1.6)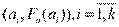 .
. 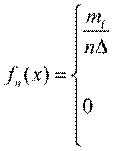 если
если 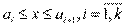
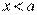 или
или 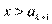
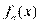 является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.
является аналогом плотности распределения случайной величины. Площадь области под графиком этой функции равна единице.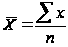 .
.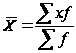 .
.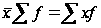 .
.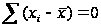 и
и 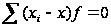
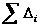 и
и 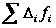 не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.
не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.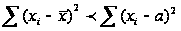 .
.

