Основные понятия
Уравнение вида
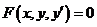 ,
,
где  - независимая переменная;
- независимая переменная;
 ,
,  - неизвестная функция и её производная,
- неизвестная функция и её производная,
называется дифференциальным уравнением первого порядка.
В случае, когда из уравнения можно выразить  , оно имеет вид
, оно имеет вид
 .
.
Уравнение называется уравнением первого порядка, разрешённым относительно производной.
Например:
 ,
,  ,
,  .
.
Решением дифференциального уравнения первого порядка называется функция  , которая при подстановке в уравнение обращает его в тождество. Решение, заданное в неявном виде
, которая при подстановке в уравнение обращает его в тождество. Решение, заданное в неявном виде  , называется интегралом дифференциального уравнения.
, называется интегралом дифференциального уравнения.
Например, функция 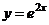 является решением дифференциального уравнения
является решением дифференциального уравнения  , так как
, так как  .
.
Теорема Коши (о существовании и единственности решения)
Если функция 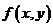 и её частная производная
и её частная производная  непрерывны в некоторой области
непрерывны в некоторой области  плоскости
плоскости  , то в некоторой окрестности любой внутренней точки
, то в некоторой окрестности любой внутренней точки  этой области существует единственное решение уравнения, удовлетворяющее условию
этой области существует единственное решение уравнения, удовлетворяющее условию  при
при  .
.
График решения дифференциального уравнения называется интегральной кривой. Теорема Коши гарантирует, что при соблюдении определённых условий через каждую внутреннюю точку области  проходит только одна интегральная кривая.
проходит только одна интегральная кривая.
Условия, которые задают значение функции  в точке
в точке  , называют начальными условиями и записывают
, называют начальными условиями и записывают
 или
или 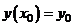 .
.
Задача нахождения решения, удовлетворяющего условию, называется задачей Коши.
Общим решением уравнения называется функция  , удовлетворяющая этому уравнению при произвольном значении
, удовлетворяющая этому уравнению при произвольном значении  .
.
Частным решением называется функция  , полученная при определённом значении
, полученная при определённом значении  .
.
Уравнение  , неявно задающее общее решение, называется общим интегралом дифференциального уравнения.
, неявно задающее общее решение, называется общим интегралом дифференциального уравнения.
Уравнение  , где
, где  - некоторое конкретное значение постоянной
- некоторое конкретное значение постоянной  , называется частным интегралом.
, называется частным интегралом.
Уравнения с разделяющимися переменными
Дифференциальное уравнение вида
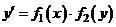 ,
,
где  и
и  - непрерывные функции, называется уравнением с разделяющимися переменными.
- непрерывные функции, называется уравнением с разделяющимися переменными.
Запишем производную  в эквивалентной форме как отношение дифференциалов
в эквивалентной форме как отношение дифференциалов  , тогда
, тогда
 .
.
Для отыскания решения этого уравнения необходимо разделить в нём переменные. Умножим обе части уравнения на  и поделим на
и поделим на  , полагая, что
, полагая, что  , имеем
, имеем
 .
.
Теперь левая часть уравнения содержит только переменную  , а правая – только
, а правая – только  . Интегрируя обе части этого уравнения, получим
. Интегрируя обе части этого уравнения, получим
 .
.
Таким образом, найден общий интеграл уравнения.
Пример 26. Найти частное решение дифференциального уравнения  при начальных условиях
при начальных условиях  .
.
Решение
Перепишем данное уравнение в виде
 .
.
Функция  является решением уравнения. Остальные решения найдём, разделив переменные в уравнении и проинтегрировав его:
является решением уравнения. Остальные решения найдём, разделив переменные в уравнении и проинтегрировав его:

Так как ранее найденное решение  можно получить из последнего соотношения, положив
можно получить из последнего соотношения, положив  , то
, то
 - общее решение.
- общее решение.
Из условия  находим
находим
 .
.
Частное решение имеет вид
 .
.



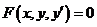 ,
, - независимая переменная;
- независимая переменная; ,
,  - неизвестная функция и её производная,
- неизвестная функция и её производная, .
. ,
,  ,
,  .
. , которая при подстановке в уравнение обращает его в тождество. Решение, заданное в неявном виде
, которая при подстановке в уравнение обращает его в тождество. Решение, заданное в неявном виде  , называется интегралом дифференциального уравнения.
, называется интегралом дифференциального уравнения.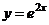 является решением дифференциального уравнения
является решением дифференциального уравнения  , так как
, так как  .
.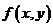 и её частная производная
и её частная производная  непрерывны в некоторой области
непрерывны в некоторой области  плоскости
плоскости  , то в некоторой окрестности любой внутренней точки
, то в некоторой окрестности любой внутренней точки  этой области существует единственное решение уравнения, удовлетворяющее условию
этой области существует единственное решение уравнения, удовлетворяющее условию  при
при  .
. в точке
в точке  , называют начальными условиями и записывают
, называют начальными условиями и записывают или
или 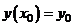 .
. , удовлетворяющая этому уравнению при произвольном значении
, удовлетворяющая этому уравнению при произвольном значении  .
. , полученная при определённом значении
, полученная при определённом значении  .
. , неявно задающее общее решение, называется общим интегралом дифференциального уравнения.
, неявно задающее общее решение, называется общим интегралом дифференциального уравнения. , где
, где  - некоторое конкретное значение постоянной
- некоторое конкретное значение постоянной 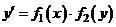 ,
, и
и  - непрерывные функции, называется уравнением с разделяющимися переменными.
- непрерывные функции, называется уравнением с разделяющимися переменными. , тогда
, тогда .
. и поделим на
и поделим на  , имеем
, имеем .
. .
. при начальных условиях
при начальных условиях  .
. .
. является решением уравнения. Остальные решения найдём, разделив переменные в уравнении и проинтегрировав его:
является решением уравнения. Остальные решения найдём, разделив переменные в уравнении и проинтегрировав его:
 , то
, то - общее решение.
- общее решение. находим
находим .
. .
.


