Электростатика. Электрический ток

301. Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины: При этом нити разошлись на угол α. Шарики по­гружаются в керосин. Определить диэлектрическую проницаемость ε керо­сина, если угол расхождения нитей при погружении шариков в керосин оста­ется неизменным. Плотность материала шариков ρ = 1600 кг/м³.

302. По тонкому кольцу радиусом R = 20 см равномерно распределен заряд с линейной плотностью τ = 0,2 мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке, нахо­дящейся на оси кольца на расстоянии h = 2R от его центра.

303. В вершинах правильного треугольника со стороной а = 10 см нахо­дятся заряды q 1 = 10 мкКл, q 2 = 20 мкКл и q 3 = 30 мкКл. Определить силу F, действующую на заряд q 1 со стороны двух других зарядов.

304. Электрическое поле создано двумя точечными зарядами q 1 = 10 нКл и q 2 =

= – 20 нКл, находящимися на расстоянии d = 20 см друг от друга. Опре­делить напряженность Е поля в точке, удаленной от первого заряда на рас­стояние r 1 = 30 см и от второго заряда на расстояние r 2 = 50 см.

305. Тонкий длинный стержень равномерно заряжен с линейной плотно­стью τ =

= 10 мкКл/м. Какова сила F, действующая на точечный заряд q = 10 нКл, находящийся вблизи средней части стержня на расстоянии а = 20 см, малом по сравнению с его длиной?

306. По тонкому полукольцу равномерно распределен заряд q = 20 мкКл с линейной плотностью τ = 0,1 мкКл/м. Определить напряженность Е элек­трического поля, создаваемого распределенным зарядом в точке, совпадаю­щей с центром кольца.

307. В вершинах квадрата находятся одинаковые заряды q = 0,3 нКл ка­ждый. Какой отрицательный заряд qо нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравно­вешена силой притяжения отрицательного заряда?

308. Поверхностная плотность σ заряда бесконечно протяженной верти­кальной плоскости равна 400 мкКл/м². К плоскости на нити подвешен заря­женный шарик массой т = 10 г. Определить заряд q шарика, если нить обра­зует с плоскостью угол

α = 30°.

309. Расстояние l между свободными зарядами q 1 = 180 нКл и q 2 = 720 нКл равно 60 см. Определить точку на прямой, проходящей через заря­ды, в которой нужно поместить третий заряд q 3 так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда. Устойчивое или неустойчивое будет равновесие?

310. На отрезке тонкого прямого проводника длиной l = 10 см равно­мерно распределен заряд с линейной плотностью τ = 3 мкКл/м. Вычислить напряженность Е электрического поля, создаваемую этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца про­водника на расстояние а, равное длине l этого отрезка.

311. На двух концентрических сферах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ1 = 120 нКл/м² и σ2 = 30 нКл/м² (рис. 1). Используя теорему Остроградского – Гаусса, найти зави­симость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, удаленной от центра на расстояние r = 1,5R, и указать направление вектора Е. Построить график зависимости Е(r).

312. Две длинные тонкостенные коаксиальные трубки радиусами R 1 = 2 см и R 2 =

= 4 см несут заряды, равномерно распределенные с линейными плотностями τ1 =

= 1 нКл/м и τ2 = – 0,5 нКл/м. Пространство между трубками заполнено эбонитом. Определить напряженность Е поля в точках, находя­щихся на расстояниях r 1 = 1 см, r 2 =

= 3 см, r 3 = 5 см от оси трубок. Построить график зависимости Е(r).

313. На двух бесконечных параллельных плоскостях равномерно распре­делены заряды с поверхностными плотностями σ1 = 160 нКл/м² и σ2 = 80 нКл/м² (рис. 2). Используя теорему Остроградского – Гаусса, найти зави­симость Е(x) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, расположенной слева от плоскостей

(в области I), и указать направле­ние вектора Е. Построить график зависимости Е(х).

Рис. 1 Рис.2

314. На металлической сфере радиусом R = 10 см находится заряд q = 1 нКл. Определить напряженность Е электрического поля в следующих точках: 1) на расстоянии r 1 = 8 см от центра сферы; 2) на ее поверхности; 3) на расстоянии r 2 = 15 см от центра сферы. Построить график зависимости Е(r).

315. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ1 = 120 нКл/м² и

σ2 = – 60 нКл/м² (рис. 3). Используя теорему Остроградского – Гаусса, найти зависимость Е(r) напряженности электрического поля от ко­ординаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, удаленной от оси цилиндров на расстояние r = 1,5 R, и указать направление вектора Е. Построить график зависимости Е(r).

Рис.3

316. На двух концентрических сферах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ1 = – 120 нКл/м² и σ2= 30 нКл/м² (рис. 1). Используя теорему Остроградского – Гаусса, найти за­висимость Е(r) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, удаленной от центра на расстояние r = 1,5 R, и указать направление вектора Е. Построить график зависимости Е(r).

317. Длинный парафиновый цилиндр радиусом R = 2 см несет заряд, равномерно распределенный с объемной плотностью ρ = 10 нКл/м³. Опреде­лить напряженность Е электрического поля в точках, находящихся от оси цилиндра на расстоянии: 1) r 1=

= 1см; 2) r 2 = 2 см; 3) r 3 = 3 см. Все точки равно­удалены от концов цилиндра. Построить график зависимости Е(r).

318. На двух бесконечных параллельных плоскостях равномерно распре­делены заряды с поверхностными плотностями σ1 = – 160 нКл/м² и σ2 = 80 нКл/м² (рис. 2). Используя теорему Остроградского – Гаусса, найти зави­симость Е(х) напряженности электрического поля от координаты для трех областей: I, II и III. Вычислить напряженность Е электрического поля в точке, расположенной между плоскостями

(в области II), и указать направле­ние вектора Е. Построить график зависимости Е(х).

319. Сплошной эбонитовый шар радиусом R == 5 см несет заряд, равно­мерно распределенный с объемной плотностью ρ = 10 нКл/м³. Определить напряженность Е электрического поля в точках: 1) на расстоянии r 1= 3 см от центра шара; 2) на поверхности шара; 3) на расстоянии r 2 = 10 см от цен­тра шара. Построить график зависимости Е(r).

320. На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями σ1 = – 120 нКл/м² и σ2 = 60 нКл/м² (рис. 3). Используя теорему Остроградского -Гаусса, найти зависимость Е(r) напряженности электрического поля от ко­ординаты для трех областей: I, II и III. Вычислить напряженность Е элек­трического поля в точке, удаленной от оси цилиндров на расстояние r = 1 ,5R, и указать направление вектора Е. Построить график зависимости Е(r).

321. Сто одинаковых капель ртути, заряженных до потенциала φо = 20 В, сливаются в одну большую каплю. Каков потенциал φ образовавшейся кап­ли?

322. Найти отношение скоростей υ 1/ υ 2 ионов Cu⁺⁺ и К.⁺, прошедших

одинаковую разность потенциалов.

323. На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью τ = 10 нКл/м. Вычислить потенциал φ, созда­ваемый этим зарядом в точке, расположенной на оси проводника и удаленной

от ближайшего конца проводника на расстояние, равное длине этого отрезка.

324. Тонкий стержень согнут в кольцо радиусом R = 10 см и равномерно заряжен с линейной плотностью τ = 300 нКл/м. Какую работу А надо со­вершить, чтобы перенести заряд q = 5 нКл из центра кольца в точку, распо­ложенную на расстоянии h =

= 20 см от его центра?

325. Какова потенциальная энергия П системы четырех одинаковых то­чечных зарядов q = 10 нКл, расположенных в вершинах квадрата со стороной длиной а =

= 10 см?

326. Определить линейную плотность τ бесконечно длинной заряженной нити, если работа А сил поля по перемещению заряда q = 1 нКл с расстоя­ния r 1 = 5 см до расстояния r 2 = 2 см в направлении, перпендикулярном ни­ти, равна 50 мкДж.

327. Электростатическое поле создается шаром радиусом R = 8 см, рав­номерно заряженным с объемной плотностью ρ = 10 нКл/м³. Определить раз­ность потенциалов ∆φ между двумя точками этого поля, лежащими на рас­стояниях r 1 = 10 см и r 2. = 15 см от центра шара.

328. Тонкий стержень, согнут в полукольцо. Стержень заряжен с линей­ной плотностью τ = 133 нКл/м. Какую работу А надо совершить, чтобы пе­ренести заряд точечный q = 6,7 нКл из центра полукольца в бесконечность?

329. Тонкие стержни образуют квадрат со стороной длиной а. Стержни заряжены с линейной плотностью τ = 1,33 нКл/м. Определить потенциал φ в центре квадрата.

330. Протон, начальная скорость υо которого равна 100 км/с, влетает в однородное электрическое поле напряженностью Е = 300 В/см так, что век­тор скорости совпадает с направлением линий напряженности. Какой путь l, должен пройти протон в направлении линий поля, чтобы его скорость υ уве­личилась в п = 2 раза?

331. В плоский воздушный конденсатор вдвинули плитку парафина тол­щиной h =

= 1 см, которая вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние d между пластинами, чтобы получить прежнюю емкость?

332. Уединенная металлическая сфера электроемкостью С = 10пф заря­жена до потенциала φ = 3 кВ. Определить энергию W поля, заключенную в сферическом слое, ограниченном сферой и концентрической с ней сфериче­ской поверхностью, радиус которой в п = 3 раза больше радиуса сферы.

333. Конденсатор электроемкостью С1 = 0,2 мкФ был заряжен до разно­сти потенциалов U 1 = 320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U 2 = 450 В, напряжение U на нем изменилось до 400 В. Вычислить емкость С2 второго конденсатора.

334. Электроемкость С плоского конденсатора равна 111 пФ. Диэлек­трик – фарфор. Конденсатор зарядили до разности потенциалов U = 600 В и отключили от источника напряжения. Какую работу А нужно совершить, чтобы вынуть диэлектрик из конденсатора? Трение диэлектрика о пластины конденсатора пренебрежимо мало.

335. Шар радиусом R 1 = 6 см заряжен до потенциала φ1 = 300 В, а шар радиусом R 2 = 4 см – до потенциала φ2 = 500 В. Определить потенциал φ шаров после того, как их соединили металлическим проводником. Емкостью соединительного проводника пренебречь.

336. Конденсатор электроемкостью C 1 = 600 пФ зарядили до разности потенциалов U = 1,5 кВ и отключили от источника тока. Затем к конденса­тору присоединили параллельно второй, незаряженный конденсатор электро­емкостью С 2 =

= 400 пФ. Определить энергию W, израсходованную на образо­вание искры, проскочившей при соединении конденсаторов.

337. Между пластинами плоского конденсатора находится плотно приле­гающая стеклянная пластинка. Конденсатор заряжен до разности потенциа­лов U 1 = 100 В. Какова будет разность потенциалов U 2, если вытащить стек­лянную пластинку из конденсатора?

338. Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r = 10 см каждая. Расстояние d 1 между пластинами равно 1 см. Конденсатор зарядили до разности потенциалов U = 1,2 кВ и отключили от источника тока. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d 2 = 3,5 см?

339. Конденсатор электроемкостью C1 = 0,6 мкФ был заряжен до разно­сти потенциалов U 1 = 300 В и соединен последовательно со вторым конден­сатором электроемкостью С2 = 0,4 мкФ, заряженным до разности потенциа­лов U 2 = 150 В. Найти заряд ∆ q, перетекший с пластин первого конденсатора на второй.

340. Сплошной парафиновый шар радиусом R = 10 см равномерно за­ряжен с объемной плотностью ρ = 10 нКл/м³. Определить энергию W элек­трического поля, сосредоточенную в самом шаре.

341. При силе тока I 1 = 3 А во внешней цепи батареи аккумуляторов вы­деляется мощность Р 1 = 18 Вт, а при силе тока I 2 = 1 А – соответственно мощность Р 2 = 10 Вт. Определить ЭДС ξ и внутреннее сопротивление r ба­тареи.

342. По проводнику сопротивлением R = 3 Ом течет ток, сила которого равномерно возрастает. Количество теплоты Q, выделившееся в проводнике за время t= 8 с, равно 200 Дж. Определить количество электричества q, про­текшее за это время по проводнику. В момент времени t 0, принятый за на­чальный, сила тока I в проводнике равна нулю.

343. К источнику тока с ЭДС ξ = 1,5В присоединили катушку с сопро­тивлением R= 0,1 Ом. Амперметр показал силу тока, равную I 1 = 0,5 А. Ко­гда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока I в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления r 1 и r 2 первого и второго источников тока.

344. Сила тока в проводнике сопротивлением R = 12 Ом равномерно убывает от

I 0 = 5 А до I = 0 А в течение времени t = 10 с. Определить коли­чество теплоты Q, которое выделяется в этом проводнике за указанный про­межуток времени.

345. К зажимам батареи аккумуляторов присоединен нагреватель. ЭДС ξ батареи равна 24 В, внутреннее сопротивление r = 1 Ом. Нагреватель, вклю­ченный в цепь, потребляет мощность Р = 80 Вт. Вычислить силу тока I в це­пи и КПД η нагревателя.

346. Сила тока в проводнике равномерно увеличивается от I 0 = 0 А до некоторого максимального значения I max в течение времени t = 10 с. За это время в проводнике выделилось количество теплоты Q = 1 кДж. Определить скорость нарастания dI/dt тока в проводнике, если сопротивление R его равно 3 Ом.

347. В сеть с напряжением U = 100 В подключили катушку с сопротивле­нием

R 1 = 2 кОм и вольтметр, соединенные последовательно. Вольтметр по­казал напряжение U 1 = 80 В. Когда катушку заменили другой, вольтметр по­казал напряжение U 2 = 60 В. Определить сопротивление R 2 другой катушки.

348.Сила тока в проводнике изменяется со временем по закону I = I 0 sin ω t. Найти заряд q, проходящий через поперечное сечение проводника за время t, равное половине периода Т, если начальная сила тока I 0 = 10 А, циклическая частота

ω = 50 π с‾¹.

349. Определить силу тока I кз короткого замыкания источника ЭДС, ес­ли при внешнем сопротивлении R 1 = 50 Ом сила тока в цепи I 1 = 0,2 А, а при сопротивлении R 2 = 110 Oм сила тока I 2 = 0,1 А.

350. При выключении источника тока сила тока в цепи убывает со време­нем по закону I = I 0 e^{α t},где I 0 = 10 А, α = 5·10² с‾¹. Определить количество теплоты Q, которое выделится в резисторе сопротивлением R = 5 Ом после выключения источника тока.

351. Две батареи аккумуляторов с ЭДС ξ1 = ξ2 = 100 В и четыре резисто­ра с сопротивлениями R 1 = 20 Ом, R 2 = 10 Ом, R 3 = 40 Ом и R 4 = 30 Ом со­единены, как показано на рис. 4. Найти показание I A амперметра. Внутрен­ними сопротивлениями r, батарей аккумуляторов пренебречь.

 

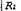
Рис. 4 Рис. 5

352. Три источника тока с ЭДС ξ1 = 11 В, ξ2 = 4 В и ξ3 = 6 В и три реостата с сопротивлениями R 1 = 5 Ом, R 2 = 10 Ом и R 3 = 2 Ом соединены, как показано на

рис. 5. Определить силы токов I, в реостатах. Внутренние со­противления r, источников тока пренебрежимо малы.

353. Два гальванических элемента с ЭДС ξ1 = ξ2, два резистора с сопро­тивлениями R 1 = R 2 = 100 Ом и вольтметр с сопротивлением Ry = 150 Ом со­единены, как показано на рис. 6. Показание вольтметра U = 150 В. Найти ЭДС ξ1 и ξ2 гальванических элементов, пренебрегая их внутренними сопро­тивлениями r.

 

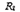
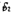
Рис.6 Рис.7

354. Две батареи аккумуляторов с ЭДС ξ1 = 130 В и ξ2 = 117 В и три ре­зистора с сопротивлениями R 1 = 1 Ом, R 2 = 0,6 Ом и R 3 =240м соединены, как показано на рис.7.Определить силы токов I, в отдельных ветвях элек­трической цепи. Внутренние сопротивления r, батарей аккумуляторов пре­небрежимо малы.

355. Три резистора с сопротивлениями r 1 = 5 Ом, R 2 = 1 Ом и R 3 = 3 Ом, а также источник тока с ЭДС ξ = 1,4 В соединены как показано на рис, 8. Определить ЭДС ξ1 источника тока, который надо подключить в цепь меж­ду точками А и В, чтобы в резисторе с сопротивлением R 3 шел ток силой I 3 = 1 А в направлении, указанном стрелкой. Внутренним сопротивлением r источника тока пренебречь.

 

Рис. 8 Рис. 9

356. Два гальванических элемента имеют ЭДС ξ1 = 2 В и ξ2 = 4 В, рези­стор R 1 имеет сопротивление 0,5 Ом (рис.9). Падение напряжения U 1 на ре­зисторе с сопротивлением R 2 равно 1 В, причем ток через этот резистор на­правлен справа налево. Найти показание I A амперметра. Внутренние сопро­тивления r, гальванических элементов пренебрежимо малы.

357. Три батареи аккумуляторов с ЭДС ξ1 = 1 В, ξ2 = 3 В и ξ3 = 5 В и три резистора с сопротивлениями R 1 = 2 Ом, R 2 = 4 Ом и R 3 = 2 Ом соедине­ны, как показано на

рис. 10. Определить силу тока I, в каждой ветви элек­трической цепи. Внутренними сопротивлениями r, батарей аккумуляторов пренебречь.

 

Рис.10 Рис.11

 

358. Источник тока имеет ЭДС ξ = 2 В, резисторы имеют сопротивления R 1 =

= 30 Ом, R 2 = 45 Ом и R 3 = 200 Ом. Найти силу тока I, в каждой ветви мостика Уитстона (рис. 11) при условии, что гальванометр показывает силу тока I г = 0 А. Внутреннее сопротивление r источника тока пренебрежимо мало.

359. Две батареи аккумуляторов имеют ЭДС ξ1 = 2 В и ξ2 = 3 В, рези­стор R 2 имеет сопротивление 1,5 кОм, сопротивление амперметра R A = 0,5 кОм (рис. 12). Падение напряжения U 1 на резисторе с сопротивлением R 1 равно 1 В, причем ток через этот резистор течет сверху вниз. Найти пока­зание I A амперметра. Внутренними сопротивлениями r, батарей аккумуля­торов пренебречь.

 

Рис.12 Рис.13

360. Два источника тока с ЭДС ξ1 = 4 В и ξ2 = 3 В и три резистора с со­противлениями R 1 = 2 Ом, R 2 =6 Ом и R 3 = 1 Ом соединены, как показано на рис. 13. Пренебрегая внутренними сопротивлениями r, источников тока, определить силу тока I 3 в резисторе с сопротивлением R 3 и падение напря­жения U 3 на концах этого резистора.

361. Определить суммарный импульс р электронов в прямом проводе длиной l = = 500 м, по которому течет ток I = 20 А.

362. Исходя из модели свободных электронов, определить среднее число < z > соударений, которые испытывает электрон за время t = 1 с, находясь в ме­талле, если концентрация п свободных электронов равна 10²⁹ м‾³. Удельную проводимость γ металла принять равной 10 МСм/м.

363. Сила тока I в цепи, состоящей из термопары с сопротивлением R = 4 Ом и гальванометра с сопротивлением R г = 80 Ом, равна 26 мкА при разности температур ∆ t спаев, равной 50°С. Определить постоянную k тер­мопары.

364. В медном проводнике длиной l = 2 м и площадью S поперечного сечения, равной 0,4 мм², течет ток. При этом за время t = 1 с выделяется ко­личество теплоты

Q = 0,35 Дж. Определить число N электронов, которое проходит за это время через поперечное сечение проводника.

365. Металлический стержень движется вдоль своей оси со скоростью υ =

= 200 м/с. Определить заряд q, который протечет через гальванометр, под­ключаемый к концам стержня, при резком его торможении, если длина l стержня равна 10 м, а сопротивление R всей цепи (включая цепь гальвано­метра) равно 10 мОм.

366. Термопара медь – константан с сопротивлением R = 5 Ом присое­динена к гальванометру, сопротивление R г которого равно 100 Ом. Один спай термопары погружен в тающий лед, другой – в горячую жидкость. Сила тока I в цепи равна

37 мкА. Постоянная термопары k = 43 мкВ/К. Опреде­лить температуру t жидкости.

367. Определить напряженность Е электрического поля в алюминиевом проводнике объемом V = 10 см³, если при прохождении по нему постоянного тока за время t = 5 мин выделилось количество теплоты Q = 2,3 кДж.

368. Металлический диск радиусом R = 0,5 м равномерно вращается с угловой скоростью ω = 10⁴ рад/с относительно неподвижной оси, перпенди­кулярной плоскости диска и проходящей через его центр. Определите раз­ность потенциалов U между центром диска и его крайними точками.

369. Термопара висмут – железо с постоянной k = 92 мкВ/К и сопротив­лением

R = 5 Ом присоединена к гальванометру сопротивлением R г=110 Ом. Какую силу тока I покажет гальванометр, если температура хо­лодного спая термопары t 1 = 0°С, а горячего спая t 2 = 100°С?

370. Плотность j электрического тока в медном проводнике равна 10 А/см². Определить удельную тепловую мощность w тока.

371. При электролизе медного купороса (CuS04) в течение времени t = 1 ч при силе тока I = 1 А на катоде выделилась медь массой т = 1,66 г. Определить коэффициент полезного действия η установки.

372. Посередине между электродами ионизационной камеры пролетела а-частица, двигаясь параллельно электродам, и образовала на своем пути це­почку ионов. Спустя какое время t после пролета α – частицы ионы дойдут до электродов, если расстояние d между электродами равно 4 см, разность по­тенциалов U = 5 кВ и подвижность ионов обоих знаков в среднем b = 2 см²/(В·с)?

373. Определить, во сколько раз увеличится плотность тока насыщения I нас при повышении температуры вольфрамового катода от температуры Т 1 = 2000 К до температуры Т 2 = 2500 К.

374. Определить число N атомов никеля, которое выделится на поверх­ности электрода площадью S = 1 см² при электролизе сульфата никеля (NiS04) за время t = 5 мин при плотности тока j = 10 А/м².

375. Определить силу тока насыщения I нас между пластинами конденса­тора, если под действием внешнего ионизатора в объеме V 0= 1 см³ про­странства между пластинами конденсатора за время t = 1 с образуется п = 10⁷ пар ионов, каждый из которых несет один элементарный заряд. Рас­стояние d между пластинами конденсатора равно 1 см, площадь S пластины равна 100 см².

376. В электронной лампе ток насыщения I нас достигает значения 2,86 мкА при температуре вольфрамового волоска катода T = 2 кК. Опреде­лить диаметр d волоска катода, если длина его l = 2 см. Эмиссионная посто­янная С для вольфрама равна

6,02·10⁵ А/(м²·К²).

377. Определить скорость и (в мкм/ч), с которой растет слой меди на плоской поверхности металлической пластинки при электролизе медного ку­пороса (CuS04), если плотность тока j, протекающего через электролит, рав­на 80 А/м².

378. Определить концентрацию п ионов между пластинами плоского воздушного конденсатора емкостью С = 6,6 пф, если воздух ионизируется внешним ионизатором и при напряжении U = 450 В сила тока I равна 7 мкА. Насыщение не имеет места.

379. Определить работу выхода А электронов из металла, если повыше­ние температуры нити накала, сделанной из этого металла, от температуры T 1 = 2380 К до температуры Т 2 = 2381 К увеличивает плотность тока насы­щения j нас в электронной лампе на п = 1 %.

380. При электролизе нитрата серебра (AgN03) было израсходовано W = 2,1 кДж электрической энергии. При этом на электроде выделилось серебро массой m = 500 мг. Определить разность потенциалов U на электродах, если коэффициент полезного действия η всей установки составляет 85 %.