ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
(Пособие для студентов заочного отделения)
Составитель В.Е.Алексеев
Начальные понятия
Определение графа
Термин «граф» неоднозначен и это легко обнаружить, сравнивая определения графа, приводимые в разных книгах по теории графов. Однако во всех этих определениях есть и общее. В любом случае граф состоит из двух множеств – множества вершин и множества ребер, причем для каждого ребра указана пара вершин, которые это ребро соединяет. Здесь будут рассматриваться только конечные графы, то есть такие, у которых оба множества конечны. Чтобы получить законченное определение графа того или иного типа, необходимо уточнить еще следующие три момента.
1.Ориентированный или неориентированный?
Прежде всего нужно договориться, считаем ли мы пары  и
и 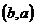 различными. Если да, то говорят, что рассматриваются упорядоченные пары (порядок элементов в паре важен), если нет – неупорядоченные. Если ребро e соединяет вершину a с вершиной b и пара
различными. Если да, то говорят, что рассматриваются упорядоченные пары (порядок элементов в паре важен), если нет – неупорядоченные. Если ребро e соединяет вершину a с вершиной b и пара 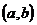 считается упорядоченной, то это ребро называется ориентированным, вершина a – его началом, вершина b – концом. Если же эта пара считается неупорядоченной, то ребро называется неориентированным, а обе вершины – его концами. Заметим, что неориентированное ребро, соединяющее a с b, соединяет и b с a, для ориентированного же это неверно. Чаще всего рассматривают графы, в которых все ребра имеют один тип – либо ориентированные, либо неориентированные. В соответствии с этим и весь граф называют ориентированным или неориентированным.
считается упорядоченной, то это ребро называется ориентированным, вершина a – его началом, вершина b – концом. Если же эта пара считается неупорядоченной, то ребро называется неориентированным, а обе вершины – его концами. Заметим, что неориентированное ребро, соединяющее a с b, соединяет и b с a, для ориентированного же это неверно. Чаще всего рассматривают графы, в которых все ребра имеют один тип – либо ориентированные, либо неориентированные. В соответствии с этим и весь граф называют ориентированным или неориентированным.
2. Кратные ребра.
Следующий пункт, требующий уточнения – могут ли два разных ребра соединять одну и ту же пару вершин? Если да, то говорят, что в графе допускаются кратные ребра. Граф с кратными ребрами называют также мультиграфом.
3. Петли.
Ребро, которому поставлена в соответствие пара вида 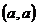 , то есть ребро, соединяющее вершину a с нею же самой, называется петлей. Если такие ребра не допускаются, то говорят, что рассматриваются графы без петель.
, то есть ребро, соединяющее вершину a с нею же самой, называется петлей. Если такие ребра не допускаются, то говорят, что рассматриваются графы без петель.
Комбинируя эти три признака, можно получить разные варианты определения понятия графа. Особенно часто встречаются неориентированные графы без петель и кратных ребер. Такие графы называют обыкновенными, или простыми. Если в графе нет кратных ребер, то есть для каждой пары вершин имеется не более одного соединяющего их ребра, то можно просто отождествить ребра с соответствующими парами вершин – считать, что ребро это и есть пара вершин. Чтобы исключить петли, достаточно оговорить, что вершины, образующие ребро, должны быть различны. Это приводит к следующему определению обыкновенного графа.
Определение. Обыкновенным графом называется пара 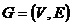 , где V – конечное множество, E – множество неупорядоченных пар различных элементов из V. Элементы множества V называются вершинами графа, элементы множества E – его ребрами.
, где V – конечное множество, E – множество неупорядоченных пар различных элементов из V. Элементы множества V называются вершинами графа, элементы множества E – его ребрами.
Определения других типов графов без кратных ребер легко получить из этого: если заменить слово «неупорядоченных» на «упорядоченных», получится определение ориентированного графа без петель, если убрать слово «различных», получится определение графа с петлями. Ориентированный граф коротко называют орграфом.
Графы и бинарные отношения
Напомним, что бинарным отношением на множестве A называется любое подмножество R множества 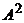 , состоящего из всевозможных упорядоченных пар элементов множества A. Сравнивая с тем, что говорилось выше об определениях различных типов графов, видим, что понятие бинарного отношения эквивалентно понятию ориентированного графа с петлями. Другие типы графов без кратных ребер – это частные виды бинарных отношений. Отношение R называется рефлексивным, если для любого
, состоящего из всевозможных упорядоченных пар элементов множества A. Сравнивая с тем, что говорилось выше об определениях различных типов графов, видим, что понятие бинарного отношения эквивалентно понятию ориентированного графа с петлями. Другие типы графов без кратных ребер – это частные виды бинарных отношений. Отношение R называется рефлексивным, если для любого 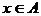 пара (x,x) принадлежит R, и антирефлексивным, если ни одна такая пара не принадлежит R. Оно называется симметричным, если для любых
пара (x,x) принадлежит R, и антирефлексивным, если ни одна такая пара не принадлежит R. Оно называется симметричным, если для любых 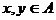 из
из 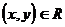 следует
следует 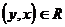 . Обыкновенный граф – не что иное, как антирефлексивное симметричное отношение.
. Обыкновенный граф – не что иное, как антирефлексивное симметричное отношение.
Откуда берутся графы
Легко найти примеры графов в самых разных областях науки и практики. Сеть дорог, трубопроводов, электрическая цепь, структурная формула химического соединения, блок-схема программы – в этих случаях графы возникают очень естественно и видны «невооруженным глазом».
Немало поводов для появления графов и в самой математике. Наиболее очевидный пример – любой многогранник в трехмерном пространстве. Вершины и ребра многогранника можно рассматривать как вершины и ребра графа. При этом надо ясно осознавать, что рассматривая многогранник как граф, мы теряем собственно геометрическую информацию о расположении его элементов в пространстве: на рисунке 2 показаны три способа изобразить один и тот же граф трехмерного куба.
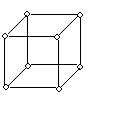
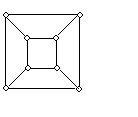
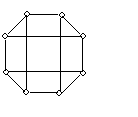
Рис. 2
Еще один способ образования графов из геометрических объектов иллюстрирует рисунок 3. Слева показаны восемь кругов на плоскости, а справа – граф, в котором каждая вершина соответствует одному из этих кругов и две вершины соединены ребром в том и только том случае, когда соответствующие круги пересекаются. Такие графы называют графами пересечений. Можно построить граф пересечений семейства интервалов на прямой, или дуг окружности, или параллелепипедов.
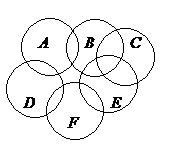
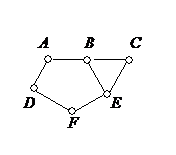
Рис.3
Число графов
Возьмем какое-нибудь множество V, состоящее из n элементов, и будем рассматривать всевозможные (обыкновенные!) графы с множеством вершин V. Обозначим число таких графов через 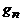 . Эти графы различаются только множествами ребер, а каждое ребро – это неупорядоченная пара различных элементов из V. В комбинаторике такие пары называются сочетаниями из n по 2, их число равно
. Эти графы различаются только множествами ребер, а каждое ребро – это неупорядоченная пара различных элементов из V. В комбинаторике такие пары называются сочетаниями из n по 2, их число равно 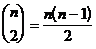 . Каждая пара может быть включена или не включена в множество ребер графа. Применяя правило произведения, приходим к следующему результату.
. Каждая пара может быть включена или не включена в множество ребер графа. Применяя правило произведения, приходим к следующему результату.
Теорема 1. 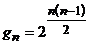 .
.
Подграф
Граф 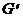 называется подграфом графа G, если
называется подграфом графа G, если 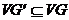 ,
, 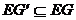 . Всякий подграф может быть получен из графа удалением некоторых вершин и ребер. На рисунке 4 изображены граф G и его подграфы
. Всякий подграф может быть получен из графа удалением некоторых вершин и ребер. На рисунке 4 изображены граф G и его подграфы  .
.
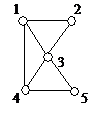
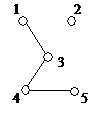
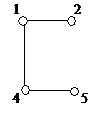
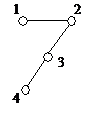
G 
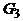
Рис. 4
Подграф 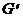 графа G называется остовным, если
графа G называется остовным, если 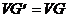 . Остовный подграф может быть получен из графа удалением некоторых ребер, вершины же остаются в неприкосновенности. На рисунке 4
. Остовный подграф может быть получен из графа удалением некоторых ребер, вершины же остаются в неприкосновенности. На рисунке 4  – остовный подграф графа G, а
– остовный подграф графа G, а 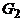 и
и 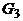 не являются остовными подграфами.
не являются остовными подграфами.
Другая важная разновидность подграфов – порожденные подграфы. Пусть задан граф 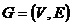 и в нем выбрано множество вершин
и в нем выбрано множество вершин 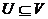 . Рассмотрим подграф
. Рассмотрим подграф 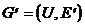 , где
, где 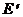 состоит из всех тех ребер графа G, у которых оба конца принадлежат U. Говорят, что этот подграф порожден множеством вершин U. Он обозначается через
состоит из всех тех ребер графа G, у которых оба конца принадлежат U. Говорят, что этот подграф порожден множеством вершин U. Он обозначается через 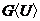 . Порожденный подграф может быть получен из графа удалением «лишних» вершин, т.е. вершин, не принадлежащих U, причем при удалении вершины удаляются и все инцидентные ей ребра.
. Порожденный подграф может быть получен из графа удалением «лишних» вершин, т.е. вершин, не принадлежащих U, причем при удалении вершины удаляются и все инцидентные ей ребра.
На рисунке 4 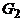 – подграф графа G, порожденный множеством вершин {1,2,4,5}, т.е.
– подграф графа G, порожденный множеством вершин {1,2,4,5}, т.е. 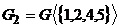 , а подграф
, а подграф 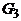 не является ни остовным, ни порожденным.
не является ни остовным, ни порожденным.
Некоторые специальные графы
Рассмотрим некоторые особенно часто встречающиеся графы.
Пустой граф – граф, не содержащий ни одного ребра. Пустой граф с множеством вершин {1,2,..., n } обозначается через 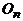 .
.
Полный граф – граф, в котором каждые две вершины смежны. Полный граф с множеством вершин {1,2,..., n } обозначается через 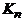 . Граф
. Граф 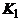 , в частности, имеет одну вершину и ни одного ребра.
, в частности, имеет одну вершину и ни одного ребра.
Цепь (путь) 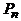 – граф с множеством вершин {1,2,..., n } и множеством ребер
– граф с множеством вершин {1,2,..., n } и множеством ребер 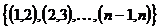 .
.
Цикл 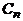 – граф, который получается из
– граф, который получается из 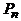 добавлением ребра
добавлением ребра 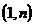 .
.
Дополнительный граф
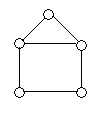
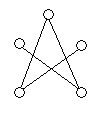
Дополнительным графом (или дополнением) к обыкновенному графу G называется граф 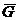 , у которого множество вершин то же, что у G, и две различные вершины смежны тогда и только тогда, когда они не смежны в G. Например,
, у которого множество вершин то же, что у G, и две различные вершины смежны тогда и только тогда, когда они не смежны в G. Например, 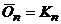 . Другой пример показан на рисунке 5. Очевидно, всегда
. Другой пример показан на рисунке 5. Очевидно, всегда 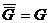 .
.
G 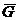
Рис. 5
Изоморфизм
На рисунке 6 изображены два графа с одним и тем же множеством вершин 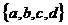 . При внимательном рассмотрении можно обнаружить, что это разные графы – в левом имеется ребро
. При внимательном рассмотрении можно обнаружить, что это разные графы – в левом имеется ребро 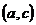 , в правом же такого нет. В то же
, в правом же такого нет. В то же
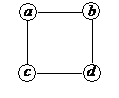
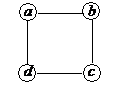

Рис. 6
время, если не обращать внимания на наименования вершин, то эти графы явно
одинаково устроены: каждый из них – цикл из четырех вершин. Во многих случаях при исследовании строения графов имена или номера вершин не играют роли и такие графы, один из которых получается из другого переименованием вершин, можно считать одинаковыми. Для того, чтобы это можно было делать «на законном основании», вводится понятие изоморфизма графов.
Определение. Графы  и
и 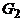 называются изоморфными, если существует такая биекция f множества
называются изоморфными, если существует такая биекция f множества 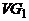 на множество
на множество 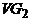 , что
, что 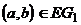 тогда и только тогда, когда
тогда и только тогда, когда 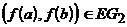 . Отображение f в этом случае называется изоморфизмом
. Отображение f в этом случае называется изоморфизмом  в
в 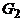 .
.
Тот факт, что графы  и
и 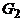 изоморфны, записывается так:
изоморфны, записывается так: 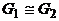 .
.
Для графов, изображенных на рисунке 6, изоморфизмом является, например, отображение, задаваемое таблицей:
x (вершина графа  ) )
| a
| b
| c
| d
|
f (x) (вершина графа 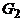 ) )
| a
| b
| d
| c
|
Заметим, что в этом примере есть и другие изоморфизмы первого графа во второй.
Это определение изоморфизма годится и для ориентированных графов, нужно только обе упоминаемые в нем пары вершин считать упорядоченными.
Изоморфизм – бинарное отношение на множестве графов. Очевидно, это отношение рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности. Классы эквивалентности называются абстрактными графами. Когда говорят, что рассматриваются абстрактные графы, это означает, что изоморфные графы считаются одинаковыми. Абстрактный граф можно представлять себе как граф, у которого стерты имена (пометки) вершин, поэтому абстрактные графы иногда называют также непомеченными графами.
В общем случае узнать, изоморфны ли два графа, достаточно сложно. Если буквально следовать определению, то нужно перебрать все биекции множества вершин одного из них в множество вершин другого и для каждой из этих биекций проверить, является ли она изоморфизмом. Для n вершин имеется n! биекций и эта работа становится практически невыполнимой уже при не очень больших n (так, 10! = 3628800, 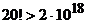 ). Однако для многих конкретных пар графов их неизоморфность устанавливается довольно легко. Рассмотрим, например, графы, изображенные на рисунке 7. Так как при изоморфизме пара смежных вершин переходит в пару смежных, а пара несмежных – в пару несмежных, то ясно, что число ребер у двух изоморфных графов должно быть одинаковым. Поэтому сразу можно сказать, что графы
). Однако для многих конкретных пар графов их неизоморфность устанавливается довольно легко. Рассмотрим, например, графы, изображенные на рисунке 7. Так как при изоморфизме пара смежных вершин переходит в пару смежных, а пара несмежных – в пару несмежных, то ясно, что число ребер у двух изоморфных графов должно быть одинаковым. Поэтому сразу можно сказать, что графы  и
и 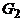 , у которых разное количество ребер, неизоморфны. У графов
, у которых разное количество ребер, неизоморфны. У графов  и
и 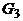 одинаковое число ребер, но они тоже неизоморфны. Это можно установить, сравнивая степени вершин. Очевидно, при изоморфизме каждая вершина переходит в вершину той же степени. Но если выписать степени всех вершин графа
одинаковое число ребер, но они тоже неизоморфны. Это можно установить, сравнивая степени вершин. Очевидно, при изоморфизме каждая вершина переходит в вершину той же степени. Но если выписать степени всех вершин графа  в неубывающем порядке, то получится последовательность (2,2,3,3,3,3), а для графа
в неубывающем порядке, то получится последовательность (2,2,3,3,3,3), а для графа 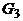 получится последовательность (2,2,2,3,3,4). Из того, что эти последовательности различны, следует неизоморфность двух графов. С графами
получится последовательность (2,2,2,3,3,4). Из того, что эти последовательности различны, следует неизоморфность двух графов. С графами  и
и 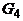 дело обстоит немного сложнее – у них и наборы степеней одинаковы. Все же и эти графы неизоморфны: можно заметить, что в
дело обстоит немного сложнее – у них и наборы степеней одинаковы. Все же и эти графы неизоморфны: можно заметить, что в 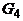 есть подграф, являющийся циклом длины 3, а в
есть подграф, являющийся циклом длины 3, а в  таких нет. Ясно, что при изоморфизме каждый подграф одного графа переходит в изоморфный ему подграф другого.
таких нет. Ясно, что при изоморфизме каждый подграф одного графа переходит в изоморфный ему подграф другого.
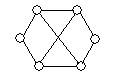
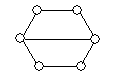
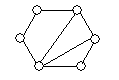
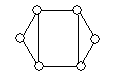

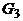
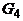
Рис.7
Характеристики графов, которые сохраняются при изоморфизме, называются инвариантами. В этом примере мы видели некоторые простые инварианты – число ребер, набор степеней, число циклов заданной длины, в дальнейшем будут введены еще многие другие. Если удается установить, что для двух исследуемых графов некоторый инвариант принимает разные значения, то эти графы неизоморфны. Изоморфность же двух графов можно доказать, только предъявив соответствующую биекцию.
Графы и матрицы
Пусть G – граф с n вершинами, причем 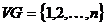 . Построим квадратную матрицу A порядка n, в которой элемент
. Построим квадратную матрицу A порядка n, в которой элемент 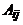 , стоящий на пересечении строки с номером i и столбца с номером j, определяется следующим образом:
, стоящий на пересечении строки с номером i и столбца с номером j, определяется следующим образом:
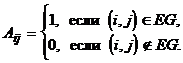
Она называется матрицей смежности графа. Матрицу смежности можно построить и для ориентированного графа, и для неориентированного, и для графа с петлями. Для обыкновенного графа она обладает двумя особенностями: из-за отсутствия петель на главной диагонали стоят нули, а так как граф неориентированный, то матрица симметрична относительно главной диагонали. Обратно, каждой квадратной матрице порядка n, составленной из нулей и единиц и обладающей двумя указанными свойствами, соответствует обыкновенный граф с множеством вершин 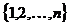 .
.
Другая матрица, ассоциированная с графом – это матрица инцидентности. Для ее построения занумеруем вершины графа числами от 1 до n, а ребра – числами от 1 до m. Матрица инцидентности I имеет n строк и m столбцов, а ее элемент 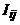 равен 1, если вершина с номером i инцидентна ребру с номером j, в противном случае он равен нулю. На рисунке 8 показан граф с занумерованными вершинами и ребрами и его матрицы смежности и инцидентности.
равен 1, если вершина с номером i инцидентна ребру с номером j, в противном случае он равен нулю. На рисунке 8 показан граф с занумерованными вершинами и ребрами и его матрицы смежности и инцидентности.



Рис. 8
Для ориентированного графа матрица инцидентности определяется несколько иначе: ее элемент 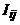 равен 1, если вершина i является началом ребра j, он равен -1, если она является концом этого ребра, и он равен 0, если эта вершина и это ребро не инцидентны друг другу.
равен 1, если вершина i является началом ребра j, он равен -1, если она является концом этого ребра, и он равен 0, если эта вершина и это ребро не инцидентны друг другу.
Взвешенные графы
Часто, особенно когда графы используются для моделирования реальных систем, их вершинам, или ребрам, или и тем и другим приписываются некоторые числа. Природа этих чисел может быть самая разнообразная. Например, если граф представляет собой модель железнодорожной сети, то число, приписанное ребру, может указывать длину перегона между двумя станциями, или наибольший вес состава, который допустим для этого участка пути, или среднее число поездов, проходящих через этот участок в течение суток и т.п. Что бы ни означали эти числа, сложилась традиция называть их весами, а граф с заданными весами вершин и/или ребер – взвешенным графом.
Маршруты, пути, циклы
Маршрут в графе – это последовательность вершин 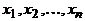 , такая, что для каждого
, такая, что для каждого 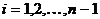 вершины
вершины 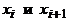 соединены ребром. Эти
соединены ребром. Эти 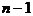 ребер называются ребрами маршрута, говорят, что маршрут проходит через них, а число
ребер называются ребрами маршрута, говорят, что маршрут проходит через них, а число 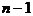 называют длиной маршрута. Говорят, что маршрут соединяет вершины
называют длиной маршрута. Говорят, что маршрут соединяет вершины  , они называются соответственно началом и концом маршрута, вершины
, они называются соответственно началом и концом маршрута, вершины 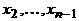 называются промежуточными. Маршрут называется замкнутым, если
называются промежуточными. Маршрут называется замкнутым, если 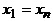 .
.
Путь – это маршрут, в котором все ребра различны. Путь называется простым, если и все вершины в нем различны.
Цикл – это замкнутый путь. Цикл 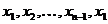 называется простым, если вершины
называется простым, если вершины 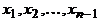 все попарно различны.
все попарно различны.
В графе на рисунке 9 последовательность вершин
2,3,5,4 – не маршрут;
2,3,4,5,1,4,3 – маршрут, но не путь;
3,1,4,5,1,2 – путь, но не простой;
2,3,1,4,3,1,2 – замкнутый маршрут, но не цикл;
2,3,1,4,5,1,2 – цикл, но не простой;
2,3,4,5,1,2 – простой цикл.
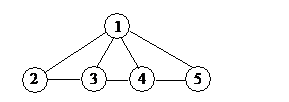
Рис. 9
Установим некоторые простые свойства путей и циклов.
Лемма 1. В любом маршруте, соединяющем две различные вершины, содержится простой путь, соединяющий те же вершины.
Доказательство. Пусть 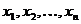 – маршрут. Если все его вершины различны, то это уже простой путь. В противном случае, пусть
– маршрут. Если все его вершины различны, то это уже простой путь. В противном случае, пусть 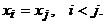 Тогда последовательность
Тогда последовательность 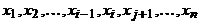 , полученная из этого маршрута удалением отрезка последовательности от
, полученная из этого маршрута удалением отрезка последовательности от 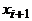 до
до 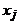 , тоже является маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину. Продолжая действовать таким образом, после конечного числа «спрямлений» получим простой путь, соединяющий
, тоже является маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину. Продолжая действовать таким образом, после конечного числа «спрямлений» получим простой путь, соединяющий  .
.

Лемма 2. Во всяком цикле, проходящем через некоторое ребро, содержится простой цикл, проходящий через это ребро.
Доказательство. Пусть имеется цикл, проходящий через ребро 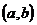 . Если удалить это ребро из графа, то в полученном подграфе останется маршрут, соединяющий a и b. По лемме 1.3 существует простой путь
. Если удалить это ребро из графа, то в полученном подграфе останется маршрут, соединяющий a и b. По лемме 1.3 существует простой путь 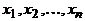 , соединяющий эти вершины, то есть пара
, соединяющий эти вершины, то есть пара 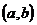 совпадает (как неупорядоченная пара) с парой
совпадает (как неупорядоченная пара) с парой 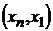 . Но тогда
. Но тогда 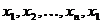 – простой цикл в исходном графе, проходящий через ребро
– простой цикл в исходном графе, проходящий через ребро 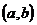 .
.
Отметим, что в формулировке леммы 2 нельзя заменить слово «цикл» словами «замкнутый маршрут». Действительно, если 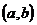 – ребро графа, то последовательность
– ребро графа, то последовательность 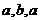 – замкнутый маршрут, проходящий через это ребро, но никакого цикла в нем нет.
– замкнутый маршрут, проходящий через это ребро, но никакого цикла в нем нет.
Лемма 3. Если в графе степень каждой вершины не меньше 2, то в нем есть цикл.
Доказательство. Найдем в графе простой путь наибольшей длины (он существует, так как длина простого пути не может превышать 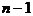 ). Пусть это
). Пусть это 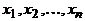 . Вершина
. Вершина 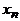 смежна с
смежна с 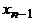 , а так как ее степень не меньше двух, то она смежна еще хотя бы с одной вершиной, скажем, y. Если y была бы отлична от всех вершин пути, то последовательность
, а так как ее степень не меньше двух, то она смежна еще хотя бы с одной вершиной, скажем, y. Если y была бы отлична от всех вершин пути, то последовательность 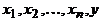 была бы простым путем большей длины. Следовательно, y – это одна из вершин пути,
была бы простым путем большей длины. Следовательно, y – это одна из вершин пути, 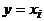 , причем
, причем 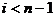 . Но тогда
. Но тогда 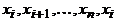 – цикл.
– цикл.
Связность и компоненты
Граф называется связным, если в нем для любых двух вершин имеется маршрут, соединяющий эти вершины. Заметим, что ввиду леммы 1 можно в этом определении заменить слово «маршрут» словами «простой путь».
Для произвольного графа определим на множестве вершин отношение соединимости: вершина a соединима с вершиной b, если существует соединяющий их маршрут. Легко видеть, что это отношение рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности. Классы эквивалентности называются областями связности, а порождаемые ими подграфы – компонентами связности графа. В связном графе имеется только одна компонента связности – весь граф. Компоненты связности можно определить также как максимальные по включению связные подграфы данного графа.
Ребро, при удалении которого увеличивается число компонент связности, называется перешейком.
Лемма 4. Ребро является перешейком в том и только том случае, если через него не проходит никакой цикл.
Доказательство. Если через ребро (a,b) проходит цикл, то после удаления этого ребра вершины a и b останутся соединимыми, значит, число компонент связности не увеличится. Обратно, если после удаления ребра (a,b) число компонент связности не увеличивается, то вершины a и b останутся в одной компоненте, то есть существует соединяющий их маршрут, не проходящий через это ребро. По лемме 1 в нем имеется простой путь x 1, x 2,…, xn, соединяющий a и b, но тогда x 1, x 2,…, xn, x 1– цикл, проходящий через (a,b).
Эйлеровы циклы
Первая теорема теории графов была доказана задолго до того, как стало употребляться словосочетание «теория графов». В 1736 г. появилась работа Эйлера, в которой не только была решена предложенная ему задача о кенигсбергских мостах, но и сформулировано общее правило, позволяющее решить любую задачу такого рода. Интересно, что в одном из писем Эйлер писал по этому поводу: «...это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека...».
На языке теории графов задача состоит в том, чтобы определить, имеется ли в графе путь, проходящий через все его ребра (напомним, что путь, по определению, не может дважды проходить по одному ребру). Такой путь называется эйлеровым путем, а если он замкнут, то эйлеровым циклом. Граф, в котором есть эйлеров цикл, называют эйлеровым графом. В графе, изображенном на рисунке 10а, эйлеров цикл существует, – например, последовательность вершин 1,2,4,5,2,3,5,6,3,1 образует такой цикл. В графе же на рисунке 10б эйлерова цикла нет, но есть эйлеровы пути, например, 2,4,5,2,1,3,5,6,3.
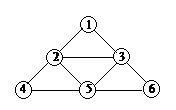
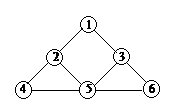
а б
Рис. 10
Рассмотрим сначала условия существования эйлерова цикла в обыкновенном графе. Ясно, что в несвязном графе эйлеров цикл может существовать только в том случае, когда все его ребра принадлежат одной компоненте связности, а все остальные компоненты – просто изолированные вершины. Поэтому достаточно рассматривать связные графы.
Теорема 3. С вязный граф эйлеров тогда и только тогда, когда в нем степени всех вершин четны.
Доказательство. Необходимость условия очевидна, так как при каждом прохождении цикла через какую-либо вершину используются два ребра – по одному из них маршрут входит в вершину, по другому выходит (это относится и к стартовой вершине – в нее ведь придется вернуться). Докажем его достаточность.
Пусть G – связный граф, в котором больше одной вершины и степени всех вершин четны. Значит, степень каждой вершины не меньше 2 и, по лемме 3, в графе G имеется цикл 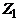 . Если удалить все ребра этого цикла из графа G, то получится граф
. Если удалить все ребра этого цикла из графа G, то получится граф  , в котором степени вершин также четны. Если в
, в котором степени вершин также четны. Если в  нет ни одного ребра, то
нет ни одного ребра, то 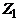 – эйлеров цикл. В противном случае, применяя ту же лемму 3 к графу, полученному из
– эйлеров цикл. В противном случае, применяя ту же лемму 3 к графу, полученному из  удалением всех изолированных вершин, заключаем, что в
удалением всех изолированных вершин, заключаем, что в  имеется цикл
имеется цикл 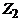 . Удалив из
. Удалив из  все ребра цикла
все ребра цикла 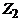 , получим граф
, получим граф 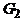 . Продолжая действовать таким образом, пока не придем к пустому графу, получим в итоге систему циклов
. Продолжая действовать таким образом, пока не придем к пустому графу, получим в итоге систему циклов 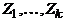 , причем каждое ребро графа принадлежит в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов
, причем каждое ребро графа принадлежит в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов 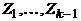 имеет общую вершину с
имеет общую вершину с  . Допустим, для определенности, что таков цикл
. Допустим, для определенности, что таков цикл 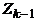 . Пусть
. Пусть 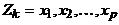 ,
, 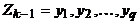 , и
, и 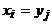 для некоторых i и j. Тогда последовательность вершин
для некоторых i и j. Тогда последовательность вершин
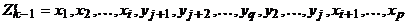
очевидно, является циклом, а множество ребер этого цикла есть объединение множеств ребер циклов 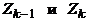 . Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа принадлежит в точности одному из них. Понятно, что продолжая действовать таким образом, в конце концов получим один цикл, который и будет эйлеровым.
. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа принадлежит в точности одному из них. Понятно, что продолжая действовать таким образом, в конце концов получим один цикл, который и будет эйлеровым.
Теперь нетрудно получить и критерий существования эйлерова пути.
Теорема 4. Эйлеров путь в связном графе существует тогда и только тогда, когда в нем имеется не более двух вершин с нечетными степенями.
Доказательство. Если в графе нет вершин с нечетными степенями, то, по предыдущей теореме, в нем имеется эйлеров цикл, он является и эйлеровым путем. Не может быть точно одной вершины с нечетной степенью – это следует из «леммы о рукопожатиях». Если же имеются точно две вершины с нечетными степенями, то построим новый граф, добавив ребро, соединяющее эти вершины. В новом графе степени всех вершин четны и, следовательно, существует эйлеров цикл. Так как циклический сдвиг цикла – тоже цикл, то существует и такой эйлеров цикл, в котором добавленное ребро – последнее. Удалив из этого цикла последнюю вершину, получим эйлеров путь в исходном графе.
Деревья
Центр дерева
Центр графа может состоять из одной вершины (как, например, в графе 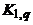 ), а может включать все его вершины (полный граф). Для дерева, как мы увидим, имеется гораздо более ограниченный диапазон возможностей.
), а может включать все его вершины (полный граф). Для дерева, как мы увидим, имеется гораздо более ограниченный диапазон возможностей.
Лемма 6. В дереве для каждой вершины a имеется не более одной смежной с ней вершины b такой, что 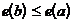 .
.
Доказательство. Пусть x – вершина, наиболее удаленная от a, то есть 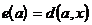 . Единственный путь из a в x проходит через одну из вершин, смежных с a, пусть это вершина b. Если c – другая вершина, смежная с a, то единственный путь из c в x проходит через b и его длина на единицу больше длины пути из a в x. Следовательно,
. Единственный путь из a в x проходит через одну из вершин, смежных с a, пусть это вершина b. Если c – другая вершина, смежная с a, то единственный путь из c в x проходит через b и его длина на единицу больше длины пути из a в x. Следовательно, 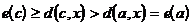 .
.
Теорема 6. Центр дерева состоит из одной вершины или двух смежных вершин.
Доказательство. Допустим, что в некотором дереве существуют две несмежные центральные вершины a и b. Рассмотрим путь, соединяющий эти вершины, и найдем на этом пути промежуточную вершину x с максимальным эксцентриситетом. Так как a и b – вершины с наименьшим эксцентриситетом в дереве, то эксцентриситет x также не меньше эксцентриситета этих вершин. Но тогда оказывается, что 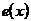 не меньше эксцентриситетов двух смежных с ней вершин – предшествующей ей и следующей за ней на пути, а это противоречит лемме 6. Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин.
не меньше эксцентриситетов двух смежных с ней вершин – предшествующей ей и следующей за ней на пути, а это противоречит лемме 6. Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин.
Двудольные графы
Граф называется двудольным, если множество его вершин можно так разбить на два подмножества, чтобы концы каждого ребра принадлежали разным подмножествам. Эти подмножества называются долями. Таким образом, каждая из долей порождает пустой подграф. Примером двудольного графа является простая цепь 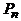 при любом n: одна доля порождается вершинами с четными номерами, другая – с нечетными. Граф
при любом n: одна доля порождается вершинами с четными номерами, другая – с нечетными. Граф 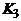 – пример графа, не являющегося двудольным: при любом разбиении множества его вершин на два подмножества в одном из этих подмножеств окажутся две смежных вершины.
– пример графа, не являющегося двудольным: при любом разбиении множества его вершин на два подмножества в одном из этих подмножеств окажутся две смежных вершины.
Теорема 7 (теорема Кенига). Следующие утверждения для графа G равносильны:
(1) G – двудольный граф;
(2) в G нет циклов нечетной длины;
(3) в G нет простых циклов нечетной длины.
Доказательство. (1)Þ(2). Пусть G – двудольный граф, в котором выбрано некоторое разбиение на доли, 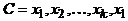 – цикл длины k в графе G. При любом
– цикл длины k в графе G. При любом 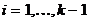 вершины
вершины 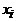 и
и 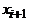 смежны и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит из всех вершин с нечетными индексами, т.е.
смежны и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит из всех вершин с нечетными индексами, т.е. 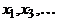 , другая – из всех вершин с четными индексами. Но вершины
, другая – из всех вершин с четными индексами. Но вершины 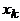 и
и 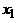 тоже смежны и должны принадлежать разным долям. Следовательно, k – четное число.
тоже смежны и должны принадлежать разным долям. Следовательно, k – четное число.
Импликация (2)Þ(3) очевидна, докажем (3)Þ(1). Рассмотрим граф G, в котором нет простых циклов нечетной длины. Ясно, что граф, в котором каждая компонента связности – двудольный граф, сам двудольный. Поэтому можно считать, что граф G связен. Зафиксируем в нем некоторую вершину a и докажем, что для любых двух смежных между собой вершин x и y имеет место равенство 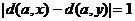 . Действительно, допустим, что
. Действительно, допустим, что 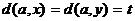 . Пусть
. Пусть 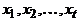 – кратчайший путь из a в x,
– кратчайший путь из a в x, 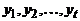 – кратчайший путь из a в y. Эти пути начинаются в одной вершине:
– кратчайший путь из a в y. Эти пути начинаются в одной вершине: 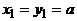 , а оканчиваются в разных:
, а оканчиваются в разных: 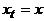 ,
, 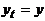 . Поэтому найдется такое k, что
. Поэтому найдется такое k, что 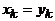 и
и 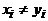 при всех
при всех 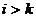 . Но тогда последовательность
. Но тогда последовательность 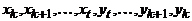 является простым циклом длины
является простым циклом длины 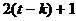 . Следовательно,
. Следовательно, 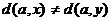 . Предположим, что
. Предположим, что 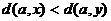 . Если
. Если 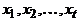 – кратчайший путь из a в x, то, очевидно,
– кратчайший путь из a в x, то, очевидно, 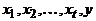 – кратчайший путь из a в y, следовательно,
– кратчайший путь из a в y, следовательно, 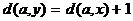 . Итак, расстояния от двух смежных вершин до вершины a различаются ровно не единицу. Поэтому, если обозначить через A множество всех вершин графа, расстояние от которых до вершины a четно, а через B множество всех
. Итак, расстояния от двух смежных вершин до вершины a различаются ровно не единицу. Поэтому, если обозначить через A множество всех вершин графа, расстояние от которых до вершины a четно, а через B множество всех


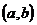 и
и 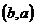 различными. Если да, то говорят, что рассматриваются упорядоченные пары (порядок элементов в паре важен), если нет – неупорядоченные. Если ребро e соединяет вершину a с вершиной b и пара
различными. Если да, то говорят, что рассматриваются упорядоченные пары (порядок элементов в паре важен), если нет – неупорядоченные. Если ребро e соединяет вершину a с вершиной b и пара 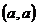 , то есть ребро, соединяющее вершину a с нею же самой, называется петлей. Если такие ребра не допускаются, то говорят, что рассматриваются графы без петель.
, то есть ребро, соединяющее вершину a с нею же самой, называется петлей. Если такие ребра не допускаются, то говорят, что рассматриваются графы без петель.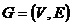 , где V – конечное множество, E – множество неупорядоченных пар различных элементов из V. Элементы множества V называются вершинами графа, элементы множества E – его ребрами.
, где V – конечное множество, E – множество неупорядоченных пар различных элементов из V. Элементы множества V называются вершинами графа, элементы множества E – его ребрами.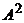 , состоящего из всевозможных упорядоченных пар элементов множества A. Сравнивая с тем, что говорилось выше об определениях различных типов графов, видим, что понятие бинарного отношения эквивалентно понятию ориентированного графа с петлями. Другие типы графов без кратных ребер – это частные виды бинарных отношений. Отношение R называется рефлексивным, если для любого
, состоящего из всевозможных упорядоченных пар элементов множества A. Сравнивая с тем, что говорилось выше об определениях различных типов графов, видим, что понятие бинарного отношения эквивалентно понятию ориентированного графа с петлями. Другие типы графов без кратных ребер – это частные виды бинарных отношений. Отношение R называется рефлексивным, если для любого 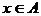 пара (x,x) принадлежит R, и антирефлексивным, если ни одна такая пара не принадлежит R. Оно называется симметричным, если для любых
пара (x,x) принадлежит R, и антирефлексивным, если ни одна такая пара не принадлежит R. Оно называется симметричным, если для любых 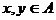 из
из 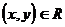 следует
следует 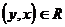 . Обыкновенный граф – не что иное, как антирефлексивное симметричное отношение.
. Обыкновенный граф – не что иное, как антирефлексивное симметричное отношение.


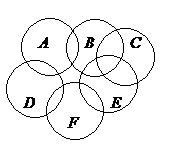
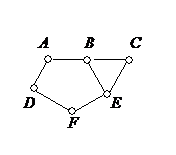
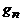 . Эти графы различаются только множествами ребер, а каждое ребро – это неупорядоченная пара различных элементов из V. В комбинаторике такие пары называются сочетаниями из n по 2, их число равно
. Эти графы различаются только множествами ребер, а каждое ребро – это неупорядоченная пара различных элементов из V. В комбинаторике такие пары называются сочетаниями из n по 2, их число равно 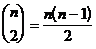 . Каждая пара может быть включена или не включена в множество ребер графа. Применяя правило произведения, приходим к следующему результату.
. Каждая пара может быть включена или не включена в множество ребер графа. Применяя правило произведения, приходим к следующему результату.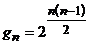 .
.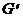 называется подграфом графа G, если
называется подграфом графа G, если 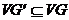 ,
, 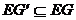 . Всякий подграф может быть получен из графа удалением некоторых вершин и ребер. На рисунке 4 изображены граф G и его подграфы
. Всякий подграф может быть получен из графа удалением некоторых вершин и ребер. На рисунке 4 изображены граф G и его подграфы 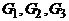 .
.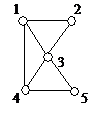
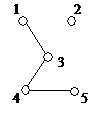
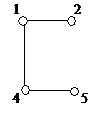
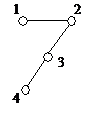

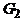
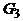
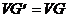 . Остовный подграф может быть получен из графа удалением некоторых ребер, вершины же остаются в неприкосновенности. На рисунке 4
. Остовный подграф может быть получен из графа удалением некоторых ребер, вершины же остаются в неприкосновенности. На рисунке 4  – остовный подграф графа G, а
– остовный подграф графа G, а 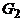 и
и 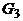 не являются остовными подграфами.
не являются остовными подграфами.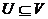 . Рассмотрим подграф
. Рассмотрим подграф 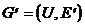 , где
, где 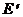 состоит из всех тех ребер графа G, у которых оба конца принадлежат U. Говорят, что этот подграф порожден множеством вершин U. Он обозначается через
состоит из всех тех ребер графа G, у которых оба конца принадлежат U. Говорят, что этот подграф порожден множеством вершин U. Он обозначается через 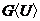 . Порожденный подграф может быть получен из графа удалением «лишних» вершин, т.е. вершин, не принадлежащих U, причем при удалении вершины удаляются и все инцидентные ей ребра.
. Порожденный подграф может быть получен из графа удалением «лишних» вершин, т.е. вершин, не принадлежащих U, причем при удалении вершины удаляются и все инцидентные ей ребра.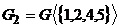 , а подграф
, а подграф 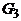 не является ни остовным, ни порожденным.
не является ни остовным, ни порожденным.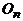 .
.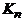 . Граф
. Граф 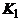 , в частности, имеет одну вершину и ни одного ребра.
, в частности, имеет одну вершину и ни одного ребра.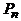 – граф с множеством вершин {1,2,..., n } и множеством ребер
– граф с множеством вершин {1,2,..., n } и множеством ребер 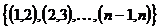 .
.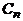 – граф, который получается из
– граф, который получается из 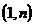 .
.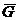 , у которого множество вершин то же, что у G, и две различные вершины смежны тогда и только тогда, когда они не смежны в G. Например,
, у которого множество вершин то же, что у G, и две различные вершины смежны тогда и только тогда, когда они не смежны в G. Например, 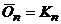 . Другой пример показан на рисунке 5. Очевидно, всегда
. Другой пример показан на рисунке 5. Очевидно, всегда 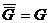 .
.

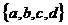 . При внимательном рассмотрении можно обнаружить, что это разные графы – в левом имеется ребро
. При внимательном рассмотрении можно обнаружить, что это разные графы – в левом имеется ребро 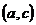 , в правом же такого нет. В то же
, в правом же такого нет. В то же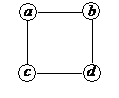
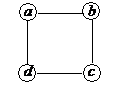
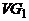 на множество
на множество 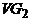 , что
, что 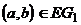 тогда и только тогда, когда
тогда и только тогда, когда 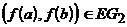 . Отображение f в этом случае называется изоморфизмом
. Отображение f в этом случае называется изоморфизмом 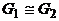 .
.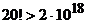 ). Однако для многих конкретных пар графов их неизоморфность устанавливается довольно легко. Рассмотрим, например, графы, изображенные на рисунке 7. Так как при изоморфизме пара смежных вершин переходит в пару смежных, а пара несмежных – в пару несмежных, то ясно, что число ребер у двух изоморфных графов должно быть одинаковым. Поэтому сразу можно сказать, что графы
). Однако для многих конкретных пар графов их неизоморфность устанавливается довольно легко. Рассмотрим, например, графы, изображенные на рисунке 7. Так как при изоморфизме пара смежных вершин переходит в пару смежных, а пара несмежных – в пару несмежных, то ясно, что число ребер у двух изоморфных графов должно быть одинаковым. Поэтому сразу можно сказать, что графы  дело обстоит немного сложнее – у них и наборы степеней одинаковы. Все же и эти графы неизоморфны: можно заметить, что в
дело обстоит немного сложнее – у них и наборы степеней одинаковы. Все же и эти графы неизоморфны: можно заметить, что в 



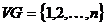 . Построим квадратную матрицу A порядка n, в которой элемент
. Построим квадратную матрицу A порядка n, в которой элемент 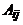 , стоящий на пересечении строки с номером i и столбца с номером j, определяется следующим образом:
, стоящий на пересечении строки с номером i и столбца с номером j, определяется следующим образом: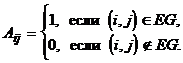
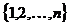 .
.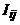 равен 1, если вершина с номером i инцидентна ребру с номером j, в противном случае он равен нулю. На рисунке 8 показан граф с занумерованными вершинами и ребрами и его матрицы смежности и инцидентности.
равен 1, если вершина с номером i инцидентна ребру с номером j, в противном случае он равен нулю. На рисунке 8 показан граф с занумерованными вершинами и ребрами и его матрицы смежности и инцидентности.


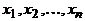 , такая, что для каждого
, такая, что для каждого 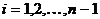 вершины
вершины 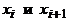 соединены ребром. Эти
соединены ребром. Эти 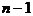 ребер называются ребрами маршрута, говорят, что маршрут проходит через них, а число
ребер называются ребрами маршрута, говорят, что маршрут проходит через них, а число  , они называются соответственно началом и концом маршрута, вершины
, они называются соответственно началом и концом маршрута, вершины 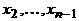 называются промежуточными. Маршрут называется замкнутым, если
называются промежуточными. Маршрут называется замкнутым, если 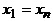 .
.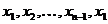 называется простым, если вершины
называется простым, если вершины 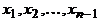 все попарно различны.
все попарно различны.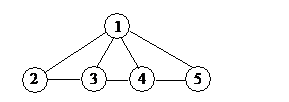
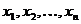 – маршрут. Если все его вершины различны, то это уже простой путь. В противном случае, пусть
– маршрут. Если все его вершины различны, то это уже простой путь. В противном случае, пусть 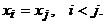 Тогда последовательность
Тогда последовательность 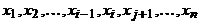 , полученная из этого маршрута удалением отрезка последовательности от
, полученная из этого маршрута удалением отрезка последовательности от 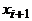 до
до 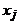 , тоже является маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину. Продолжая действовать таким образом, после конечного числа «спрямлений» получим простой путь, соединяющий
, тоже является маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину. Продолжая действовать таким образом, после конечного числа «спрямлений» получим простой путь, соединяющий 
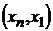 . Но тогда
. Но тогда 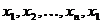 – простой цикл в исходном графе, проходящий через ребро
– простой цикл в исходном графе, проходящий через ребро 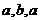 – замкнутый маршрут, проходящий через это ребро, но никакого цикла в нем нет.
– замкнутый маршрут, проходящий через это ребро, но никакого цикла в нем нет.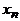 смежна с
смежна с 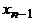 , а так как ее степень не меньше двух, то она смежна еще хотя бы с одной вершиной, скажем, y. Если y была бы отлична от всех вершин пути, то последовательность
, а так как ее степень не меньше двух, то она смежна еще хотя бы с одной вершиной, скажем, y. Если y была бы отлична от всех вершин пути, то последовательность 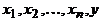 была бы простым путем большей длины. Следовательно, y – это одна из вершин пути,
была бы простым путем большей длины. Следовательно, y – это одна из вершин пути, 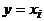 , причем
, причем 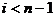 . Но тогда
. Но тогда 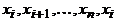 – цикл.
– цикл. 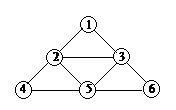
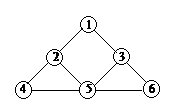
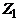 . Если удалить все ребра этого цикла из графа G, то получится граф
. Если удалить все ребра этого цикла из графа G, то получится граф 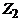 . Удалив из
. Удалив из 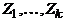 , причем каждое ребро графа принадлежит в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов
, причем каждое ребро графа принадлежит в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов 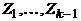 имеет общую вершину с
имеет общую вершину с  . Допустим, для определенности, что таков цикл
. Допустим, для определенности, что таков цикл 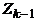 . Пусть
. Пусть 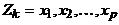 ,
, 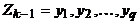 , и
, и 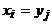 для некоторых i и j. Тогда последовательность вершин
для некоторых i и j. Тогда последовательность вершин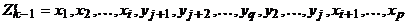
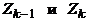 . Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа принадлежит в точности одному из них. Понятно, что продолжая действовать таким образом, в конце концов получим один цикл, который и будет эйлеровым.
. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа принадлежит в точности одному из них. Понятно, что продолжая действовать таким образом, в конце концов получим один цикл, который и будет эйлеровым. 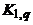 ), а может включать все его вершины (полный граф). Для дерева, как мы увидим, имеется гораздо более ограниченный диапазон возможностей.
), а может включать все его вершины (полный граф). Для дерева, как мы увидим, имеется гораздо более ограниченный диапазон возможностей.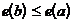 .
.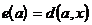 . Единственный путь из a в x проходит через одну из вершин, смежных с a, пусть это вершина b. Если c – другая вершина, смежная с a, то единственный путь из c в x проходит через b и его длина на единицу больше длины пути из a в x. Следовательно,
. Единственный путь из a в x проходит через одну из вершин, смежных с a, пусть это вершина b. Если c – другая вершина, смежная с a, то единственный путь из c в x проходит через b и его длина на единицу больше длины пути из a в x. Следовательно, 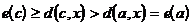 .
. 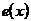 не меньше эксцентриситетов двух смежных с ней вершин – предшествующей ей и следующей за ней на пути, а это противоречит лемме 6. Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин.
не меньше эксцентриситетов двух смежных с ней вершин – предшествующей ей и следующей за ней на пути, а это противоречит лемме 6. Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин. 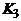 – пример графа, не являющегося двудольным: при любом разбиении множества его вершин на два подмножества в одном из этих подмножеств окажутся две смежных вершины.
– пример графа, не являющегося двудольным: при любом разбиении множества его вершин на два подмножества в одном из этих подмножеств окажутся две смежных вершины.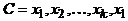 – цикл длины k в графе G. При любом
– цикл длины k в графе G. При любом 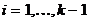 вершины
вершины 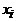 и
и 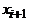 смежны и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит из всех вершин с нечетными индексами, т.е.
смежны и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит из всех вершин с нечетными индексами, т.е. 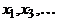 , другая – из всех вершин с четными индексами. Но вершины
, другая – из всех вершин с четными индексами. Но вершины 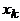 и
и 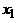 тоже смежны и должны принадлежать разным долям. Следовательно, k – четное число.
тоже смежны и должны принадлежать разным долям. Следовательно, k – четное число.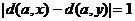 . Действительно, допустим, что
. Действительно, допустим, что 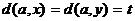 . Пусть
. Пусть 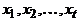 – кратчайший путь из a в x,
– кратчайший путь из a в x, 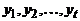 – кратчайший путь из a в y. Эти пути начинаются в одной вершине:
– кратчайший путь из a в y. Эти пути начинаются в одной вершине: 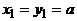 , а оканчиваются в разных:
, а оканчиваются в разных: 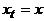 ,
, 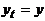 . Поэтому найдется такое k, что
. Поэтому найдется такое k, что 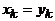 и
и 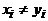 при всех
при всех 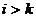 . Но тогда последовательность
. Но тогда последовательность 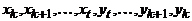 является простым циклом длины
является простым циклом длины 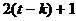 . Следовательно,
. Следовательно, 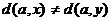 . Предположим, что
. Предположим, что 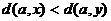 . Если
. Если 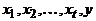 – кратчайший путь из a в y, следовательно,
– кратчайший путь из a в y, следовательно, 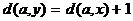 . Итак, расстояния от двух смежных вершин до вершины a различаются ровно не единицу. Поэтому, если обозначить через A множество всех вершин графа, расстояние от которых до вершины a четно, а через B множество всех
. Итак, расстояния от двух смежных вершин до вершины a различаются ровно не единицу. Поэтому, если обозначить через A множество всех вершин графа, расстояние от которых до вершины a четно, а через B множество всех