Определение 1. СВ
где X ~ N (m, σ), имеет логарифмически нормальное (логнормальное) распределение с параметрами m и σ > 0.
Замечание 1. Так как ex - строго возрастающая функция, то, учитывая вид нормального распределения (определение Л6.Р1.О1), найдём плотность логнормального распределения
| fY (y)
|
| 4)f(x) =
| fx (ψ (y)) ψ '(y) =
| |
| ψ (y) = ln yψ '(y) = 1/ y
| |
| =
|
| =
| {
| |
yσ √2 π
|
| exp
| {
| -
| (ln y - m)2
2 σ 2
| }
| 0,
| , y > 0, y ≤ 0.
|
График fY (y) (см. рис. 8) асимметричен с максимумом в точке y = exp(m - σ 2).

Рисунок 8.
Замечание 2. Найдём МО и дисперсию СВ Y. По определению:
| M[ Y ] =
| 1
σ √2 π
|
| +∞ ∫ 0
| exp{-(ln y - m)2/2 σ 2} d y =
| |
| замена перем. y = exp{ σ (t + σ) + m }
| |
| =
|
| =
| exp{ m + σ 2/2}
√2 π
|
| +∞ ∫ -∞
| e-t
| 2
| /2 d t = exp{ m + σ 2/2}.
|
Аналогично можно найти M [ Y 2]= exp{2(σ 2 + m)}. Поэтому
D [ Y ] = M [ Y 2] - (M [ Y ])2 = exp(σ 2 + 2 m)*(exp{ σ 2} - 1).
Замечание 3. Логнормальное распределение широко используется в экономической статистике, статистической физике и др.
Экспоненциальное распределение.
Определение 1. СВ X имеет экспоненциальное (показательное) распределение с параметром λ > 0 (X ~ E (λ)), если (см. рис. 3)
| f (x)=
| {
| λe-λx 0
| ,,
| если x ≥ 0, если x < 0.
|

Рисунок 3 Рисунок 4.
Замечание 1. Функция распределения СВ X ~ E (λ) равна (см. рис. 4): F (x) = 0, если x < 0, и
| F (x)
| Δ =
| x ∫ -∞
| f (x) d x = | f (x) = 0,если x < 0 | = λ
| x ∫ 0
| e-λx d x = 1 - e-λx, x ≥ 0.
|
Замечание 2. Характеристическая функция СВ X ~ Е (λ):
| g (t)
| Δ =
| +∞ ∫ -∞
| eitxf (x) d x = λ
| +∞ ∫ 0
| e-λxeitx d x = λ
| +∞ ∫ 0
| ex (it - λ) d x =
|
| =
|
| λ
it-λ
| ex (it-λ)
| |
| +∞ x =0
| =
| λ
λ-it
| .
|
Замечание 3. Найдём МО и дисперсию СВ X ~ E (λ):
| mx
| Δ =
| ν 1 =
| 1
i
| d
d t
| g (t)
| |
| t =0
| =
| λ
(λ-it)2
| |
| t =0
| =
| 1
λ
| ,
|
| ν 2 =
| 1
i 2
| d2
d t 2
| g (t)
| |
| t =0
| =
| 2 λ
(λ-it)3
| |
| t =0
| =
| 2
λ 2
| ,
|
| dx
| 6)mx =
| ν 2 - ν 12 =
| 1
λ 2
| .
|
Замечание 4. Экспоненциальное распределение является одним из основных распределений, используемых в теории надежности. Например, продолжительность безотказной работы многих технических устройств, а также время задержки вылета самолёта по вине технических служб аэропорта удовлетворительно описываются соответствующими экспоненциальными распределениями.
Закон больших чисел.
Под законом больших чисел в теории вероятностей понимают совокупность теорем, в которых утверждается, что существует связь между средним арифметическим достаточно большого числа случайных величин и средним арифметическим их математических ожиданий.
12.Неравенство Чебышёва. теорема Чебышева. Лемма Чебышева (Маркова). Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание М(Х), то для любого a>0 имеет место неравенство:

| (2.14.1)
|
12.Неравенство Чебышева. Если случайная величина Х имеет математическое ожидание М(Х) и дисперсию D(X), то для любого e>0 имеет место неравенство:

| (2.14.2)
|
Неравенство Чебышева является в теории вероятностей общим фактом и позволяет оценить нижнюю границу вероятностей.
12.Теорема. Закон больших чисел Чебышева. Пусть Х1, Х2,..., Хn - последовательность попарно независимых случайных величин, имеющих конечные математические ожидания и дисперсии, ограниченные сверху постоянной C=const (D(Xi) £ C(i=1, 2,..., n)). Тогда для любого e>0:

| (2.14.3)
|
Теорема показывает, что среднее арифметическое большого числа случайных величин с вероятностью сколь угодно близкой к 1 будет мало отклониться от среднего арифметического математических ожиданий.
Следствие 1. Если вероятность наступления события А в каждом из n независимых испытаний равна p, m - число наступлений события А в серии из n независимых испытаний, то, каково бы ни было число e > 0 имеет место предел:
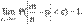
| (2.14.4)
|
Таким образом устанавливается связь между относительной частотой появления события А и постоянной вероятностью p в серии из n независимых испытаний.
Следствие 2. Теорема Пуассона. Если в последовательности независимых испытаний вероятность появления события А в k-ом испытании равна pk, то
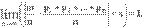 где m-число появлений события А в серии из n испытаний.
где m-число появлений события А в серии из n испытаний.
Следствие 3. Теорема Бернулли. Если Х1, Х2,..., Хn - последовательность независимых случайных величин таких, что
М(Х1)=М(Х2) =... = М(Хn)=а,
М(Х1)<C, D(X2)<C,..., D(Xn)<C, где С=const,
то, каково бы ни было постоянное число e > 0 имеет место предел:

| (2.14.5)
|
Этот частный случай закона больших чисел позволяет обосновать правило средней арифметической.
Законы больших чисел не позволяют уменьшить неопределенность в каждом конкретном случае, они утверждают лишь о существовании закономерности при достаточно большом числе опытов. Например, если при подбрасывании монеты 10 раз появился герб, то это не означает, что в 11 раз появится цифра.

Правило трех сигм.
Если случайная величина X распределена нормально (с параметрами а и  ), то практически достоверно, что абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т.е.
), то практически достоверно, что абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т.е. 
Другими словами, если случайная величина X имеет нормальный закон распределения с параметрами а и  , то практически достоверно, что её значения заключены в интервале
, то практически достоверно, что её значения заключены в интервале 
Воспользуемся
Вероятность того, что отклонение случайной величины X, распределённой по нормальному закону, от математического ожидания а не превысит по абсолютной величине величину  равна
равна

Доказательство.

Из последнего равенства можно сделать вывод о том, что нарушение "правила трёх сигм", т.е. отклонение нормально распределённой случайной величины X больше, чем на  (по абсолютной величине), является событием практически невозможным, так как его вероятность достаточно мала:
(по абсолютной величине), является событием практически невозможным, так как его вероятность достаточно мала:

Теорема Бернулли.
Определение 1. Числом сочетаний Cnm из n элементов по m (m ≤ n) называется количество всех возможных способов, которыми можно выбрать m различных элементов из n, вычисляемое по формуле:
Теорема 1. Пусть опыт G производится независимо n раз в одних и тех же условиях, причем некоторое событие A при каждом повторении опыте появляется с одной и той же вероятностью p = P (A). Тогда вероятность Pn (m) события Bn (m), состоящего в том, что при n повторениях опыта G событие A произойдет ровно m раз, вычисляется по формуле Бернулли:
| Pn (m)
| Δ =
| P(Bn (m)) = Cnm pm (1- p) n-m.
|
Замечание 1. Проверим справедливость этой формулы для n = 3 и m = 1. В этом случае
| P3(1)
| Δ =
| P(B 3(1)) = C 31 p 1(1- p)2 = 3 p (1 - p) 2.
|
Представим событие B 3(1) в виде суммы трёх несовместных событий:
| B 3(1) = A 1 A 2 A 3 + A 1 A 2 A 3 + A 1 A 2 A 3,
|
где события Ai и Ai состоят в том, что событие A произойдёт или не произойдёт в i -м опыте, i = 1,2,3. Поэтому по замечанию Л3.Р2.З2:
| P 3(1)
| Δ =
| P(B 3(1)) = P(A 1 A 2 A 3) + P(A 1 A 2 A 3) + P(A 1 A 2 A 3).
|
Так как события A 1, A 2, A 3, а так же A 1, A 2, A 3 независимы, то
| P 3(1) = P(A 1)P(A 2)P(A 3) + P(A 1)P(A 2)P(A 3) + P(A 1)P(A 2)P(A 3).
|
Поэтому P 3(1) = 3 p (1 - p)2. В общем случае формуле Бернулли доказывается аналогично.
Пример 1. Монету бросают 5 раз. Найти вероятность того, что "герб" выпадет ровно три раза. В этом случае
| n = 5, m = 3, p = 1/2, q
| Δ =
| 1 - p = 1/2.
|
Тогда по формуле Бернулли
P 5(3) = C 53 (1/2)3(1/2)2 = 5/16.








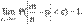
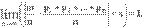 где m-число появлений события А в серии из n испытаний.
где m-число появлений события А в серии из n испытаний.

 ), то практически достоверно, что абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т.е.
), то практически достоверно, что абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т.е. 
 , то практически достоверно, что её значения заключены в интервале
, то практически достоверно, что её значения заключены в интервале 
 равна
равна

 (по абсолютной величине), является событием практически невозможным, так как его вероятность достаточно мала:
(по абсолютной величине), является событием практически невозможным, так как его вероятность достаточно мала:



