

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
291. Квадратичные формы и их матрицы.
Квадратичной формой n действительных переменных  называется выражение
называется выражение
 (1)
(1)
где вещественные числа  называются коэффициентами квадратичной формы.
называются коэффициентами квадратичной формы.
Квадратичную форму (1) всегда можно представить так, чтобы коэффициенты при 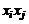 и
и 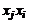 были равны между собой. Действительно, имеем
были равны между собой. Действительно, имеем
 .
.
Поэтому в дальнейшем будем считать, что в квадратичной форме (1)
 . (2)
. (2)
Из коэффициентов квадратичной формы составим симметрическую матрицу
 , (3)
, (3)
которую назовем матрицей квадратичной формы.
Обратно, всякой симметрической матрице (3) соответствует единственная квадратичная форма (1) с точностью до обозначения переменных  .
.
Рангом r квадратичной формы называют ранг ее матрицы. Квадратичная форма n переменных (1) называется невырожденной, если ее матрица А – невырождена, т.е.  , и вырожденной, если
, и вырожденной, если  .
.
Запишем квадратичную форму в матричном виде. Пусть  – столбец, тогда
– столбец, тогда  – строка. Имеем
– строка. Имеем
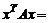
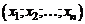


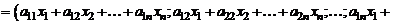
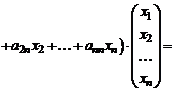
 , т.е.
, т.е.  (1΄)
(1΄)
В квадратичной форме (1΄) перейдем к новым переменным 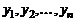 по формулам
по формулам
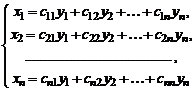
или в матричной форме
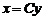 , (4)
, (4)
где 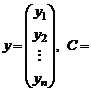
 .
.
Тогда получим квадратичную форму  n переменных
n переменных 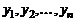 с некоторой матрицей В. В этом случае говорят, что квадратичная форма
с некоторой матрицей В. В этом случае говорят, что квадратичная форма  переводится в квадратичную форму
переводится в квадратичную форму  линейным однородным преобразованием (4).
линейным однородным преобразованием (4).
Две квадратичные формы называют конгруэнтными, если существует невырожденное линейное однородное преобразование, переводящее одну из них в другую.
Определим вид матрицы В квадратичной формы  , в которую переходит квадратичная форма
, в которую переходит квадратичная форма  при преобразовании (4). Подставляя (4) в (1’), получим
при преобразовании (4). Подставляя (4) в (1’), получим

 .
.
Так как

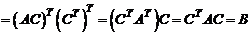 ,
,
то В – симметрическая матрица. Значит,  является матрицей квадратичной формы
является матрицей квадратичной формы  .
.
292. Приведение квадратичной формы к каноническому виду.
|
|
10. Канонические и нормальные квадратичные формы. Квадратичная форма  называется канонической, если она не содержит произведений различных переменных, т.е. имеет вид
называется канонической, если она не содержит произведений различных переменных, т.е. имеет вид
 , (1)
, (1)
где 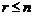 .
.
Каноническая квадратичная форма называется нормальной,
если  , т.е. отличные от нуля коэффициенты при квадратах переменных равны +1 или –1.
, т.е. отличные от нуля коэффициенты при квадратах переменных равны +1 или –1.
Например, квадратичная форма 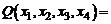
 , для которой
, для которой  , имеет канонический вид; квадратичная форма
, имеет канонический вид; квадратичная форма 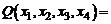
 имеет нормальный вид, так как
имеет нормальный вид, так как  ,
,  .
.
Теорема 1. Любая квадратичная форма
 (2)
(2)
невырожденным преобразованием может быть приведена к каноническому виду.
Следствие 1. Любую квадратичную форму (2) линейным невырожденным преобразованием можно привести к нормальному виду.
30. Приведение квадратичной формы к каноническому виду ортогональным преобразованием. Покажем, что квадратичную форму (2) можно привести к каноническому виду.
Приведение квадратичной формы к каноническому виду можно осуществить с помощью преобразования
 , (14)
, (14)
где в (14) Т – матрица, приводящая матрицу А квадратичной формы к диагональному виду; 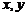 - векторы размерности n.
- векторы размерности n.
Столбцами матрицы Т служат ортонормированные собственные векторы матрицы А.
Отметим также, что в этом случае преобразование 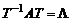 превращается в преобразование
превращается в преобразование  и отпадает необходимость находить обратную матрицу
и отпадает необходимость находить обратную матрицу  .
.
40. Любая квадратичная форма может быть приведена к каноническому виду невырожденным преобразованием.
293. Знакоопределённые квадратичные формы.
20. Знакоопределенные квадратичные формы. Квадратичная форма (2) называется положительно определенной, если она приводится к нормальному виду, состоящему из n положительных квадратов, т.е.
 ,
,
где
 . (6)
. (6)
Утверждение 1. Квадратичная форма (2) является положительно определенной тогда и только тогда, когда она принимает положительные значения при любой ненулевой системе значений переменных  .
.
Главными минорами квадратичной формы (2) называют миноры порядка  ее матрицы А, расположенные в левом верхнем углу, т.е. числа
ее матрицы А, расположенные в левом верхнем углу, т.е. числа
|
|
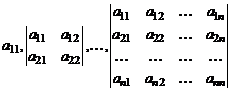 . (7)
. (7)
Квадратичная форма (2) называется отрицательно определенной, если она является невырожденной и приводится к нормальному виду, содержащему только отрицательные квадраты всех переменных.
Положительно определенные и отрицательно определенные квадратичные формы называют знакоопределенными квадратичными формами.
Вырожденные квадратичные формы, нормальный вид которых состоит из квадратов переменных одного знака, называют полуопределенными (соответственно неотрицательными, неположительными).
Неопределенными называют квадратичные формы, нормальный вид которых содержит как положительные так и отрицательные квадраты переменных.
294. Условия знакоопределённости квадратичных форм.
Теорема 2 (критерий Сильвестра). Квадратичная форма (2) является положительно определенной тогда и только тогда, когда все ее главные миноры (7) положительны.
|
|
|

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!