

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Недостаточность «классического» подхода к вероятности, основанного на конечной группе равновозможных элементарных событий, отмечалась ещё в начале развития теории вероятностей. Для ряда практических задач требовалось построение понятия «вероятности»и в том случае, когда число исходов испытания было бесконечным. Например, вероятность попадания в цель при орудийной стрельбе, вероятность выигрыша в некоторых «геометрических» играх.
Расширение понятия «вероятности»в такого рода испытаниях сводится к следующему.
Пусть точка бросается наудачу в интервал [ a; b ]. Внутри этого интервала выделен другой – [ c; d ] (рис.4.5.1). Естественно предположить, что вероятность попадания точки в этот интервал пропорциональна его длине, т.е. чем больше интервал, тем вероятнее в него попадание точки. Можно также предположить, что вероятность не зависит от того, где находится этот интервал, т.е. вероятности попадания в разные интервалы одинаковой длины совпадают.
|
 ,
,
Рис.4.5.1
т.е. вероятность того, что брошенная в [ a; b ] точка M попадет в [ c; d ], равна отношению длин этих отрезков.
 Аналогичным образом определяют вероятность того, что точка, брошенная в область G, попадет в область g (рис.4.5.2):
Аналогичным образом определяют вероятность того, что точка, брошенная в область G, попадет в область g (рис.4.5.2):
 ,
,
Рис.4.5.2
т.е. вероятность такого события равна отношению площадей этих областей.
 Пример 1. Рассмотрим мишень; изображённую на рис.4.5.3. Пусть круг имеет радиус R м и каждый выстрел обязательно попадает внутрь круга. Тогда вероятность попасть в треугольник равна отношению площадей треугольника и круга. Площадь круга равна
Пример 1. Рассмотрим мишень; изображённую на рис.4.5.3. Пусть круг имеет радиус R м и каждый выстрел обязательно попадает внутрь круга. Тогда вероятность попасть в треугольник равна отношению площадей треугольника и круга. Площадь круга равна  . Сторона правильного треугольника, вписанного в круг, равна
. Сторона правильного треугольника, вписанного в круг, равна  , а высота
, а высота  . Площадь равностороннего треугольника, вписанного в круг, равна
. Площадь равностороннего треугольника, вписанного в круг, равна  , где а – сторона треугольника. Следовательно, площадь треугольника равна
, где а – сторона треугольника. Следовательно, площадь треугольника равна  , а вероятность попадания в треугольник –
, а вероятность попадания в треугольник –  , что приблизительно равно 0,41.
, что приблизительно равно 0,41.
|
|
Пример 2. Игра «монета в квадрате» заключается в следующем:

| 
|
| Рис.4.5.4 | Рис. 4.5.5 |
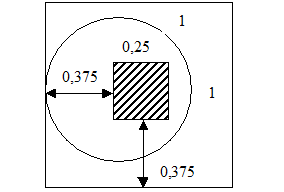
Игрок бросает монету диаметром 0,75 дюйма с большого расстояния на стол, разграфленный на квадраты со стороной в один дюйм (один дюйм» 2.54 см). Если монета попадает внутрь любого квадрата, то игрок получает награду, если монета пересекает границу квадратов, то он теряет монету (рис.4.5.4). Какую награду должен назначить хозяин стола, чтобы не «прогореть»?
Рассмотрим попадание в один квадрат. Пространство элементарных событий, соответствующее этому испытанию, состоит из упорядоченных пар чисел – координат центра монеты. Это пространство непрерывно и бесконечно.
Достаточно рассмотреть лишь попадание в один квадрат. Т.к. радиус монеты равен 0,375 дюйма, то для выигрыша игрока надо, чтобы центр монеты попал в заштрихованный квадрат со стороной 0,25 дюйма (рис.4.5.5).
Тогда вероятность выигрыша игрока равна отношению площадей квадратов, а т.к. площадь внешнего квадрата равна 1, то эта вероятность равна 0,252, или 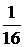 . Следовательно, игрок выигрывает в среднем один раз из 16. Если награда будет установлена меньше 16 монет, например, 10 монет, то хозяин никогда не будет оставаться в проигрыше.
. Следовательно, игрок выигрывает в среднем один раз из 16. Если награда будет установлена меньше 16 монет, например, 10 монет, то хозяин никогда не будет оставаться в проигрыше.
Тема: Сложение и умножение вероятностей
5. Сложение и умножение вероятностей
Схема равновозможных исходов позволяет вычислить вероятности простых событий. Чтобы вычислять вероятности более сложных событий, применяются правила сложения и умножения вероятностей.
Сложение вероятностей
1. Для двух несовместных событий Р (А+В) =Р (А) +Р (В).
2. Для вычисления вероятности суммы нескольких попарно несовместных событий (больше двух) используется аксиома 3, т.е. свойство аддитивности вероятности:
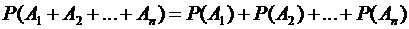 .
.
При этом весьма полезным является понятие противоположного события.
|
|
Пример. Круговая мишень состоит из трёх зон (рис.5.1.1). Вероятность попадания в 1-ю зону при одном выстреле равна 0,15; во 2-ю – 0,23; в 3-ю – 0,17. Найти вероятность промаха при одном выстреле.
|
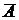 - промах по всей мишени. Обозначим попадание в мишень А, а
- промах по всей мишени. Обозначим попадание в мишень А, а  - попадания соответственно в 1-ю, 2-ю и 3-ю зоны – попарно несовместные события. Очевидно, что
- попадания соответственно в 1-ю, 2-ю и 3-ю зоны – попарно несовместные события. Очевидно, что  . В случае попадания на границы кругов будем считать, что попали в круг ближе к центру. По аксиоме 3
. В случае попадания на границы кругов будем считать, что попали в круг ближе к центру. По аксиоме 3

Рис.5.1.1
3. Для бесконечного числа попарно несовместных событий
 .
.
Здесь бесконечные суммы надо понимать как суммы рядов.
4. Если два события А и Всовместны, то для нахождения вероятности их суммы применяется следствие 6 из системы аксиом (формула (3.2.10)):
Р (А+В) =Р (А) +Р (В) -Р (АВ). (5.1.1)
5. Вероятность суммы трёх совместных событий вычисляется по формуле:
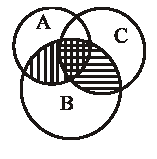
Р (А+В+С) =Р (А) +Р (В) +Р (С) -Р (АВ) -Р (АС) -Р (ВС) +Р (АВС). (5.1.2)
Доказательство.
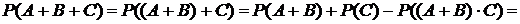


 =
=  , ч.т.д.
, ч.т.д.
Рис.5.1.2 показывает справедливость замены произведения  на АВС.
на АВС.
Рис.5.1.2
|
|
|

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!