

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:F¢(x) = f(x).
первообразных для одной и той же функции м.б. бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.F1(x) = F2(x) + C.
Неопределенный интеграл. Неопред.интегралом ф-ии f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 
Ус-ем сущ-я неопред.интеграла на некотором отрезке явл-ся непрерывность ф-ии на этом отрезке.
Св-ва: 1.) 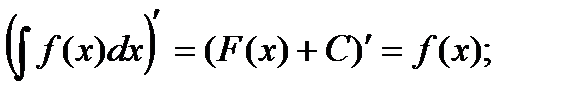 2.)
2.)  3)
3) 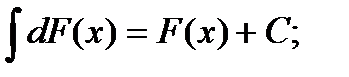
4.)  где u, v, w – некоторые функции от х, 5)
где u, v, w – некоторые функции от х, 5) 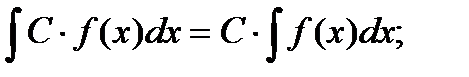
Таблица неопред.интегр.:
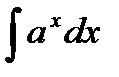 =
= 
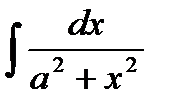 =
= 
 =
= 
 =ln
=ln 
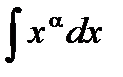 =
= 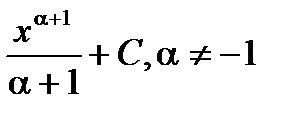
 = ex + C
= ex + C
 =sinx + C
=sinx + C
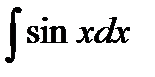 = -cosx + C
= -cosx + C
 = tgx + C
= tgx + C
 = -ctgx + C
= -ctgx + C
 = arcsin
= arcsin 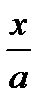 + C
+ C
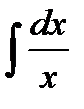 =
= 
Неопределенный интеграл и его св-ва.
Неопред.интегралом ф-ии f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 
Ус-ем сущ-я неопред.интеграла на некотором отрезке явл-ся непрерывность ф-ии на этом отрезке.
Св-ва: 1.) 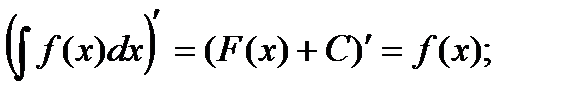 2.)
2.)  3)
3) 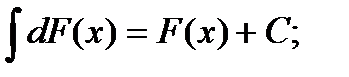
4.)  где u, v, w – некоторые функции от х. 5)
где u, v, w – некоторые функции от х. 5) 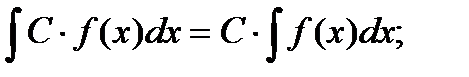
Таблица неопред.интегр.:
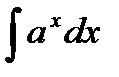 =
= 
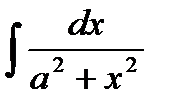 =
= 
 =
= 
 =ln
=ln 
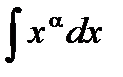 =
= 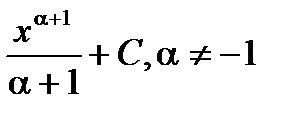
 = ex + C
= ex + C
 =sinx + C
=sinx + C
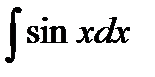 = -cosx + C
= -cosx + C
 = tgx + C
= tgx + C
 = -ctgx + C
= -ctgx + C
 = arcsin
= arcsin 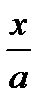 + C
+ C
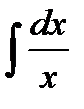 =
= 
39. Интегралы от основных элементарных функций
значения неопределенных интегралов большинства элементарных ф-ий: 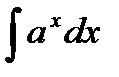 =
= 
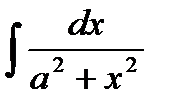 =
= 
 =
= 
 =ln
=ln 
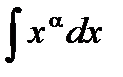 =
= 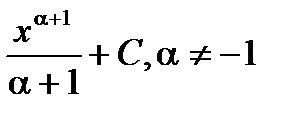
 = ex + C
= ex + C
 =sinx + C
=sinx + C
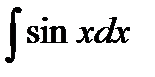 = -cosx + C
= -cosx + C
 = tgx + C
= tgx + C
 = -ctgx + C
= -ctgx + C
 = arcsin
= arcsin 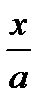 + C
+ C
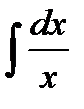 =
= 
Метод замены переменных.
Если требуется найти интеграл  , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:

Пример. Найти неопределенный интеграл  .
.
Сделаем замену t = sinx, dt = cosxdt.

Интегрирование по частям.
Способ основан на формуле производной произведения:(uv)¢ = u¢v + v¢u, где u и v – некоторые функции от х.
|
|
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем:  ,
,
Формула интегрир-я по частям: 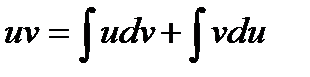 или
или 
Пример. 


Определенный интеграл.
Определенным интегралом от ф-и 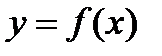 на
на 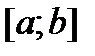 наз-тся конечный предел её интегральной суммы, когда число элемент. отрезков неограниченно возрастает, а длина наиб. из них стремится к нулю. Обозначается:
наз-тся конечный предел её интегральной суммы, когда число элемент. отрезков неограниченно возрастает, а длина наиб. из них стремится к нулю. Обозначается: 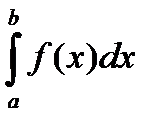
Число a называется нижним пределом интегрирования, b- верхним пределом интегрирования, f(x)- подинтегральной ф-ей, х-переменной интегрирования.
По определению
 (1)
(1)
след-но величина определенного интеграла не зависит от переменной интегрирования, т.е.
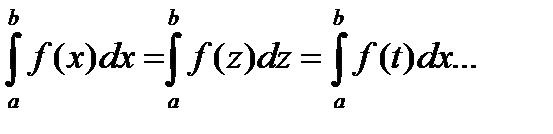
Ф-я, для к-рой существует предел (1) наз-тся интегрированием на 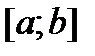 .
.
Геом. смысл определенного интеграла состоит в том, что 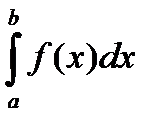 =S криволин. трапеции, ограниченной сверху графиком ф-и
=S криволин. трапеции, ограниченной сверху графиком ф-и 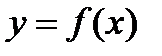 (f(x)≥0), снизу осью Ох, слева и справа- прямыми х=а и х=в.
(f(x)≥0), снизу осью Ох, слева и справа- прямыми х=а и х=в.
43. Св-ва опред. интеграла:
1) 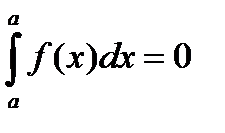
2)при перестановке пределов интегрирования, знак определенного интеграла меняется на противоположный

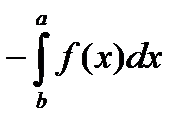
3)если  и
и  интегрируемы на
интегрируемы на 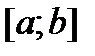 ф-и, тогда
ф-и, тогда  ±
± 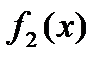 также интегрируемы. Причем
также интегрируемы. Причем
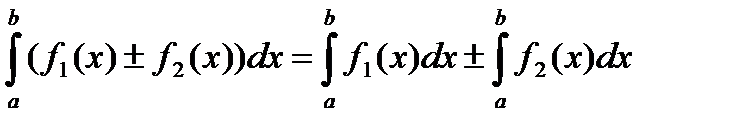
4)св-во аддитивности. Пусть 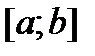 разбит на
разбит на 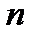 элементарных отрезков след. образом
элементарных отрезков след. образом 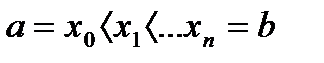 , тогда
, тогда 

5)постоянный множитель можно выносить за знак определенного интеграла.
6)если  интегрируема на
интегрируема на 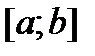 (a<b), причем f(x)≥0, тогда
(a<b), причем f(x)≥0, тогда 
7)пусть ф-и f(x) и g(x) интегрируемы на 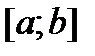 (a<b) и на всем отрезке f(x) ≤ g(x). Тогда
(a<b) и на всем отрезке f(x) ≤ g(x). Тогда 
8)пусть ф-я f(x) интегрируема на 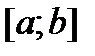 (a<b), тогда
(a<b), тогда 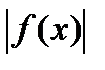 также интегрируема на
также интегрируема на 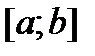 , причем
, причем 
Т. (об оценке опред. интеграла). Если ф-я  интегрируема на
интегрируема на 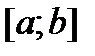 (a<b) и для всех
(a<b) и для всех  вып-тся нерав-во
вып-тся нерав-во  , тогда
, тогда
 Т. (о среднем значении) Если ф-я
Т. (о среднем значении) Если ф-я  непрерывна на
непрерывна на 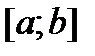 , то на этом отрезке существует точка с, такая что
, то на этом отрезке существует точка с, такая что 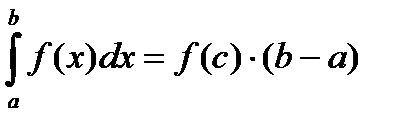
44. ф-ла Ньютона-Лейбница. Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то 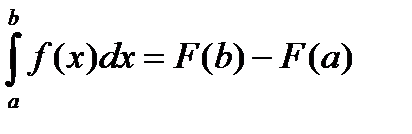
это выражение известно под названием формулы Ньютона – Лейбница.
Доказ-во: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция  - первообразная функция от f(x). Но т.к. функция может им.бесконечно много первообразных, кот. будут отличаться друг от друга только на какое – то постоянное число С, то
- первообразная функция от f(x). Но т.к. функция может им.бесконечно много первообразных, кот. будут отличаться друг от друга только на какое – то постоянное число С, то 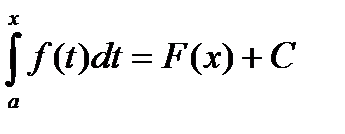
|
|
при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:
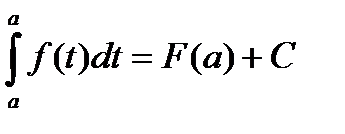


Тогда  .
.
А при х = b: 
Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
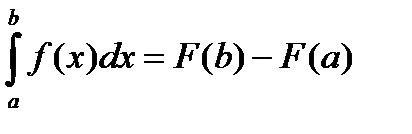
Теорема доказана.
Иногда применяют обозначение F(b) – F(a) = F(x)  .
.
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.
|
|
|

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!