Комбинаторное доказательство теоремы.

Приведенное ниже доказательство предоставлено В.К.Леонтьевым, его фрагменты можно найти в [6] и в [8].

Теорема.

Для любого R: 0 < R < C (ρ), такого что M=2^[nR], выполняется соотношение:

P *(M,n,p) 1.

Доказательство.

Пусть имеется код V_k L={ 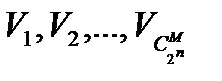}. Напомним, что P (V_k)– вероятность правильного декодирования для V_k.

Рассмотрим 3 функции:

 

Пусть A_k(i) – число векторов в Bⁿ, находящихся на расстоянии i от некоторого кодового слова кода V_k.

Тогда P (V_k) = - вероятность правильного декодирования V_k. Здесь . Действительно, каждое слагаемое в этой сумме равно единице, если выполняются все три условия:

1) ,

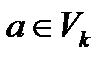2) расстояние от a до b равно i,

3) b декодируется в a.

В формуле для вероятности правильного декодирования P (V_k) параметр A_k(i) – это число точек из , которые находятся на расстоянии i от некоторого кодового слова и декодируются в это кодовое слово.

Всего таких кодов : , .

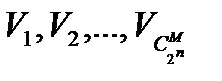Усредняем вероятность правильного декодирования по всем кодам и получаем среднюю вероятность правильного декодирования

=

Рассмотрим саму внутреннюю сумму в последней формуле приведенных выше выкладок. Эта сумма равна числу кодов V_k таких, что 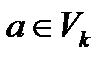, и b декодируется в a. Заметим, что точка b обязательно декодируется в a тогда и только тогда, когда в коде V_k нет кодовых точек расположенных к b ближе, чем точка a. Это означает, что в шаре (обозначим его S(a,b)) радиуса ρ(a,b) с центром в точке b нет других точек кода V_k. Поэтому, если точки a,b фиксированы, то остальные (M -1) точку кода мы можем выбирать произвольным образом из множества Γ= Bⁿ\ S(a,b). Мощность этого множества , где количество точек из в шаре радиуса ρ. (Так как это количество не зависит от x, а зависит только от nи ρ, то, чтобы подчеркнуть этот факт, ниже при необходимости мы наряду с обозначением будем пользоваться и другим - ). Отсюда следует, что упомянутая внутренняя сумма равна .

Отметим два комбинаторных факта и продолжим начатую выше цепочку соотношений.

1) Число пар точек из , лежащих на расстоянии iравно

2) Справедливо известное комбинаторное равенство

 

Далее имеем

(=) (#)

Мы доказали одно из основных равенств (помеченное(#)), которое будем использовать ниже.

Отметим несколько моментов:

1) Функция выпукла вверх.

2) Тогда функция выпукла вниз.

3) Сумма выпуклых функций выпукла.

4) Выпуклая функция от выпуклой функции выпукла.

5) Отсюда следует, что функцияf(i)= является функцией, выпуклой вниз.

6) Вспомним неравенство Йенсена. Пусть даны числа α ₁ …α_n,α_i> 0, . Тогда для выпуклой вниз функции f(x) справедливо неравенство.

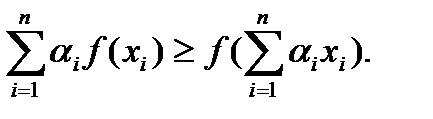
7) В качестве α _i возьмем 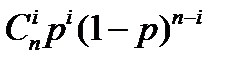. Очевидно, что 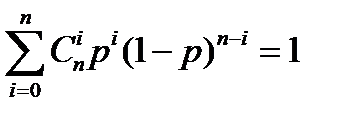, а .

Используя 1-7, получим

. (##)

Далее используем очевидные соотношения

. (###)

Заметим далее, что максимальная вероятность больше средней, т.е.

P *(M,n,p)≥ .

Из этого факта и соотношений (#), (##), (###) получаем:

P *(M,n,p)≥ = .

Далее

= =

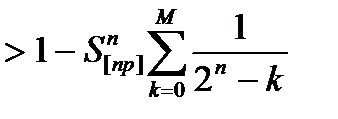Теперь устремляем n→∞ и раскладываем в ряд, оставляя главные члены каждого слагаемого. Получаем

= 1- ( =

=1- О(),

Что асимптотическипри n→∞ равно

Вспомним лемму (**)|

S_[pn] (x)| ≤ 2^{nH ( p )}.

Кроме того, заметим, что по условию: 0 < R < C (ρ), M=2^[nR].Отсюда получаем

≥ 2^{nH ( p )}≥ = 1- 2 ^n(R-C(p)).

Таким образом мы доказали, что при 0 < R < C (p) и n→∞ справедливо неравенство

P *(M,n,p)>1- 2 ^n(R-C(p)).

Но это значит, что P *(M,n,p)→1при n→∞.

Теорема доказана.

Вы можете сравнить эти два доказательства. Первое доказательство короче и кажется более простым. Однако это, на самом деле, не так. Для привлечения необходимого аппарата теории вероятностей схема декодирования содержит определенные сложности, которые мы оставили без комментариев. Подробный разбор этих сложностей будет достаточно громоздким и «затемнит» доказательство.

Хотя второе доказательство длиннее и выглядит технически более сложным, но оно идеологически более понятное и прозрачное, кроме того, оно «замкнуто» в себе и не требует апелляций к идеям теории вероятностей.

Теорема Шеннона – это теорема существования, и она не дает методов построения кодов. Разбор, классификация и общее представление совокупности таких методов – предмет отдельной дисциплины – Теории кодирования. Однако, мы взялись описать в общих чертах основную идеологию Теории информации, поэтому ниже, в двух последних разделах, будут приведены несколько примеров построения конкретных кодов.

А что будет, если R>C(p)? На этот вопрос отвечает третья Теорема Шеннона.

Теорема. (Третья теорема Шеннона.) Для любого R: R > C (p)>0, такого что M=2^[nR], не существует кода C, для которого бы выполнялось соотношение:

P_C (M,n,p)→1при n→∞.

Мы оставим эту теорему без доказательства. Доказательство этой теоремы базируется на нескольких фактах (см. [8]). В лемме (*) было доказано, что | B_pn (x)| ≤ 2 ^{nH ( p )}.На самом деле, справедлива более точная оценка: | B_pn (x)| ~ 2 ^nH(p) (при n → ∞). И это асимптотическое равенство достигается для совершенных кодов (см. ниже). В итоге получим, что k = n – nH (p) для совершенного кода. А отсюда можно получить, что максимум вероятности правильного декодирования достигается именно на совершенном коде. После этого в качестве кода C при доказательстве теоремы можно брать только совершенный код. А это уже конструкция с определенными свойствами, которые и используются для доказательства теоремы.

Замечание.

Интересно обратить внимание, что при доказательстве теоремы Шеннона мы использовали, например, вместо максимума вероятности правильного декодирования среднюю вероятность такого декодирования. И уже эта средняя стремилась к единице. А это наилучший случай. То сеть получается, что в некотором смысле, поиск наилучшего варианта не дает никаких существенных преимуществ по сравнению со средним случаем. С практической точки зрения, это может показаться странным.

 

Примеры кодов, исправляющих ошибки. Линейные коды.

Класс (n,M,d)-кодов очень широкий, поэтому естественным является стремление его проанализировать, выделить в нем специальные множества кодов. Такое выделение происходит за счет задания дополнительных свойств. В дальнейшем использование этих свойств помогает при построении кода.

Линейные коды.

Наложим на множество C ограничение, превратим его из подмножества в подпространство Bⁿ.

Это даст возможность использовать результаты линейной алгебры.

Опр.: Код C Bⁿ называется линейным (групповым), если для любых α, β C: α + β C.

Сразу из определения следует, что групповому коду обязательно принадлежит нулевой вектор.

Заметим, что если код не является бинарным, то понятия линейного и групповых кодов не совпадают.

В случае бинарного кода: Bⁿ – линейное пространство; зададим в нем подмножество векторов C Bⁿ, и для любых α, β C: α + β C. Отсюда следует, что вместе с любым набором вектров линейному коду принадлежит их линейная комбинация, поэтому C – подпространство Bⁿ.

Пусть dimC = k, | C | = 2 ^k. Согласно определению: если C – групповой код.

Легко показать, что d (c) = min | α | (α С, α 0).

Для любого линейного кода существуют 2 матрицы: G – порождающая, H – проверочная.

Порождающая матрица состоит из векторов (записанных в строке покомпонентно) некоторого базиса подпространства C. Для любого β C: β – линейная комбинация строк G. Если dimC = k, то G должна содержать k строк.

Проверочная матрица кода C – это такая матрица, что для любого α С:

αH^T = 0.

При построении кода (алгоритмов кодирования и декодирования) C чаще используется матрица H.

Опр.: Код С* Bⁿ называется ортогональным C, если для любых α, β: α С*, β С выполняется условие: αβ = 0.

Из курса линейной алгебры известно, что если dimC = k, то dimC* = n – k. При этом порождающей матрицей H* кода С* является проверочная матрица H кода С. (И наоборот.)

Пример: Код с проверкой на четность.

dimC = n – 1, dimH = 1, H = (11…1)_{1x n}

Рассмотрим теперь операции преобразования кодовых матриц.

Элементарные преобразования матриц:

1) Перемена местами строк.

2) Умножение строки на число.

3) Сложение строки с линейной комбинацией других строк.

4) Перемена столбцов местами.

Опр.: Коды C и D называются эквивалентными, если G (C) можно получить из G (D) с помощью элементарных преобразований.

Утверждение: Для любого С существует эквивалентный код С’ такой, что

Опр.: Код с порождающей матрицей вида () называется систематическим.

В таком коде в подматрице 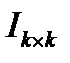находятся информационные столбцы, в - проверочные столбцы. (См. Раздел 10.2.2).

Проверочных символов (n – k). В H (C’) (n – k) строк, каждая строка – соотношение, задающее линейную комбинацию: 1-я – 10…0, 2-я – 01…0 и т.д.

Пример.

n = 5, k = 3 и

Пусть α ₁, α ₂, α ₃ – информационные символы, α ₄, α ₅ – проверочные. Тогда проверочные соотношения:

Алгоритм кодирования осуществляется следующим образом: любая строка H дает проверочную комбинацию. Так мы преобразуем слова из B^k, подлежащие передаче, просто добавляя к ним n-k символов–результаты проверочных соотношений после подстановки туда информационных символов.

Заметим, что в нашем примере мы получили код с d (C) = 2.

В общем случае для декодирования с помощью таблицы декодирования на декодере хранится и в процессе алгоритма декодирования обрабатывается таблица, содержащая n2ⁿсимволов (2ⁿ векторов). В начале курса мы уже видели, насколько сложно работать с экспоненциальным объемом информации.

Свойство линейности кода позволяет в этом вопросе получить существенную выгоду. Для хранения таблица декодирования нужно хранить ее первую строку и первый столбец, т.е. 2^n-k+2^k векторов. Это следует из того, что линейный код B^k – это подгруппаабелевой группыBⁿ.

Раскладывая группу по подгруппе мы получаем таблицу декодирования в виде матрицы, первая строка которой, как обычно, векторы кода, а остальные – смежные класс. Тогда первый столбец – это образующие смежных классов.

Для линейных кодов такой алгоритм декодирования называется декодированием с помощью «стандартной расстановки».

Опр.: Синдром линейного кода называется вектор S_α = αH^T.

Если проверочная матрица имеет (n— k)строк, то синдром S_yпроизвольного вектора у из Bⁿявляется вектором длины (n— k).

Поскольку по определению линейного кода вектор у является кодовым тогда и только тогда, когда yH^T = 0, то справедливо следующее утверждение.

Утв. Синдром S_y вектора у равен 0 тогда и только тогда, когда у является кодовым вектором.

Утв. Для двоичного линейного кода синдром S_y принятого вектора у равен сумме тех столбцов проверочной матрицы H, где произошли ошибки.

Утв. Пусть U – кодовое слово,при передаче из него получено словоV= U+e,где вектор e – вектор ошибки. Алгоритм на основе стандартной расстановки правильно декодирует слово тогда и только тогда, когда вектор ошибки – образующая смежного класса.

Оно вытекает из следующего утверждения.

Утв. Два вектора u и v принадлежат одному и тому же смеж­ному классу тогда и только тогда, когда их синдромы равны.

Достаточно важным для линейных кодов является следующее простое утверждение.

Теорема. Кодовое расстояние линейного кода d (C) = d, тогда и только тогда, когда любые (d – 1) столбцов H линейно-независимы и данное d является максимально возможным.

Спектр кода.

Существует еще одна важная характеристика кода – это спектр кода.

Рассмотрим код V = (v ₁… v_k). Пусть для кодового слова v_i величина r_s (v_i) – это число кодовых слов таких, что ρ (v_j, v_i) = s. Тогда вектору v_i сопоставляется (r ₀(v_i)… r_k (v_i)) – спектр v_i – кода. А спектры всех кодовых точек можно задавать в виде таблицы размером (k+1)xk.

Если V – линейный код, то спектры всех v_i одинаковые. Поэтому для линейного кода спектром называется вектор (a ₀… a_n), т.е. число кодовых слов весов 0… n.

Важным инструментом использования спектра является теорема Маквильямс.

Теорема ( Маквильямс).

Пусть есть код V и его спектр (a ₀… a_n) и код ортогональный V * и его спектр (b ₀… b_n), тогда справедливо соотношение , где z –переменная.

Эта теорема дает возможность выражать спектр кода через спектр ортогонального кода.

Оно имеет несколько важных следствий, применяющихся не только в теории кодирования, но в комбинаторике. Приведем некоторые из них.

Следствие1. Пусть . Тогда справедливо соотношение

.

Доказательство. Так как , то из

с использованием теоремы Маквильмс получаем

.

Приравнивая коэффициенты при одинаковых степенях, имеем

.

Следствие доказано.

Заметим, что из следует, что

.

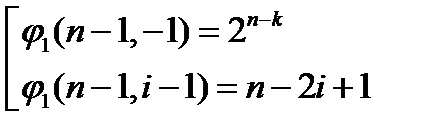Следствие 2. Справедливо соотношение

, где - число точек B_n веса sна расстоянии r от некоторой точки кода.

Пусть C (s) – число точек Bⁿ веса s, попавших в шар радиусаt линейного кода, исправляющего t ошибок.

Следствие 3. Справедливо соотношение:

.

Ниже мы приведем пример использования этих соотношений.

 

Код Хэмминга.

Код Хэмминга в то же время является уникальным по структуре объектом, обладающим несколькими интересными свойствами. Это линейный код, это совершенный код, Код, дуальный к коду Хэмминга, является эквидистантным кодом.

Описать код – это описать множество Cиз 2 ⁿ. Код Хэмминга принято задавать через его проверочную матрицу.

Пусть m – натуральное число. Проверочная матрица кода имеет размеры mx (2^m-1).

В столбцах находятся все ненулевые последовательности длины m, представляющие собой двоичную запись числа – номера столбца. Очевидно, что любые два столбца линейно независимы, а среди троек столбцов уже есть линейно зависимые наборы.

Поэтому, согласно приведенной выше теореме, кодовое расстояние кода Хемминга d =3. Следовательно, этот код исправляет ровно одну ошибку.

Сразу из определения проверочной матрицы кода Хэмминга следует простой алгоритм декодирования. Декодирование происходит сразу после вычисления синдрома принятого слова y. Для принятого слова yесть три возможности:

1. Ошибок не было. Тогда синдром S = y H^T=0.

2. Ошибка ровно одна. Тогда синдром является двоичной записью (индикатором) номера бита, в котором произошла ошибка, так как для линейного кода сидром – сумма столбцов проверочной матрицы, в которых произошли ошибки. В нашем случае ошибка одна, а столбец – номера столбца

3. Произошло более одной ошибки. Тогда код Хэмминга не обеспечивает защиты от ошибок.

Пример.

m = 3, n = 2³ – 1 = 7, k = 4. Пусть информационными будут символы ().

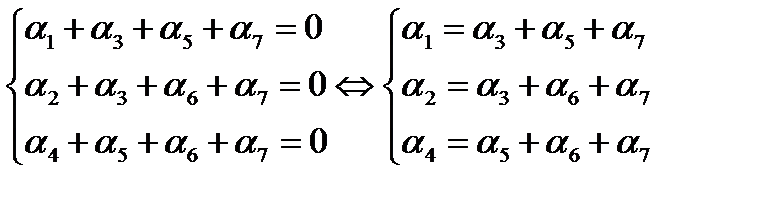
U = 1100 → 0 1 1 1 1 0 0

Если U – передано, U ’ – получено, рассмотрим 3 случая:

Заметим, что в данном примере .

Рассмотрим теперь свойства кода.

Длина кодовых слов n = 2 ^m – 1. Число проверочных символов m = log (n + 1). Число информационных символов равно 2 ^m – 1 - m. Отсюда следует, что число кодовых слов | C | в коде Хэмминга | C | = 2 ⁿ / (1 + n).

Заметим теперь, что число точек в шаре радиуса единица равно 1 + n, и вспомним приведенную выше границу Хэмминга:

.

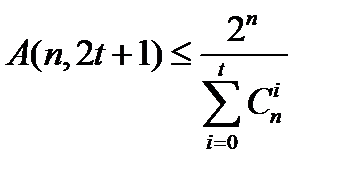Код Хемминга исправляет одну ошибку и A (n, 3) = 2 / (1 + n). Получаем, что для Хемминга граница Хемминга достигается, шары вокруг кодовых точек покрывают все пространство Bⁿ.

Опр.: Код С, исправляющий t ошибок, называется совершенным, если . Совершенный код – код, на котором достигается граница Хемминга.

Таким образом, мы доказали утверждение.

Утв. Код Хэмминга является совершенным кодом.

Применим теперь теорему Маквильямс.

Так как код Хэмминга - совершенный код, то число кодовых точек веса s, попавших хотя бы в один шар радиуса единица с центром в кодовой точке, равно общему числу точек веса s, т.е. C (s) = C^S_n.

Применяя Следствие 3 из теоремы Маквильямс, получаем

.

Но φ₁(n-1,-1)=2^n-k. Тогда

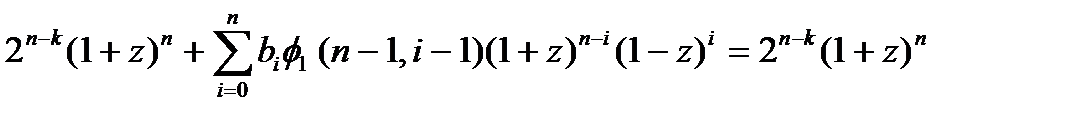, т.е.

.

Т.к. многочлен равен нулю, то все его коэффициенты равны нулю:

Но Отсюда следует, что только при i=(n+1)/2, т.е.

 

b ₁ = b ₂ = … = b _{(n – 1) / 2} = b _{(n + 3) / 2} = … = b_n = 0

n – 2 i + 1 = 0

i = (n + 1) / 2

Т.е. b _{( n – 1) / 2} не равно 0, а значит спектр кода V * равен(0, 0…0, (n + 1) / 2, 0…0). Заметим, (n+1)/2=2^m-1.

Получаем интересный код, который принадлежит к определенному классу кодов.

Опр.: Код называется эквидститантным, если для любых i, j (i ≠ j): ρ (v_j, v_i) = d.

Таким образом, мы доказали следующее утверждение.

Утв. Код, двойственный коду Хемминга является эквидистантным кодом/

Этот код называется кодом Макдональда.

Параметры кода Макдональда: n = 2 ^m – 1, k = m, d=(n+1)/2.

Тогда все ρ (…) = 2 ^{m – 1} (число точек в коде Макдональда 2 ^m)

Применим теорему Плоткина: A (n, d) ≤ 2 d / (2 d – n)для кода Макдональда и получим:

2 d / (2 d – n) = 2*2 ^{m -1} / 2*2 ^{m -1} – (2 ^m – 1) = 2 ^m

Отсюда следует, что любой эквидистантный код не может содержать более чем 2 ^m точек. Поэтому код Макдональда оптимален, лучше ничего не построить.

Оказывается «мощностное свойство» кода Макдональда справедливо для любых эквидистантных кодов.

Теорема: Пусть V – эквидистантный линейный код в Bⁿ, тогда | V | ≤ n + 1.

Доказательство. Пусть V = (V ¹,…,V ^s), и при этом ρ (V _j, V _i) = d, если i ≠ j.

Тогда имеем

Будем считать, что 0 V и пусть это будет первый вектор кода, т.е.

.

Определитель Грамма для векторов :

- линейно независимы.

Итак, имеем S- 1 линейно независимых векторов.

В пространстве Bⁿ может быть не более n линейно независимых векторов

S n +1.

Теорема доказана.

Грубо говоря, требование симметрии типа эквидистантности приводит к тому, что в коде остается всего порядка log(| Bⁿ |) точек.

БЧХ – коды

В начале 1950-х годов в теории кодирования была поставлена задача построить возможное обобщение кода Хэмминга - код, исправляющий t ошибок. Для этого потребовалось порядка 10 лет.

Стояла задача построить (n,k)- код с минимальным числом строк проверочной матрицы и заданным кодовым расстоянием d. Обозначим это минимальное число строк такого кода через m(n,d).

В основу легли идеи:

1. Построить такую проверочную матрицу, у которой кодовое расстояние 2 t + 1 (2 t столбцов линейно-независимы).

2. Используя алгебраические свойства кода, построить алгоритм кодирования (декодирования).

3. Определитель Вандермонда

для матрицы, состоящей из различных элементов поля (α_i≠α_j; i,j=1,…,n) не равен нулю, поэтому любые d-1 столбцов этой матрицы линейно независимы.

4. Рассмотрим построение проверочной матрицы. Пусть l₁, l₂, …, l_t - локаторы ошибок – двоичные записи номеров битов, в которых произошли ошибки. Тогда проверочная матрица строится так, что ее строки задают проверочные отношения по следующей схеме:

 

Получаем t уравнений с t неизвестными, при декодировании решаем их и находим, где произошли ошибки.

Опишем на следующем примере основную идею декодирования.

Пример. Рассмотрим БЧХ-код, исправляющий две ошибки.

Его проверочная матрица состоит из двух половин: первая половина (верхняя часть матрицы) – та же, что и у кода Хэмминга. Предположим, что множество вектор - столбцов верхней половины – элементы поля. (Т.е. их можно складывать, вычитать, умножать и делить.) Тогда вторая половина проверочной матрицы – значения некоторой функции f(i) от векторовпервой половин, например, столбцы первой, возведенные в куб (нельзя брать квадраты, потому что квадрат суммы в некоторых полях равен сумме квадратов).

В этом случае первая половина γ вектора синдрома задает, как и раньше, сумму позиций i и j, в которых произошла ошибка, а вторая половина - δ – сумму кубов этих позиций. Если произошло две ошибки, то мы получаем два уравнения с двумя неизвестными. Решаем их (а в поле это можно сделать!) и находим позиции ошибок.

Сказанное проиллюстрировано ниже.

Мы имеем систему двух уравнений с двумя неизвестными:

В поле GF(2ⁿ) (см. Замечание ниже) можно получить:

.

Отсюда

.

Тогда удовлетворяют уравнению .

Это уравнение решается в поле GF(2ⁿ) и всегда имеет там два корня.

Замечание.

На практике вектора i иj называются векторами локаторов ошибок (или просто локаторами ошибок), а многочлен, корнями которого являются вектора, мультипликативно обратные локаторам ошибок, называется многочленом локаторов ошибок. И именно он используется в алгоритмах кодирования и декодирования, вместо приведенного выше.

В общем случае это следующий многочлен:

,

где произведение берется по всем локаторам ошибок.

Для нашего примера о н выглядит так: .

Пусть α ₁… α_n – элементы поля GF (2 ^k), а γ ₁,γ ₂,…, γ _i - соответствующие им двоичные векторы, записанные в виде столбцов.

Рассмотрим матрицу.

- (0,1)-матрица размера knxn.

Теорема: Любые 2 S столбцов матрицыMлинейно-независимы.

Доказательство. От противного. (Всюду «+» означает сложение по модулю 2).

Заметим, что (α ₁ + … + α_n)² = α ₁² + … + α_n ² (1)

Пусть существует h столбцов (h ≤ 2 S), являющихся линейно-зависимыми. Это столбцы с номерами i ₁… i_h, тогда

γ ^{2 t -1} _{i 1} + … + γ ^{2 t -1} _ih = (0…0) ^T, t = 1… S

Если перейти к элементам поля получим:

α ^{2 t -1} _{i 1} + … + α ^{2 t -1} _ih = 0, t = 1… S (2)

Для любого четного q (1 ≤ q ≤ 2 S): можно представить q = 2 ^U (2 t – 1), U ≥ 1, t ≤ S

Применим соотношение (1) к равенству (2) U раз и получим:

α ^q _{i 1} + … + α^q_in = 0. (3)

Таким образом

α ^j _{i 1} + … + α ^j _in = 0приj=1,…,2S.

Возьмем матрицу M,определитель любого минора порядка (d – 1) будет представлять собой определитель Вандермонда порядка d – 1. А он не равен нулю.

Теперь возьмем d = 2 S + 1, т.о. любой минор порядка 2 S не равен 0. Отсюда следует, что любые 2 S столбцов линейно-независимы.

Получили противоречие с соотношением(3).

Теорема доказана.

Следстви. Матрица может быть проверочной матрицей (n, k) – кода, исправляющего S ошибок.

Примеры.

Код Хэмминга является БЧХ-кодом с кодовым расстояние 3 и исправляет одну ошибку.

Проверочная матрица кода с расстоянием 5 строится из двух частей. Верхняя часть – проверочная матрица кода Хэмминга. Нижняя половина – столбцы верхней половины, возведенные в куб (эти столбцы трактуются как элементы описанного выше поля. Схема декодирования приведена выше.

Для случая трех ошибок проверочная матрица состоит уже из трех частей. Третья часть – это столбцы первой части, возведенные в пятую степень. Многочлен денумераторов ошибок имеет третью степень. Пусть произошло 3 ошибки в позициях η, δ, ζ. Тогда при рассмотрении верхней части матрицы η + δ + ζ = ρ ^*; второй части: η ³ + δ ³ + ζ ³ = ρ ^**; третьей части: η ⁵ + δ ⁵ + ζ ⁵ = ρ ^***. Получаем систему из трех уравнений с тремя неизвестными.

Теория и алгоритмы решения уравнений в конечных полях хорошо разработаны, поэтому решение уравнений в алгоритме декодирования БЧХ-кода не представляет труда. Конечно, чем больше S, тем больше сложность алгоритма.

Число проверочных символов БЧХ-кода для исправления S ошибок (упомянутое выше минимальное число строк проверочной матрицы) подчиняется соотношению:

m(n,d) ~ slogn

k = n – slogn при n → ∞, k → n.

Утверждение. Для любой бесконечной последовательности (n,k,d)-кодов БЧХ над GF(q) скорость кода k/n и отношение d/n стремятся к нулю с ростом n.

Замечание.

Опр. Линейный код длины п называется циклическим, если для любого кодового слова (x₁,x₂,..., x_n) слово (x₂,...,x_n,x₁)также является кодовым.

БЧХ-код является циклическим кодом.

Циклические коды обладают несложными процедурами кодирования и декодиро­вания, имеют хорошие алгебраические свойства, их группы автоморфизмов содержат циклические подстановки. Все совершенные линейные коды, коды Рида-Маллера и другие коды являются кодами, которые после пе­рестановки координат и несущественной модификации оказываются циклическими. Многие важнейшие блоковые коды, открытые позже, также оказались либо циклическими, либо тесно связанными с ними.

Построение БЧХ-кодом явилось качественным прорывом не только в такой математической дисциплине как теория кодирования, но и в инженерных технологиях защиты информации от шума в канале.

Выше мы уже упоминали о том, что в протоколах передачи информации встают вопросы синхронизации скорости генерации кодовых слов, скорости передачи и пропускной способности канала.

Таким же важным вопросам для адаптивных протоколов является подбор соответствия корректирующей способности кода и качества канала. Очевидно, что при вероятности ошибки в канале p=0,2 и длине кодового слова n=10 использование кода с d=4 или даже 5 означает сознательное согласие на то, что информация будет частично искажаться. Если же кодовое расстояние будет, например, 20, то вероятность искажения информации будет меньше, чем 10^-10.

Отсюда следует, что при построении протокола передачи необходимо учитывать такие свойства информации, как важность, ценность, чувствительность к искажению. Для их учета нужно уметь их измерять (кодировать в широком смысле!). Но для этого нужно дать им определение.

Как ни странно, на сегодня этот вопрос еще малоизучен. В протоколах передачи в лучшем случае используются эвристики и экспертные оценки. Типичный подход: «Данная информация является важной и требует передачи с гарантией безошибочности P_γ=10^-9.»

А если мы хотим передавать по каналу разные типы информации? На практике для этого используются не только разные каналы, но и разные сети. В то же время, с математической точки зрения, очевидно, что, зная p, n и P_γ, можно подобрать d.

Такого сорта протоколы нельзя построить, имея в своем распоряжении только код, исправляющий одну ошибку. Именно появление кодов с различными значениями параметра d (например, БЧХ-кодов) дало такую возможность.

Заключение.

Предложенный здесь текст обладает рядом свойств.

1. Он является базовым как для объема 17 лекций – 17 семинаров, так и для объема 34 лекции – 17 семинаров.

2. Сам материал является классическим и в той или иной мере присутствует в аналогичных курсах ведущих Вузов России. Однако, подбор материала, логика изложения и акценты являются во многом нетрадиционными и ориентированы на специфику подготовки студентов кафедры ИУ-8.

3. Для студентов, желающих углубить и расширить свои знания в этой области, автор постарался привести (в минимальном объеме) необходимые источники, освоение которых должно быть не очень затруднительным при условии овладения предлагаемым здесь текстом лекций..

4. Предполагается, исходя из методического плана подготовки на кафедре ИУ-8, что студент, освоивший предмет в полной мере, готов к пониманию достаточно глубокого курса теории кодирования (если, конечно, он освоил и алгебру).

5. Во многом тематика данного курса явилась поводом для изложения в нем подготовительных материалов для другой дисциплины- курса по выбору: «Дополнительные главы дискретного анализа».

Вопросы для самопроверки.

Ниже предлагается название минимального количества тем (вопросов), которые с