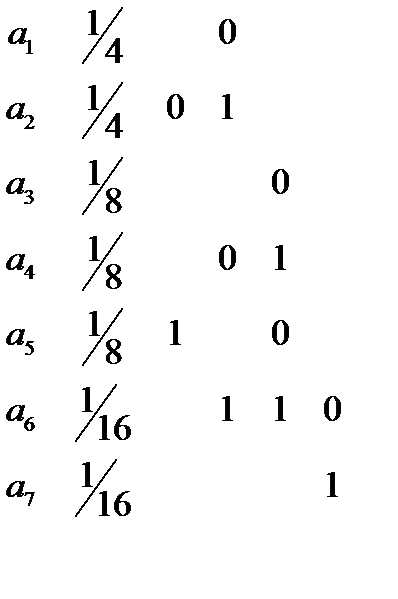Заметим, что Энтропия по Хартли является частным случаем энтропии по Шеннону. Если все  , то H (A) = log n, а это и есть Энтропия по Хартли множества из n элементов.В общем случае справедливо следующее утверждение, которое показывает, что энтропия по Хартли является оценкой сверху для энтропии по Шеннону. То есть ситуация равновероятных событий наихудшая с точки зрения информативности.
, то H (A) = log n, а это и есть Энтропия по Хартли множества из n элементов.В общем случае справедливо следующее утверждение, которое показывает, что энтропия по Хартли является оценкой сверху для энтропии по Шеннону. То есть ситуация равновероятных событий наихудшая с точки зрения информативности.
В следующем и других доказательствах нам потребуется математический факт, известный как неравенство Йенсена.
Неравенство Йенсена. Пусть даны числа α 1 …αn,αi> 0,  . Тогда для выпуклой вверх функции f(x) справедливо неравенство.
. Тогда для выпуклой вверх функции f(x) справедливо неравенство.


Для выпуклой вниз функции выполняется противоположное неравенство:

Теорема: Пусть имеется случайный источник, который генерирует буквы алфавита A = (a 1 …an) с вероятностями p 1 …pn, тогда справедливо соотношение
H (A) =  .
.
Доказательство. Рассмотрим функцию f (x) = -x log x. Так как f’ (x) = - log x – 1 /ln 2 и f’’ (x) = - 1 /x, то при x ≥ 0 функция f (x) выпукла вверх. Тогда для нее справедливо неравенство Йенсена: 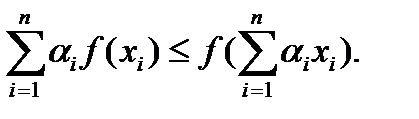 Возьмем α 1 …αn,αi> 0,
Возьмем α 1 …αn,αi> 0, 
Положимα i = 1 /n, xi = pi,i=1,…,n.
H (A) = 
Здесь мы учли, что 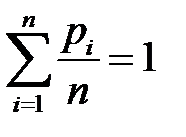 /n.
/n.
Теорема доказана.
Теорема Шеннона
Рассмотрим теперь математическую модель, являющуюся объединением двух предыдущих. Случайный источник генерирует буквы алфавита А = (а 1, …, аn), к которым потом применяется некоторый алгоритм алфавитного кодированияφ. (Каждой букве ai алфавита A ставится в соответствие Bi=φ(ai) – словодлины li в алфавите B = (b 1, …, bq)). Как можно оценить качество такого алгоритма?
В случае вероятностного источника такие количественные характеристики алгоритма как  или
или  уже не являются информативными, так как не зависят от вероятностей.
уже не являются информативными, так как не зависят от вероятностей.
В этом случае удобно использовать величину  , которая характеризует среднее количество букв алфавитаB, приходящееся на один символ алфавита Aпри алфавитном кодировании φ. (Назовем эту величину стоимостью кодированияφ). Пусть теперь
, которая характеризует среднее количество букв алфавитаB, приходящееся на один символ алфавита Aпри алфавитном кодировании φ. (Назовем эту величину стоимостью кодированияφ). Пусть теперь  , где минимум берется по всем возможным дешифруемым алгоритмам алфавитного кодирования (при заданных алфавитахA иB и распределении вероятностей p 1 …pn). (Назовем эту величину минимальной стоимостью кодирования).
, где минимум берется по всем возможным дешифруемым алгоритмам алфавитного кодирования (при заданных алфавитахA иB и распределении вероятностей p 1 …pn). (Назовем эту величину минимальной стоимостью кодирования).
Если бы мы знали C(A), то смогли бы оценить качество нашего алгоритмаφ.
Следующая теорема (она известна под названием теоремы Шеннона для канала без шума) дает ответ на этот практически важный вопрос.
Теорема. Справедливо соотношение
 .
.
Доказательство.
1) Сначала докажем оценку снизу:
 .
.
В следующих выкладках все суммы берутся по i=1,..,n. Используется известное из математического анализа неравенство l nx  x– 1, log x
x– 1, log x  (x– 1)log e, а также неравенство Крафта (суммирование везде ведется от 1 до n).
(x– 1)log e, а также неравенство Крафта (суммирование везде ведется от 1 до n).

 (
( – по неравенству Крафта,
– по неравенству Крафта, 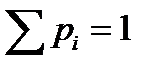 ).
).
2) Для доказательства оценки сверху мы построим конкретный алгоритм алфавитного кодирования ϕ(известный как алгоритм Шеннона-Фано). Ведь если оценка сверху будет выполняться для некоторого Cϕ(A), то она будет выполняться и для C(A).
В данном коде набор длин задается следующим соотношением.
 (целая часть с избытком (сверху)).
(целая часть с избытком (сверху)).
Проверим, удовлетворяет ли этот набор неравенству Крафта.
 ,
, 
 неравенство выполняется.
неравенство выполняется.
Теперь построим код точно также, как это делалось выше при доказательстве теоремы о существовании префиксного кодав случае выполнения неравенства Крафта (мы строили сначала слова Bi длины 1, затем слова длины два и т.д.).
Оценим теперь сверху величину Cϕ(A) для этого кода.
Cϕ(A) =  .
.
Теорема доказана.
В наших примерах часто будет использоваться двоичный алфавит. Очевидно, что для случая бинарного алфавита В получаем неравенство
Н (А)  С (А)
С (А)  Н (А) + 1.
Н (А) + 1.
Алгоритмы кодирования
Алгоритм Шеннона (Фано).
Передаваемые символы располагаются в порядке убывания (или возрастания) вероятностей. Построим таблицу, первым столбцом которой являются идентификаторы передаваемых символов. Назовем, например, верхней частью этой получившейся последовательности символов ту, которая начинается минимального номера. Эта упорядоченная последовательность фиксируется, затем идут шаги алгоритма.
Каждый шаг – это горизонтальное деление пополам этой последовательности, а i-й шаг – деление одной из выбранных на предыдущем этапе частей.
Рассмотрим частный случай бинарного алфавита. В этой ситуации деление происходит на две части, а в общем случае – на qчастей.
Деление происходит так, чтобы в каждой половине суммы вероятностей отличались бы на минимально возможную величину (при нескольких вариантах берется, например, с избытком часть с наименьшими номерами букв).
Затем каждое деление порождает символ алфавита B, который приписывается при каждом делении к коду верхней части добавляется 0, а нижней – 1.
Так происходит до тех пор, пока в каждой из получившихся частей не останется по одному элементу. Тогда приписанные части последовательности нулей и единиц и будут кодами этих элементов.
Пример.
Нужно передавать семь букв. Их вероятности заданы. Схема алгоритма приведена ниже.
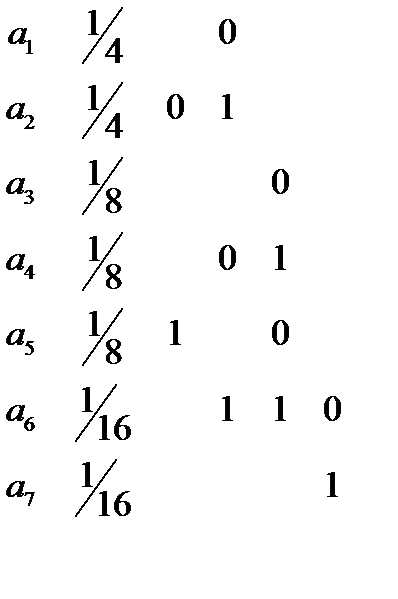
Такимобразом:
a 1 00
a 2 01
a 3 100
a 4 101
a 5 110
a 6 1110
a 7 1111
Стоимость кодирования 2,625. Энтропия:
H = 1/4 log 4 + 1/4 log 4 + 1/8 log 8 + 1/8 log 8 + 1/8 log 8 + 2 * 1/16 log 16 = 2, 25
Пример.

Стоимость кодирования 2,28.
H = 7/18 log 18/7 + 1/2 log 6 + 1/5 log 9 = 2,17
Алгоритм Хаффмана
Алгоритм дает результат не хуже, чем метод Шеннон-Фано. Более того, можно показать, что стоимость кодирования этим алгоритмом равна C(A).
Для случая двоичного кодирования код строится при помощи бинарного корневного дерева. (В случае произвольного qиспользуется q-арное дерево). Из каждой вершины выходит два ребра: правое помечаем 1, левое – 0. Листья такого дерева кодируются последовательностью пометок от корня к листу. Очевидно, что множество соответствующих этим листьям слов образует префиксный код.
Вначале мы строим вершины дерева (листья), соответствующие передаваемым буквам. Они помечаются значениями вероятностей. Затем на каждом шаге берутся две вершины с наименьшими пометками. Они образуют родительский узел, пометка которого равна сумме пометок вершин, и исключаются из дальнейшего рассмотрения. Шаги продолжаются до появления корня.
Пример.
Рассмотрим тот же пример, что и для кода Шеннона-Фано.
a 1 1/4
a 2 1/4
a 3 1/8
a 4 1/8
a 5 1/8
a 6 1/16
a 7 1/16
Итерации о построение листьев бинарного дерева.
(1, 2, 3, 4, 5, 6, 7) → (1, 2, 3, 4, 5, (6, 7)) → (1, 2, (3, 4), 5, (6, 7)) → (1, 2, (3, 4), (5, 6, 7)) → ((1, 2), (3, 4), (5, 6, 7)) → ((1, 2), (3, 4, 5, 6, 7))
Теперь, начиная с корня, строим пометки ребер дерева:
Получаем код.
и код:
1 00
2 01
3 100
4 101
5 110
6 1110
7 1111
Стоимость кодирования 2,625.



 , то H (A) = log n, а это и есть Энтропия по Хартли множества из n элементов.В общем случае справедливо следующее утверждение, которое показывает, что энтропия по Хартли является оценкой сверху для энтропии по Шеннону. То есть ситуация равновероятных событий наихудшая с точки зрения информативности.
, то H (A) = log n, а это и есть Энтропия по Хартли множества из n элементов.В общем случае справедливо следующее утверждение, которое показывает, что энтропия по Хартли является оценкой сверху для энтропии по Шеннону. То есть ситуация равновероятных событий наихудшая с точки зрения информативности. . Тогда для выпуклой вверх функции f(x) справедливо неравенство.
. Тогда для выпуклой вверх функции f(x) справедливо неравенство.


 .
.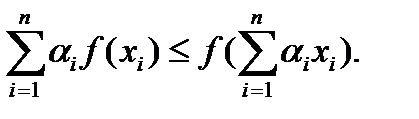 Возьмем α 1 …αn,αi> 0,
Возьмем α 1 …αn,αi> 0, 
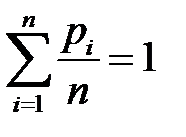 /n.
/n. или
или  уже не являются информативными, так как не зависят от вероятностей.
уже не являются информативными, так как не зависят от вероятностей. , которая характеризует среднее количество букв алфавитаB, приходящееся на один символ алфавита Aпри алфавитном кодировании φ. (Назовем эту величину стоимостью кодированияφ). Пусть теперь
, которая характеризует среднее количество букв алфавитаB, приходящееся на один символ алфавита Aпри алфавитном кодировании φ. (Назовем эту величину стоимостью кодированияφ). Пусть теперь  , где минимум берется по всем возможным дешифруемым алгоритмам алфавитного кодирования (при заданных алфавитахA иB и распределении вероятностей p 1 …pn). (Назовем эту величину минимальной стоимостью кодирования).
, где минимум берется по всем возможным дешифруемым алгоритмам алфавитного кодирования (при заданных алфавитахA иB и распределении вероятностей p 1 …pn). (Назовем эту величину минимальной стоимостью кодирования). .
. .
. x– 1, log x
x– 1, log x 
 (
( – по неравенству Крафта,
– по неравенству Крафта, 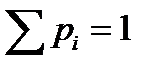 ).
). (целая часть с избытком (сверху)).
(целая часть с избытком (сверху)).
 неравенство выполняется.
неравенство выполняется. .
.