Пусть  - вектор ошибок. Он подчиняется распределению Бернулли, поэтому матожидание и дисперсия такого вектора
- вектор ошибок. Он подчиняется распределению Бернулли, поэтому матожидание и дисперсия такого вектора  и D(ξ)=np(1-p).
и D(ξ)=np(1-p).
Рассмотрим некоторый код C = { x 1… xM }, где { x 1… xM }– кодовые слова (вектора Bn).
Применяем декодирование в ближайшее слово (по принципу наибольшего правдоподобия и согласно приведенной выше схеме декодирования, а,в случае нескольких вариантов, в кодовое слово с наименьшим номером).Обозначим через T(C) таблицу декодирования.
ПередачаПрием
a x 1 T(C) – таблица
 b x 2
b x 2
… …
… xM

Зададим некоторое ρ>0. Тогда в ситуации 1 таблица Tρ(C) состаляется так, чтобы под каждым кодовым словом  в столбце находились все слова из Sρ (x i), а в ситуации 2 работают эвристические правила, примеры которых приведен выше.
в столбце находились все слова из Sρ (x i), а в ситуации 2 работают эвристические правила, примеры которых приведен выше.
Замечание.
Подчеркнем еще раз, что кодом называется любое подмножество булева куба Bn мощностью M. Поэтому не любой код будет кодом, исправляющим ошибки. Но к любому коду можно формально применить описанную выше схему декодирования. Все точки кода окружаем шарами радиуса ρ, а полученный вектор декодируем в центр шара. Если же вектор попадает в несколько кодовых шаров, то, возможно, что произошла ошибка декодирования. Правило, по которому в этом случае декодер производит декодирование несущественно. Например, применяется какое-нибудь дополнительное правило декодирования: в случайный, в ближайший и т.п.
Лемма ( ). Возьмем точку в Bn и шар S[pn] (x), оценим число точек в нем. Справедливо неравенство
). Возьмем точку в Bn и шар S[pn] (x), оценим число точек в нем. Справедливо неравенство
| S[pn] (x)| ≤ 2nH ( p )
Доказательство. | S[pn] (x)| =  .
.
Вспомним, что 0 ≤ p< 1\2,. Согласно принципу наибольшего правдоподобия – декодирование в ближайшее кодовое слово – выполняется соотношение
(1 – p)n≥ p(1 – p)n-1 ≥ … ≥pk(1-p)n-k.
Отсюда следует.

 ,
,
где 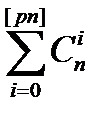 - мощность шара радиуса [pn].
- мощность шара радиуса [pn].
Тогда | S [ pn ](x)| ≤ (p [ pn ] (1 – p) n – [ pn ])-1 = 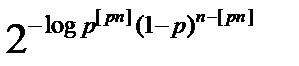 ≤ 2 nH ( p ).
≤ 2 nH ( p ).
Лемма доказана.
Пусть в канал передается вектор xi, а в декодер поступил векторY.
xi → канал → Y
Считаем, что Y = x i + e, где e – вектор ошибок.
Пусть τ – случайная величина, равная | e | (количество ошибок).
Т.к. так как относительно этой величины мы имеем распределение Бернулли, то E (τ) = np, D (τ) = np (1 – p).
Вводится некоторый параметр b =  , который носит чисто технический характер. Грубо говоря, если на одно слово приходится npошибок, то мы будем окружать кодовые слова шарами радиуса ρ =[np+b], где b>0 – некоторая «маленькая» добавка
, который носит чисто технический характер. Грубо говоря, если на одно слово приходится npошибок, то мы будем окружать кодовые слова шарами радиуса ρ =[np+b], где b>0 – некоторая «маленькая» добавка
Лемма ( ). Справедливо соотношение
). Справедливо соотношение
P { τ > ρ } ≤ ε \2
для любого заранее заданного ε.
Доказательство. Применим неравенство Чебышева:
P {| τ – E (τ)| > ε } ≤ D (τ)/ ε 2.
Положим ρ = [ E (τ) + b], тогда
P {| τ – np | >b} ≤ D (τ) / b 2.
Отсюда следует
P {| τ – np | > b } ≤ ε/ 2.
Тогда P (τ > ρ) = P {| τ – np | > b }. Это проиллюстрировано ниже:
- τnpτ
τ > nP + b
τ – nP > b
Отсюда следует P { τ > ρ }≤ P {| τ – np | >b}≤ D (τ) / b 2=ε/2.
Лемма доказана.
Лемма ( ): Пусть ρ = [ E (τ) + b ] и b =
): Пусть ρ = [ E (τ) + b ] и b =  , тогда
, тогда
1\ n log | Sρ (x)| ≤ H(P) +O(n -1\2) при n → ∞.
Доказательство.Из леммы ( ) и леммы (
) и леммы ( ) получаем неравенство:
) получаем неравенство:
| Sρ (x)| ≤ 2 nH (ρ \ n ).
Прологарифмируем и поделим на n, разложим логарифм в ряд (это корректно) и оставим главные члены:
1\ n log | Sρ (x)| ≤ H(ρ \ n) = - ρ \ n log ρ \ n – (1 – ρ \ n) log (1 – ρ \ n) = - [ nP + b ]\ n log [ nP + b ]\ n – (1 – [ nP + b ]\ n ] log (1 – [ nP + b ]\ n) ≈ - P log P – (1 – P) log (1 – P) +O(b \ n) = H(p)+ O(n -1\2).
Лемма доказана.
Замечание. В [9] доказано иное утверждение, но оно ошибочно, хотя это и невлияет на конечный результат.
Здесь и далее мы используем алгоритм декодирования на основе таблицы декодирования. Более того, подчеркнем, что ситуации 1 и 2 не противоречат друг другу!
Введем некоторую функцию, определенную на парах векторов из Bn.
 (f1)
(f1)
Лемма. Справедливо соотношение:
 (****)
(****)
Доказательство. Здесь P (xi) – вероятность неправильного декодирования переданного слова xi  Bn. P (y| xi) - вероятность того, что при передаче слова xi на декодер попало слово y. Пусть Q(y| xi)- вероятность того, слово y декодировано в слово xi. Тогда
Bn. P (y| xi) - вероятность того, что при передаче слова xi на декодер попало слово y. Пусть Q(y| xi)- вероятность того, слово y декодировано в слово xi. Тогда

Заметим, что слово y может быть декодировано в слово xj, только если оно попало в шар соответствующего радиуса с центром в xj. Из этого следует, что

Если xi декодируется правильно, то y попало в шар нужного радиусас центром в xi, и тогда  =0. В этом случае в неравенстве (****) слева 0, а справа неотрицательная величина.Если xi декодируется неправильно, то y попало в шар нужного радиусас центром в xj, j≠i, и тогда, если
=0. В этом случае в неравенстве (****) слева 0, а справа неотрицательная величина.Если xi декодируется неправильно, то y попало в шар нужного радиусас центром в xj, j≠i, и тогда, если  =0, то
=0, то

Если же  =1 (а это может быть, если шары пересекаются), то
=1 (а это может быть, если шары пересекаются), то

Лемма доказана.
Вторая теорема Шеннона.
Теорема (2-я теоремаШеннона). Для любого R: 0 < R < C (ρ), такого что M=2[nR], выполняется соотношение:
P *(M, n, P) → 0, n → ∞.
Доказательство. Пусть передаем x i, принято некое y, оцениваем ошибку декодирования.
Мы рассматриваем в качестве кодов все возможные подмножества Bn. Т.е. кодовые точки располагаются случайным образом. Точки упали как угодно, на них строим шары радиуса ρ.
Декодируем так: если точка у попала в шарик радиуса у вокруг кодовой точки, то декодируем ее в данную кодовую точку, если в этом шаре нет других точек; если есть другие кодовые точки или у не попало ни в один из шаров вокруг кодовой точки, то у декодируем по эвристическим правилам. При этом возможна ошибка декодирования.
Вспомним введенную выше функцию f(x,y). Из леммы (****) следует, что вероятность того, что у находится от x i на расстоянии, большем ρ, задается формулой:

С другой стороны, из леммы (**) следует, что эта вероятность P { τ > ρ } ≤ ε \2.
Таким образом
Pc = 1\ M ∑ P (xi)= 
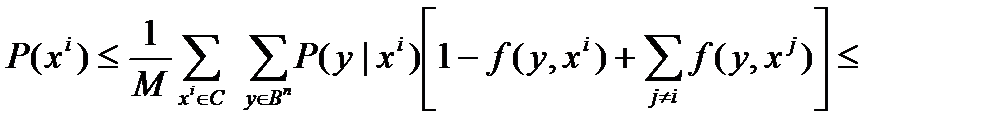
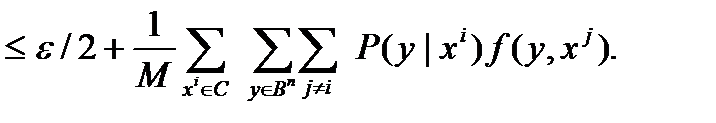
Заметим теперь, что E(f(y|xi)- математическое ожидание того, что у попал в шар с центром в x i, равно:
E(f(y|xi)=| Sρ (x)| / 2 n.
Теперь вспомним неравенство:
P *(M, n, p) ≤ 

Заметим теперь, что минимальное значение случайной величины не превосходит ее математического ожидания:
Minξ≤E(ξ).
Из этих соотношений следует цепочка неравенств.
P *(M, n, p) 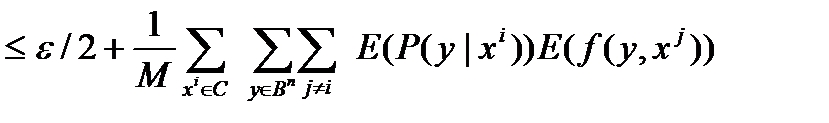 =
=
=  =
=  =
=
=  =
= 
Таким образом
P *(M, n, p) – ε \2≤ 
Вспомним, что 0 < R < C (ρ), M=2[nR].
Применяем лемму ( ) и соотношения: [nR] = log M, M = 2 Rn:
) и соотношения: [nR] = log M, M = 2 Rn:
1\ n log (P *(M, n, P) – ε \2) ≤ 1\ n log(| Sρ | M \2 n)= 1\ n log | Sρ |2 Rn - n ≤ R – C (ρ) – 1+O(n -1\2) + 1.
Пусть δ= C(P)-R. Тогда имеем при при больших n неравенство
P *(M, n, P) < ε \2 + 2- δn.
Устремляем n→∞ и δ→0. Получаем
P *(M, n, P) →0.
Теорема доказана.



 - вектор ошибок. Он подчиняется распределению Бернулли, поэтому матожидание и дисперсия такого вектора
- вектор ошибок. Он подчиняется распределению Бернулли, поэтому матожидание и дисперсия такого вектора  и D(ξ)=np(1-p).
и D(ξ)=np(1-p). b x 2
b x 2
 ). Возьмем точку в Bn и шар S[pn] (x), оценим число точек в нем. Справедливо неравенство
). Возьмем точку в Bn и шар S[pn] (x), оценим число точек в нем. Справедливо неравенство .
.
 ,
,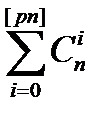 - мощность шара радиуса [pn].
- мощность шара радиуса [pn].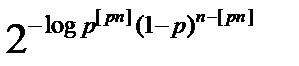 ≤ 2 nH ( p ).
≤ 2 nH ( p ). , который носит чисто технический характер. Грубо говоря, если на одно слово приходится npошибок, то мы будем окружать кодовые слова шарами радиуса ρ =[np+b], где b>0 – некоторая «маленькая» добавка
, который носит чисто технический характер. Грубо говоря, если на одно слово приходится npошибок, то мы будем окружать кодовые слова шарами радиуса ρ =[np+b], где b>0 – некоторая «маленькая» добавка ). Справедливо соотношение
). Справедливо соотношение ): Пусть ρ = [ E (τ) + b ] и b =
): Пусть ρ = [ E (τ) + b ] и b =  ) получаем неравенство:
) получаем неравенство: (f1)
(f1) (****)
(****) Bn. P (y| xi) - вероятность того, что при передаче слова xi на декодер попало слово y. Пусть Q(y| xi)- вероятность того, слово y декодировано в слово xi. Тогда
Bn. P (y| xi) - вероятность того, что при передаче слова xi на декодер попало слово y. Пусть Q(y| xi)- вероятность того, слово y декодировано в слово xi. Тогда

 =0. В этом случае в неравенстве (****) слева 0, а справа неотрицательная величина.Если xi декодируется неправильно, то y попало в шар нужного радиусас центром в xj, j≠i, и тогда, если
=0. В этом случае в неравенстве (****) слева 0, а справа неотрицательная величина.Если xi декодируется неправильно, то y попало в шар нужного радиусас центром в xj, j≠i, и тогда, если 



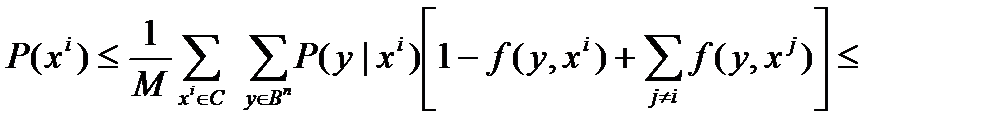
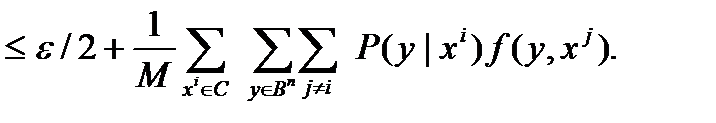


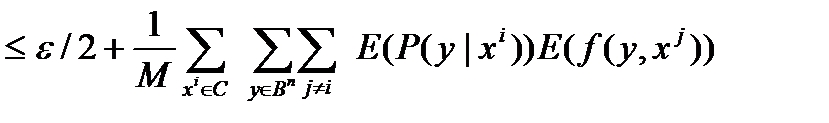 =
= =
=  =
= =
= 


