Средства, которыми мы теперь располагаем, достаточны для того, чтобы обратиться к детальному анализу систем линейных уравнений. Пусть дана система
 .
.
Введём в рассмотрение две матрицы: 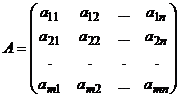 и
и 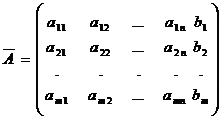 .
.
Первая матрица составлена из коэффициентов при неизвестных в системе (1) и называется основной, а вторая получается из неё добавлением столбца свободных членов и называется расширенной матрицей системы (1). Обозначим строки матрицы  через
через  , а строки матрицы
, а строки матрицы  через
через  . Поскольку строки матрицы
. Поскольку строки матрицы  являются «кусками» строк матрицы
являются «кусками» строк матрицы  , совершенно очевидно, что любая линейная зависимость между строками матрицы
, совершенно очевидно, что любая линейная зависимость между строками матрицы  влечёт за собой такую же точно зависимость между строками матрицы
влечёт за собой такую же точно зависимость между строками матрицы  :
:
 (2).
(2).
Очевидно, что уравнение вида  (3), не имеет решения. Т.к. всякая система уравнений, которая имеет уравнение вида (3) или в которой при помощи элементарных преобразований можно получить такие уравнения, будет несовместна.
(3), не имеет решения. Т.к. всякая система уравнений, которая имеет уравнение вида (3) или в которой при помощи элементарных преобразований можно получить такие уравнения, будет несовместна.
Теорема Кронекера-Капелли: (критерий совместности системы линейных уравнений) Системы линейных уравнений (1) совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной матрицы.
Доказательство: Приведём систему (1) к ступенчатому виду:
 ,
,  ,
,
 .
.
Тогда ступенчатые матрицы  и
и  соответственно будут основной и расширенной матрицами системы (4). Если система (4) несовместна, то это значит, что в ней имеется уравнение вида (3). Т.е. в матрице
соответственно будут основной и расширенной матрицами системы (4). Если система (4) несовместна, то это значит, что в ней имеется уравнение вида (3). Т.е. в матрице  имеется строка, в которой все элементы, кроме
имеется строка, в которой все элементы, кроме  , равны нулю; это значит, что число ненулевых строк в матрице
, равны нулю; это значит, что число ненулевых строк в матрице  будет на 1 больше, чем у матрицы
будет на 1 больше, чем у матрицы  . Так как матрицы ступенчатые, то ранги их равны числу строк, поэтому получаем, что ранг матрицы
. Так как матрицы ступенчатые, то ранги их равны числу строк, поэтому получаем, что ранг матрицы  равен
равен  , а ранг
, а ранг  равен
равен 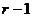 . С другой стороны, если система (4) совместна, то в ней нет уравнения вида (3), т.е. матрица
. С другой стороны, если система (4) совместна, то в ней нет уравнения вида (3), т.е. матрица  не имеет строки, в которой все элементы, кроме последнего, равны нулю, тогда число ненулевых строк в матрицах
не имеет строки, в которой все элементы, кроме последнего, равны нулю, тогда число ненулевых строк в матрицах  и
и  будут совпадать, что говорит о равенстве рангов этих матриц. Так как элементарные преобразования не меняют множества решений системы и ранг матрицы, то можно сказать, что система (1) совместна тогда и только тогда, когда
будут совпадать, что говорит о равенстве рангов этих матриц. Так как элементарные преобразования не меняют множества решений системы и ранг матрицы, то можно сказать, что система (1) совместна тогда и только тогда, когда  . Теорема доказана.
. Теорема доказана.
Глава VI. Теория определителей
Подстановки
Определение 1: Подстановкой множества  , где
, где  называется инъективное отображение множества М на себя.
называется инъективное отображение множества М на себя.
Другими словами, подстановкой из n элементов называется замена каждого элемента из множества М вполне определенным элементом из того же множества, причем так, что различные элементы заменяются различными элементами. Всякое отображение  множества М на себя удобно записать в виде таблицы
множества М на себя удобно записать в виде таблицы  .
.
Порядок чисел в первой строке этой таблицы несуществен, его можно как угодно изменить. Однако надо следить за тем, чтобы для всякого  число
число  было записано непосредственно под
было записано непосредственно под  . Например:
. Например:  или
или  . Строки подстановки
. Строки подстановки  называются перестановками элементов множества
называются перестановками элементов множества  .
.
Множество всех подстановок множества М обозначим через S n; элементы этого множества называются подстановками степени п.
Произведение  двух подстановок
двух подстановок  и
и  множества М определяется как композиция отображений,
множества М определяется как композиция отображений,  и
и  , т.е. их последовательное выполнение. Таким образом, по определению
, т.е. их последовательное выполнение. Таким образом, по определению  для
для  .
.
Обозначим через  тождественное отображение М на себя:
тождественное отображение М на себя:  для
для  , т.е.
, т.е.  .
.
Легко видеть, что для любой подстановки 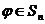
 , т.е.
, т.е. 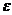 является нейтральным элементом относительно умножения.
является нейтральным элементом относительно умножения.
Если  - подстановка множества М, то
- подстановка множества М, то  - также подстановка множества М и
- также подстановка множества М и  . При этом
. При этом  .
.
Теорема 1: Алгебра подстановок n -ой степени  является группой.
является группой.
Докажите самостоятельно.
Определение 2: Группа всех подстановок n- ой степени  - называется симметрической группой степени
- называется симметрической группой степени  . Тождественная подстановка
. Тождественная подстановка 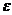 называется единичным элементом этой группы.
называется единичным элементом этой группы.
Пусть дана подстановка 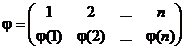 множества
множества  ,
,  - элементы множества
- элементы множества  . Говорят, что числа
. Говорят, что числа  образуют инверсию в строке подстановки, если
образуют инверсию в строке подстановки, если  , но
, но  стоит в этой строке раньше
стоит в этой строке раньше 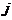 . Подстановка называется чётной, если суммарноечисло инверсий в обеих строках подстановки чётно, и нечётной в противном случае.
. Подстановка называется чётной, если суммарноечисло инверсий в обеих строках подстановки чётно, и нечётной в противном случае.
Так, например, в подстановке  нет инверсий, она чётная, а в подстановке
нет инверсий, она чётная, а в подстановке  одна инверсия и она нечётная.
одна инверсия и она нечётная.
Если в любой строке подстановки любые два числа  и
и 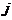 поменять местами, то её чётность измениться на противоположную. Например, поменяем в подстановке
поменять местами, то её чётность измениться на противоположную. Например, поменяем в подстановке  2 и 1 в нижней строке. Получим подстановку
2 и 1 в нижней строке. Получим подстановку 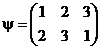 , в которой две инверсии, и она чётная.
, в которой две инверсии, и она чётная.
Рассмотрим теперь частный, но важный случай подстановки. Назовем подстановку  из чисел
из чисел 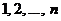

 -членной циклической или
-членной циклической или  - членным циклом, если она
- членным циклом, если она  переводит в число
переводит в число  , отличное от
, отличное от 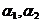 - в число
- в число  , отличное от
, отличное от 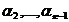 - в число
- в число  , и
, и  - в исходное число
- в исходное число 
 , а прочие числа (при
, а прочие числа (при  ) оставляет неизменными. Циклическая подстановка обычно обозначается символом
) оставляет неизменными. Циклическая подстановка обычно обозначается символом  .
.
Нетрудно убедиться, что всякую подстановку из чисел  можно представить как произведение независимых циклов. Независимых в том смысле, что никакие два цикла разложения не имеют общих чисел.
можно представить как произведение независимых циклов. Независимых в том смысле, что никакие два цикла разложения не имеют общих чисел.
Для наглядности обратимся к конкретному примеру.


 или
или 
Теорема 2: Разность P между степенью n подстановки числом s независимых циклов (включая и одиночные), на которые разлагается данная подстановка, имеет ту же четность, что и данная подстановка из  элементов. Т. е.
элементов. Т. е. 
Без доказательства.
Примеры:  ,
,  = 6 – 3 = 3; значит подстановка
= 6 – 3 = 3; значит подстановка  - нечетна.
- нечетна.
Обозначим через  знак подстановки
знак подстановки  , тогда
, тогда
 .
.
Можно сказать, что  , где
, где  , или
, или  , где
, где  и
и  - числа инверсий в верхней и нижней строках подстановки
- числа инверсий в верхней и нижней строках подстановки  .
.
Теорема 3: Произведение двух (или четного числа) подстановок одинаковой четности есть четная подстановка.
Теорема 4: Произведение двух подстановок различной четности есть нечетная подстановка.
Теоремы 3 и 4 желательно, но не обязательно, доказать самостоятельно.
Следствие: Подстановки  и
и  имеют одинаковую чётность.
имеют одинаковую чётность.
Действительно,  , а
, а  - чётная подстановка.
- чётная подстановка.
§ 2. Определители
Определение 1: Матрица, у которой число строк равно числу столбцов, называется квадратной. Число строк (столбцов) квадратной матрицы называется её порядком. Диагональ, образованная элементами  , называется главной диагональю.
, называется главной диагональю.
Определение 2: Определителем (или детерминантом) n –го порядка квадратной матрицы А называется алгебраическая сумма всевозможных членов, представляющих собой произведение n элементов, взятых по одному и только по одному из каждой строки и каждого столбца матрицы со знаком, совпадающим со знаком подстановки образованной индексами элементов.
Если
 ,
,
то ее определитель обозначается
 .
.
Примеры: Если  , то
, то 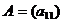 и
и  . Если
. Если  , то
, то  ,
,  .
.
Если  , то
, то  .
.
Предложение 1: Определитель матрицы с нулевой строкой (столбцом) равен нулю.
Квадратная матрица называется диагональной, если равны нулю все ее элементы, расположенные вне главной диагонали.
Предложение 2: Определитель диагональной матрицы равен произведению элементов ее главной диагонали.
Квадратная матрица называется треугольной, если равны нулю все ее элементы, расположенные выше (ниже) главной диагонали.
Предложение 3: Определитель треугольной матрицы равен произведению диагональных элементов.
Свойства определителей
1. Значение определителя  порядка не изменится, если его строки заменить столбцами, сохраняя порядок следования.
порядка не изменится, если его строки заменить столбцами, сохраняя порядок следования.
Операция замены в определителе строк столбцами с сохранением порядка следования называется транспонированием определителя. Таким образом, в свойстве 1 утверждается, что от транспонирования значение определителя не изменится.
Доказательство: Нам надо показать, что определители
 равны.
равны.
Пусть  (1) – произвольный член определителя
(1) – произвольный член определителя  . Очевидно, что элементы члена (1) будут также находиться по одному и только по одному в каждой строке и каждом столбце определителя
. Очевидно, что элементы члена (1) будут также находиться по одному и только по одному в каждой строке и каждом столбце определителя  . Следовательно, (1) есть вместе с тем и член определителя
. Следовательно, (1) есть вместе с тем и член определителя  . Аналогично, каждый член определителя
. Аналогично, каждый член определителя  является членом и определителя
является членом и определителя  . Далее, если снова (1) – член определителя
. Далее, если снова (1) – член определителя  , то этот член входит в определитель
, то этот член входит в определитель  со знаком
со знаком 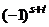 , где
, где  - число инверсий в строках подстановки
- число инверсий в строках подстановки  . В определителе
. В определителе  знак члена (1) совпадает со знаком подстановки
знак члена (1) совпадает со знаком подстановки  . Но
. Но  . Откуда следует, что
. Откуда следует, что 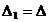 .
.
Это свойство иногда называют свойством равноправности строк и столбцов определителя.
2. Определитель n –го порядка, у которого две строки (два столбца) одинаковы, равен нулю.
Доказательство: Пусть у определителя  n –го порядка одинаковы
n –го порядка одинаковы  -я и
-я и  -я строки:
-я строки:
 ,
,  .
.
Возьмем произвольный член определителя
 (2).
(2).
Знак этого члена равен (-1)t, где t – число инверсий в подстановке 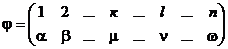 . Наряду с членом (2) рассмотрим член
. Наряду с членом (2) рассмотрим член  (4)
(4)
того же определителя. Член (3) равен члену (2), так как в силу совпадения  -я и
-я и  -я строк
-я строк 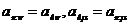 .
.
Однако член (3) входит в определитель  со знаком, противоположным знаку члена (2). Действительно, знак члена (4) равен
со знаком, противоположным знаку члена (2). Действительно, знак члена (4) равен  , где
, где  - число инверсий в подстановке
- число инверсий в подстановке
 ,
,
которая получается из подстановки  перестановкой чисел
перестановкой чисел  и
и  в нижней строке. Чётности перестановок
в нижней строке. Чётности перестановок  и
и  противоположны. Следовательно, t и
противоположны. Следовательно, t и  – числа различной четности и потому знак
– числа различной четности и потому знак  противоположен знаку
противоположен знаку  .
.
Поскольку члены (2) и (3) равны, но имеют противоположные знаки, они должны в определителе  уничтожаться. Таким образом, получается попарное уничтожение всех членов определителя, вследствие чего
уничтожаться. Таким образом, получается попарное уничтожение всех членов определителя, вследствие чего  .
.
Справедливость свойства 2 для столбцов следует из равноправности строк и столбцов определителя.
3. Если все элементы какого-нибудь столбца (строки) определителя n –го порядка умножить на одно и то же число m, то значение определителя умножится на m.
Доказательство: Умножим, например, элементы 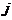 -го столбца определителя
-го столбца определителя 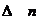 -го порядка на
-го порядка на 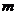 . Тогда элементы
. Тогда элементы 
 этого столбца превратятся в
этого столбца превратятся в  . Если до умножения каждый член определителя имел вид:
. Если до умножения каждый член определителя имел вид:  , то после умножения он примет вид:
, то после умножения он примет вид:  , т.е. умножится на
, т.е. умножится на 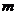 . Что касается знака, то до и после умножения член должен иметь один и тот же знак
. Что касается знака, то до и после умножения член должен иметь один и тот же знак  , где
, где  - число инверсий в подстановке
- число инверсий в подстановке  .
.
4. Если все элементы какого-нибудь столбца (строки) определителя n –го порядка обладают общим множителем, то его можно вынести за знак определителя.
Пример: 

Здесь вынесли за знак определителя общий множитель 2 элементов третьего столбца.
Свойство 4 непосредственно вытекает из свойства 3.
5. Определитель п –го порядка, у которого элементы двух строк (столбцов) соответственно пропорциональны, равен нулю.
Доказательство: Пусть, например, пропорциональны  -я и
-я и  -я строки определителя
-я строки определителя  . Это значит, что каждый элемент
. Это значит, что каждый элемент  -й строки отличается от соответствующего элемента
-й строки отличается от соответствующего элемента  -й строки на один и тот же множитель
-й строки на один и тот же множитель 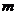 , т.е. определитель выглядит так:
, т.е. определитель выглядит так:

Если теперь на основании свойства 4 вынести общий множитель 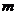 за знак определителя, то получится определитель с двумя одинаковыми строками. Такой определитель согласно свойству 2 равен нулю.
за знак определителя, то получится определитель с двумя одинаковыми строками. Такой определитель согласно свойству 2 равен нулю.
6. Пусть каждый элемент  -й строки (столбца) определителя n –го порядка
-й строки (столбца) определителя n –го порядка  есть сумма двух слагаемых. Тогда определитель
есть сумма двух слагаемых. Тогда определитель  равен сумме двух определителей того же порядка, причем в одном определителе
равен сумме двух определителей того же порядка, причем в одном определителе  -я строка (столбец) состоит из первых слагаемых, а в другом – из вторых слагаемых. Остальные строки (столбцы) того и другого определителя те же, что и в определителе
-я строка (столбец) состоит из первых слагаемых, а в другом – из вторых слагаемых. Остальные строки (столбцы) того и другого определителя те же, что и в определителе  .
.
Доказательство: Пусть в определителе

каждый элемент  -й строки есть сумма двух слагаемых:
-й строки есть сумма двух слагаемых:  .
.
Обратимся к произвольному члену определителя: 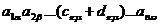 . Он имеет знак знака подстановки
. Он имеет знак знака подстановки  . Раскроем скобки; тогда наш член распадается на два члена:
. Раскроем скобки; тогда наш член распадается на два члена: 
Но произведение  есть член определителя
есть член определителя  и входит в него со знаком, определяющимся подстановкой
и входит в него со знаком, определяющимся подстановкой  . Произведение
. Произведение  есть член определителя
есть член определителя  и входит в него с таким же знаком. Отсюда справедливость свойства 6 становится очевидной:
и входит в него с таким же знаком. Отсюда справедливость свойства 6 становится очевидной:  , где
, где
 ,
,  .
.
Пользуясь методом математической индукции, нетрудно свойство 6 распространить на случай любого числа слагаемых.
7. Определитель n –го порядка не меняет своего значения от прибавления ко всем элементам какой-нибудь строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Доказательство: Прибавим к элементам  -й строки определителя
-й строки определителя  соответствующие элементы
соответствующие элементы  -й строки того же определителя, умноженные на число
-й строки того же определителя, умноженные на число 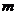 . Имеем:
. Имеем:

Мы видим, что каждый элемент  -й строки определителя
-й строки определителя  является суммой двух слагаемых. Отсюда по свойству 6
является суммой двух слагаемых. Отсюда по свойству 6
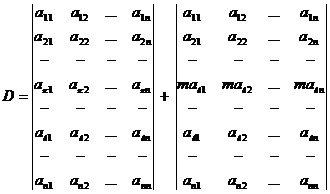 .
.
Первый определитель этой суммы есть  , а второй равен нулю, так как у него две строки пропорциональны. Следовательно,
, а второй равен нулю, так как у него две строки пропорциональны. Следовательно,  , что и требовалось показать.
, что и требовалось показать.
Свойство 7, как мы увидим впоследствии, значительно упрощает вычисление определителей.
8. Если поменять местами две строки (столбца) определителя n –го порядка, то определитель изменит знак на противоположный, а по абсолютной величине не изменится.
Доказательство: Подвергнем определитель

следующим преобразованиям. Прибавим к его  -й строке
-й строке 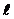 -ю. Получим:
-ю. Получим:
 .
.
В определителе  из
из  - й строки вычтем
- й строки вычтем  -ю строку. Получим:
-ю строку. Получим:
 .
.
Наконец, прибавим в определителе 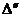 к
к  -й
-й  - ю. Получим:
- ю. Получим:  .
.
Все эти преобразования по свойству 7 не изменяют значения определителя. Следовательно  ,
,
что и требовалось доказать.



 .
.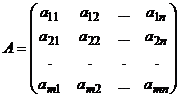 и
и 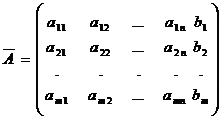 .
. через
через  , а строки матрицы
, а строки матрицы  через
через  . Поскольку строки матрицы
. Поскольку строки матрицы  (2).
(2). (3), не имеет решения. Т.к. всякая система уравнений, которая имеет уравнение вида (3) или в которой при помощи элементарных преобразований можно получить такие уравнения, будет несовместна.
(3), не имеет решения. Т.к. всякая система уравнений, которая имеет уравнение вида (3) или в которой при помощи элементарных преобразований можно получить такие уравнения, будет несовместна. ,
,  ,
, .
. и
и  соответственно будут основной и расширенной матрицами системы (4). Если система (4) несовместна, то это значит, что в ней имеется уравнение вида (3). Т.е. в матрице
соответственно будут основной и расширенной матрицами системы (4). Если система (4) несовместна, то это значит, что в ней имеется уравнение вида (3). Т.е. в матрице  , равны нулю; это значит, что число ненулевых строк в матрице
, равны нулю; это значит, что число ненулевых строк в матрице  , а ранг
, а ранг 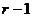 . С другой стороны, если система (4) совместна, то в ней нет уравнения вида (3), т.е. матрица
. С другой стороны, если система (4) совместна, то в ней нет уравнения вида (3), т.е. матрица  . Теорема доказана.
. Теорема доказана. , где
, где  называется инъективное отображение множества М на себя.
называется инъективное отображение множества М на себя. множества М на себя удобно записать в виде таблицы
множества М на себя удобно записать в виде таблицы  .
. число
число  было записано непосредственно под
было записано непосредственно под  или
или  . Строки подстановки
. Строки подстановки  называются перестановками элементов множества
называются перестановками элементов множества  .
. двух подстановок
двух подстановок  множества М определяется как композиция отображений,
множества М определяется как композиция отображений,  для
для  .
. тождественное отображение М на себя:
тождественное отображение М на себя:  для
для  .
.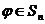
 , т.е.
, т.е. 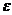 является нейтральным элементом относительно умножения.
является нейтральным элементом относительно умножения. - также подстановка множества М и
- также подстановка множества М и  . При этом
. При этом  .
. является группой.
является группой. . Тождественная подстановка
. Тождественная подстановка 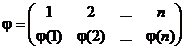 множества
множества  ,
,  - элементы множества
- элементы множества  , но
, но  стоит в этой строке раньше
стоит в этой строке раньше 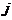 . Подстановка называется чётной, если суммарноечисло инверсий в обеих строках подстановки чётно, и нечётной в противном случае.
. Подстановка называется чётной, если суммарноечисло инверсий в обеих строках подстановки чётно, и нечётной в противном случае. нет инверсий, она чётная, а в подстановке
нет инверсий, она чётная, а в подстановке  одна инверсия и она нечётная.
одна инверсия и она нечётная.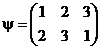 , в которой две инверсии, и она чётная.
, в которой две инверсии, и она чётная.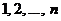

 переводит в число
переводит в число  , отличное от
, отличное от 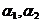 - в число
- в число  , отличное от
, отличное от 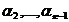 - в число
- в число  , и
, и  - в исходное число
- в исходное число  , а прочие числа (при
, а прочие числа (при  ) оставляет неизменными. Циклическая подстановка обычно обозначается символом
) оставляет неизменными. Циклическая подстановка обычно обозначается символом  .
. можно представить как произведение независимых циклов. Независимых в том смысле, что никакие два цикла разложения не имеют общих чисел.
можно представить как произведение независимых циклов. Независимых в том смысле, что никакие два цикла разложения не имеют общих чисел.
 или
или 

 ,
,  знак подстановки
знак подстановки  .
. , где
, где  , где
, где  и
и  - числа инверсий в верхней и нижней строках подстановки
- числа инверсий в верхней и нижней строках подстановки  имеют одинаковую чётность.
имеют одинаковую чётность. , а
, а  - чётная подстановка.
- чётная подстановка. , называется главной диагональю.
, называется главной диагональю. ,
, .
. , то
, то 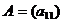 и
и  . Если
. Если  , то
, то  ,
,  .
. , то
, то  .
. равны.
равны. (1) – произвольный член определителя
(1) – произвольный член определителя  . Очевидно, что элементы члена (1) будут также находиться по одному и только по одному в каждой строке и каждом столбце определителя
. Очевидно, что элементы члена (1) будут также находиться по одному и только по одному в каждой строке и каждом столбце определителя  . Следовательно, (1) есть вместе с тем и член определителя
. Следовательно, (1) есть вместе с тем и член определителя  является членом и определителя
является членом и определителя 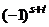 , где
, где  - число инверсий в строках подстановки
- число инверсий в строках подстановки  . В определителе
. В определителе  . Но
. Но  . Откуда следует, что
. Откуда следует, что 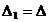 .
. -я строки:
-я строки: ,
,  .
. (2).
(2).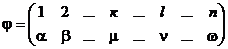 . Наряду с членом (2) рассмотрим член
. Наряду с членом (2) рассмотрим член  (4)
(4)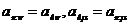 .
. , где
, где  - число инверсий в подстановке
- число инверсий в подстановке ,
, и
и  в нижней строке. Чётности перестановок
в нижней строке. Чётности перестановок  противоположны. Следовательно, t и
противоположны. Следовательно, t и  .
. .
.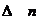 -го порядка на
-го порядка на 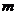 . Тогда элементы
. Тогда элементы  этого столбца превратятся в
этого столбца превратятся в  . Если до умножения каждый член определителя имел вид:
. Если до умножения каждый член определителя имел вид:  , то после умножения он примет вид:
, то после умножения он примет вид:  , т.е. умножится на
, т.е. умножится на  .
.


 .
.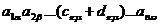 . Он имеет знак знака подстановки
. Он имеет знак знака подстановки  . Раскроем скобки; тогда наш член распадается на два члена:
. Раскроем скобки; тогда наш член распадается на два члена: 
 есть член определителя
есть член определителя  есть член определителя
есть член определителя  и входит в него с таким же знаком. Отсюда справедливость свойства 6 становится очевидной:
и входит в него с таким же знаком. Отсюда справедливость свойства 6 становится очевидной:  , где
, где ,
,  .
. -й строки того же определителя, умноженные на число
-й строки того же определителя, умноженные на число 
 является суммой двух слагаемых. Отсюда по свойству 6
является суммой двух слагаемых. Отсюда по свойству 6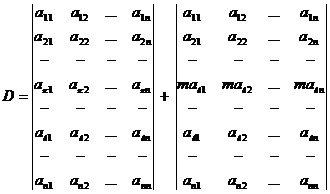 .
. , что и требовалось показать.
, что и требовалось показать.
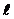 -ю. Получим:
-ю. Получим: .
. из
из  .
.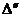 к
к  -й
-й  .
. ,
,


