

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Параметрически заданной называется функция y=y(x), если она возникла с помощью соотношений
 ,tÎT.
,tÎT.
Производная функции, заданной параметрически, находится по формуле:

Чтобы отыскать вторую производную, используем эту формулу 2 раза.
Производная по направлению.
Пусть даны скалярная функция f(M)=f(x1,x2,…,xn) векторного аргумента, ненулевой вектор а и фиксированная точка М0.
Тогда производной от функции f(M) в направлении вектора а в точке М0 называется предел 
и обозначается  , при этом знак выбираем знак «+», если вектор M0Ma,
, при этом знак выбираем знак «+», если вектор M0Ma,
«-», если M0M¯a.
Кривизна графика фун-и в точке М0 – число k, определяемое равенством  ,
,
Где w- угол между касательными в точках М и М0,
а s - длина дуги.
Уравнение касательной плоскости и нормали к поверхности.
Уравнение касательной для функции, заданной:
· В явной форме:

· В неявной форме:
 или
или 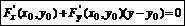
· Для параметрически заданной функции:
 tÎ(t1,t2) или
tÎ(t1,t2) или 
при t=t0,x0=x(t0),y0=(t0), 
· В случае пространственной кривой, заданной параметрически  :
:
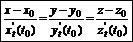
Нормаль к кривой – прямая, перпендикулярная касательной и проходящая через точку касания.
· При задании кривой неявно уравнением F(x,y)=0 ур-е нормали в точке (x0,y0) можно записать в виде:
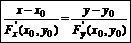
Касательная плоскость к поверхности S в точке М0 – плоскость П, проходящая через точку М0 и содержащая касательные ко всем кривым, проходящим через М0 и лежащим на поверхности S в точке М0.
· Уравнение касательной плоскости к поверхности F(x,y,z) = 0 в точке М0(х0, у0, z0) можно записать в виде:

· Если поверхность S задана явно ур-м z=f(x,y), то ур-е касательной имеет вид:

· Уравнение нормали к поверхности F(x,y,z) в точке М0(х0,y0,z0) можно записать в виде:

Дифференциал функции.
|
|
Дифференциал высшего порядка
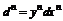
33. Формула Тейлора.
Если f – скалярная фун-я одной или многих переменных, имеющая непрерывные производные до порядка (n+1) включительно, то ее приращение в точке х0, вызванное приращением аргумента Dх, можно представить в виде:
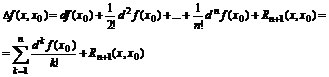 Эта формула применяется для вычисления приближенных значений.
Эта формула применяется для вычисления приближенных значений.
Формула Лагранжа.
 , где с – точка, лежащая между х и х0.
, где с – точка, лежащая между х и х0.
Формула Маклорена.
При х=х0 формула Тейлора называется формулой Маклорена.
Основные теоремы дифференциального исчисления.
Теорема1.
Пусть функция f имеет в точке х0 конечную производную f’(x0).
Если f’(x0)>0 то существует окрестность U(x0) этой точки такая, что f(x)>f(x0) для любого х Î U+(х0) (из правосторонней окрестности).
f(x)<f(x0) для любого х Î U-(х0) (из левосторонней окрестности).
При f’(x0)<0 выполняются противоположные неравенства.
Точка наибольшего или наименьшего значения функции f(x) в области Х – точка х0 (хÎХ), для всех хÎХ которых выполняется неравенство:
f(x)£f(x0) (f(x)³f(x0).
Теорема Ферма. Пусть фун-я f(x) определена на промежутке (a,b) и в точке с этого промежутка принимает наибольшее или наименьшее значения. Тогда, если существует f’(c), то f’(c)=0.
Теорема Ролля. Если:
1) f(x) определена и непрерывна на отрезке [a,b]
2) существует конечная производная f’(x) на (а,b)
3) f(a)=f(b), то существует такая точка с, a<c<b что f’(c)=0.
Теорема Лагранжа. Если:
1) f(x) определена и непрерывна на отрезке [a,b]
2) существует конечная производная f’(x) на (a,b),то найдется такая точка с, a<c<b, что

Теорема Коши. Если:
1) функции f(x) и g(x) определены и непрерывны на [a,b]
2) существуют конечные производные f’(x) и g’(x) на (a,b)
3) g’(x)¹0 для всех х Î (a,b),
то существует точка с Î (a,b) такая, что 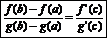
Теорема6. Если функция f(x) имеет в точке х конечную производную f’(x), то фун-я f дифференцируема в этой точке.
Теорема7. Если функция f(x) имеет в то х конечную производную и эта производная непрерывна в этой точке, то функция f дифференцируема в этой точке.
|
|
Правило Лапиталя.
Если:
1) функции f(x) и g(x) определены на (a,b)
2) 
3) всюду на (a,b) существуют производные f’(x) и g’(x) причем g’(x)¹0
4) существует предел 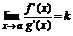 , то существует и предел
, то существует и предел 
Теорема Лапиталя2. Если:
1) функции f(x) и g(x) определены на (a,b)
2) 
3) всюду на (a,b) существуют производные f’(x) и g’(x), причем g’(x)¹0
4) существует предел  , то существует и предел
, то существует и предел  .
.
|
|
|

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!