Газ обладает упругостью. В твердом теле могут возникать нормальные и касательные напряжения, поэтому возможны волны продольные и поперечные.
В газах (жидкостях) нет касательных напряжений, и волны могут быть только продольные. Волны в газе (жидкости) представляют собой чередующиеся и распространяющиеся сжатия и разрежения.
Упругие продольные волны с частотой 20 – 20 000 Гц – звук, с частотой < 20 Гц – инфразвук, с частотой > 20 000 Гц – ультразвук.
Получим волновое уравнение.
Будем считать газ некоторой сплошной упругой средой с равновесными характеристиками:  .
.
Важные свойства:
1) При относительном смещении разных слоев газа возникают сжатия и разряжения.
2) Процессы сжатия и разряжения сопровождаются изменением давления (при сжатии давление повышается, при разряжении - снижается).
Неравенство давления приводит к макроскопическому движению.  .
.
В этом случае возникнет одномерная продольная волна. Сжатие и разряжение приводит к изменению давления, оно зависит от плотности и температуры. Если газ идеальный то 
Буден считать, что давление будет однозначной функцией плотности. Основание: отклонение от положения равновесия мало, тогда:
Случай А. Процессы сжатия и разряжения происходят достаточно медленно, поэтому температуры в разных слоях газа успевают выравниться, тогда процесс сжатия и разряжения можно считать изотермическим.

Случай Б. Теплопроводность газа крайне мала, процессы сжатия и разряжения происходят достаточно быстро, поэтому эти процессы можно считать адиабатическими, и изменения температуры будет локальным и тоже зависит от плотности.

И в случае Б давление является однозначной функцией плотности.
Это два предельных случая, рассматриваемый нами случай находится между этими случаями.
Выберем некоторый цилиндрический объем.
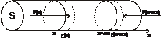 Масса газа, находящегося в этом объеме, равна:
Масса газа, находящегося в этом объеме, равна:

Конечно, происходит обмен веществом между объемом и окружающим пространством, но в среднем масса этого элемента остается постоянной.
Пусть происходит отклонение от равновесного положения, давление отклонилось от равновесного значения.
 – смещение левой границы.
– смещение левой границы.
 по сравнению с характерными размерами области сжатия и разряжения.
по сравнению с характерными размерами области сжатия и разряжения.
При этом предположении разница давлений слева и справа будет зависеть только от  . Масса слоя не измениться.
. Масса слоя не измениться.

 – отклонение от равновесия в окрестности
– отклонение от равновесия в окрестности  в заданный момент времени.
в заданный момент времени.



Случай А.

Случай Б.
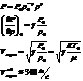

Энергия упругой волны. Плотность энергии. Вектор Умова.
Плотность потока энергии.
Рассмотрим продольную волну в твердом теле.
Равновесные характеристики:  .
.
 – смещение.
– смещение.
 – скорость смещения.
– скорость смещения.
 – относительная деформация.
– относительная деформация.


- плотность кинетической энергии.
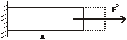


Растянутый стержень обладает упругой энергией:

- плотность энергии, локализованной в данном элементе:

Энергия может переноситься.
Найдем выражение для плотности потока энергии.


За время  силы
силы  и
и  совершают работу.
совершают работу.


 – плотность потока энергии.
– плотность потока энергии.

 – вектор Умова.
– вектор Умова.
Стоячие волны.
Принцип суперпозиции: Если одно и тоже вещество колеблется одновременно по двум различным законам, то в итоге суммарное колебание будет равно сумме различных колебаний.
Пусть распространяются две волны в одной и той же среде:
 .
.
Т.е. у них одинаковы модули но противоположны направления волновых скоростей. По принципу суперпозиции:
 .
.
Построим изображение данной волны в некоторые моменты времени (сфотографируем волну).

Попробуем найти такие  , что
, что 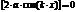 , это будут
, это будут  .
.
Фазовая скорость такой волны будет равна нулю. Выберем поверхность равной фазы в некотором  , где
, где 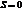 или
или  , но эти точки не подвижны.
, но эти точки не подвижны.
Опр.: Такая волна, фазовая скорость которой равна нулю, называется стоячей.
Вопрос: Но ведь фазовая скорость определяется формулой  , почему же она равна нулю?
, почему же она равна нулю?
Ответ: Это выражение справедливо для волн вида  , а у нас другой вид волн, поэтому фазовую скорость мы находим по определению.
, а у нас другой вид волн, поэтому фазовую скорость мы находим по определению.
Упругие волны в среде.
Пусть у нас есть гитарная струна, мы возбуждаем в ней некоторые колебания (щипком или ударом). В струне возбуждаются волны.
Запишем для струны волновое уравнение.
Пусть выбран малый кусок струны (малый настолько, что его можно аппроксимировать куском прямой). Пусть струна однородна и её плотность равна  . Запишем волновое уравнение как второй закон Ньютона. (т.к. в колебании нет переноса массы, то колебание идёт вдоль оси
. Запишем волновое уравнение как второй закон Ньютона. (т.к. в колебании нет переноса массы, то колебание идёт вдоль оси  ).
).

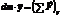 .
.
На кусочек свободно колеблющейся струны действуют три силы: две со стороны других кусков и сила тяжести.
Если гитару положить плашмя на колени, то сила тяжести будет перпендикулярна колебаниям.  - силы со стороны других кусков равны по модулю. Тогда:
- силы со стороны других кусков равны по модулю. Тогда:
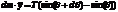 ,
,
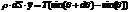 ,
,
где  - длина колеблющегося кусочка струны. Пусть величина отклонения струны мала по сравнению с длиной всей струны. Тогда можно записать следующие выражения:
- длина колеблющегося кусочка струны. Пусть величина отклонения струны мала по сравнению с длиной всей струны. Тогда можно записать следующие выражения:
 ,
,
 - дифференциал длины дуги, т.к.
- дифференциал длины дуги, т.к.  то
то  мала и
мала и  .
.
В силу того предположения имеем, что угол 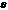 мал, откуда имеем:
мал, откуда имеем:
 .
.
Т.о. при подстановке имеем:
 ,
,
 - уравнение движения кусочка струны, откуда
- уравнение движения кусочка струны, откуда 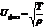 .
.
Будем считать, что оба конца струны зафиксированы, т.е.  .
.

Попробуем найти решения имеющие вид стоячих волн:
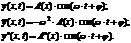 Подставим эти выражения в волновое уравнение, тогда:
Подставим эти выражения в волновое уравнение, тогда:
 ,
,
откуда имеем
 .
.
Получили линейное однородное дифференциальное уравнение с постоянными коэффициентами:

Где  - константы интегрирования. Найдем их из начальных условий:
- константы интегрирования. Найдем их из начальных условий:
 .
.
Т.к. 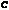 не равно нулю (т.к. тогда не будет никаких волн вообще), то имеем, что
не равно нулю (т.к. тогда не будет никаких волн вообще), то имеем, что

 .
.
Это означает, что  не может быть каким угодно, а они существуют только при определённых дискретных
не может быть каким угодно, а они существуют только при определённых дискретных  .
.
Запишем различные колебания при различных  :
:
 .
.
Т.о. общий вид подобного частного решения:
 ,
,
т.к. сумма частных решений тоже решение, то просуммируем подобные решения и посмотрим, что получится.
Зададим некоторое Н.У.  .
.
 - сфотографировали при
- сфотографировали при  , это уравнение показывает начальное положение струны, её начальную форму.
, это уравнение показывает начальное положение струны, её начальную форму.
 - скорость по
- скорость по  кусочка струны, показывает силу приложенную в начале.
кусочка струны, показывает силу приложенную в начале.
Запишем начальные условия в следующем виде:

Где

Откуда

Т.е. зная 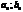 найдём
найдём  .
.
Волновое уравнение имеет бесконечное множество решений. Ранее нами было получено волновое уравнение для стоячей волны.
Пусть функция  определяет форму струны в начальный момент времени. Итак, нам известны две функции
определяет форму струны в начальный момент времени. Итак, нам известны две функции

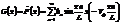 ,
,
где  - фазовая скорость. Нам необходимо найти
- фазовая скорость. Нам необходимо найти  и
и  .
.
Умножим слева и справа (1) на  и проинтегрируем от
и проинтегрируем от  до
до  .
.
 В правой части суммирование и интегрирование идет по разным переменным, поэтому можно преобразовать выражение.
В правой части суммирование и интегрирование идет по разным переменным, поэтому можно преобразовать выражение.
 Все интегралы
Все интегралы  равны нулю кроме случая
равны нулю кроме случая 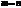 .
.


 аналогично можно найти и
аналогично можно найти и  .
.
Теперь, зная  и
и  , из системы
, из системы  можно легко найти
можно легко найти  и
и  .
.
Пример: струну оттянули и отпустили, так что ее начальная форма имеет следующий вид:
 ,
,  при
при  .
.
Функции 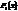 и
и  - линейные, причем
- линейные, причем
 ,
, 


 ,
, 




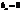 .
.
Теперь вычислим  Проинтегрировав по частям, получим
Проинтегрировав по частям, получим  . В нашем случае
. В нашем случае  ,
,  ,
, 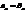 . Введем обозначения
. Введем обозначения 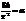 и рассмотрим несколько первых членов
и рассмотрим несколько первых членов  .
.
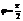 ,
,  ,
,  ,
,  ,
,  ,
,  , …
, …
Теперь запишем общее решение:

Величины слагаемых убывают, как  . Если струну оттянули слабо, то
. Если струну оттянули слабо, то  мало, и можно ограничиться первым слагаемым:
мало, и можно ограничиться первым слагаемым:  .
.
Мы видим, что  не зависит от
не зависит от  . Это можно объяснить тем, что
. Это можно объяснить тем, что 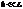 .
.
Электромагнитные волны.
Преобразуем уравнения Максвелла так, чтобы они приняли вид волнового уравнения. Запишем уравнения Максвелла в системе единиц СГСЕ
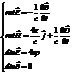
Рассмотрим случай, когда есть поле, но нет токов, и нет свободных зарядов. Пусть среда линейная и изотропная, тогда 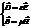 и уравнения Максвелла теперь выглядят так:
и уравнения Максвелла теперь выглядят так:
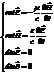
Учитывая, что

можно записать следующее соотношение: 
Но с другой стороны

сравнивая эти два соотношения, видим, что  .
.
Для вектора 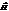 можно провести те же самые рассуждения
можно провести те же самые рассуждения  .
.
Итак, у нас получилось, что в пространстве, где нет токов, и нет свободных зарядов, может существовать волновое поле, даже в вакууме, где  .
.
Из полученных нами волновых уравнений для векторов  и
и 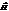 видно, что фазовая скорость электромагнитной волны равна
видно, что фазовая скорость электромагнитной волны равна 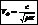 . В вакууме фазовая скорость равна
. В вакууме фазовая скорость равна  . Получается, что поле может существовать в виде электромагнитной волны, даже когда нет ничего.
. Получается, что поле может существовать в виде электромагнитной волны, даже когда нет ничего.



 .
. .
.


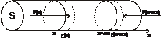 Масса газа, находящегося в этом объеме, равна:
Масса газа, находящегося в этом объеме, равна:
 – смещение левой границы.
– смещение левой границы. по сравнению с характерными размерами области сжатия и разряжения.
по сравнению с характерными размерами области сжатия и разряжения. . Масса слоя не измениться.
. Масса слоя не измениться.
 – отклонение от равновесия в окрестности
– отклонение от равновесия в окрестности 



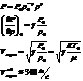

 .
. – смещение.
– смещение. – скорость смещения.
– скорость смещения. – относительная деформация.
– относительная деформация.

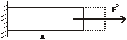






 силы
силы  и
и  совершают работу.
совершают работу.

 – плотность потока энергии.
– плотность потока энергии.
 – вектор Умова.
– вектор Умова. .
. .
.
 , что
, что 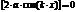 , это будут
, это будут  .
.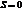 или
или  , но эти точки не подвижны.
, но эти точки не подвижны. , почему же она равна нулю?
, почему же она равна нулю? , а у нас другой вид волн, поэтому фазовую скорость мы находим по определению.
, а у нас другой вид волн, поэтому фазовую скорость мы находим по определению. . Запишем волновое уравнение как второй закон Ньютона. (т.к. в колебании нет переноса массы, то колебание идёт вдоль оси
. Запишем волновое уравнение как второй закон Ньютона. (т.к. в колебании нет переноса массы, то колебание идёт вдоль оси  ).
).
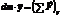 .
. - силы со стороны других кусков равны по модулю. Тогда:
- силы со стороны других кусков равны по модулю. Тогда: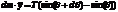 ,
,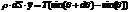 ,
, - длина колеблющегося кусочка струны. Пусть величина отклонения струны мала по сравнению с длиной всей струны. Тогда можно записать следующие выражения:
- длина колеблющегося кусочка струны. Пусть величина отклонения струны мала по сравнению с длиной всей струны. Тогда можно записать следующие выражения: ,
, - дифференциал длины дуги, т.к.
- дифференциал длины дуги, т.к.  то
то  мала и
мала и  .
.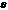 мал, откуда имеем:
мал, откуда имеем: .
. ,
, - уравнение движения кусочка струны, откуда
- уравнение движения кусочка струны, откуда 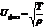 .
. .
.
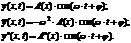 Подставим эти выражения в волновое уравнение, тогда:
Подставим эти выражения в волновое уравнение, тогда: ,
, .
.
 - константы интегрирования. Найдем их из начальных условий:
- константы интегрирования. Найдем их из начальных условий: .
.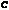 не равно нулю (т.к. тогда не будет никаких волн вообще), то имеем, что
не равно нулю (т.к. тогда не будет никаких волн вообще), то имеем, что
 .
. не может быть каким угодно, а они существуют только при определённых дискретных
не может быть каким угодно, а они существуют только при определённых дискретных  .
. .
. ,
, .
. - сфотографировали при
- сфотографировали при  , это уравнение показывает начальное положение струны, её начальную форму.
, это уравнение показывает начальное положение струны, её начальную форму. - скорость по
- скорость по  кусочка струны, показывает силу приложенную в начале.
кусочка струны, показывает силу приложенную в начале.


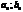 найдём
найдём  .
. определяет форму струны в начальный момент времени. Итак, нам известны две функции
определяет форму струны в начальный момент времени. Итак, нам известны две функции
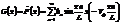 ,
, - фазовая скорость. Нам необходимо найти
- фазовая скорость. Нам необходимо найти  и
и  .
. и проинтегрируем от
и проинтегрируем от  до
до  .
. В правой части суммирование и интегрирование идет по разным переменным, поэтому можно преобразовать выражение.
В правой части суммирование и интегрирование идет по разным переменным, поэтому можно преобразовать выражение. Все интегралы
Все интегралы  равны нулю кроме случая
равны нулю кроме случая 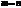 .
.

 аналогично можно найти и
аналогично можно найти и  .
. можно легко найти
можно легко найти  и
и  .
. ,
,  при
при  .
.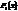 и
и  - линейные, причем
- линейные, причем ,
, 

 ,
, 

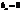 .
. Проинтегрировав по частям, получим
Проинтегрировав по частям, получим  . В нашем случае
. В нашем случае  ,
,  ,
, 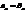 . Введем обозначения
. Введем обозначения 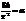 и рассмотрим несколько первых членов
и рассмотрим несколько первых членов 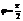 ,
,  ,
,  ,
,  ,
,  ,
,  , …
, …
 . Если струну оттянули слабо, то
. Если струну оттянули слабо, то  мало, и можно ограничиться первым слагаемым:
мало, и можно ограничиться первым слагаемым:  .
. не зависит от
не зависит от  . Это можно объяснить тем, что
. Это можно объяснить тем, что 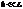 .
.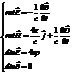
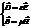 и уравнения Максвелла теперь выглядят так:
и уравнения Максвелла теперь выглядят так: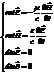



 .
.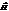 можно провести те же самые рассуждения
можно провести те же самые рассуждения  .
. .
. и
и 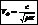 . В вакууме фазовая скорость равна
. В вакууме фазовая скорость равна  . Получается, что поле может существовать в виде электромагнитной волны, даже когда нет ничего.
. Получается, что поле может существовать в виде электромагнитной волны, даже когда нет ничего.

