

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|

Упражнение. Интерпретировать умножение и деление в тригонометрической форме геометрически.
ИЗВЛЕЧЕНИЕ КОРНЯ
ИЗ КОМПЛЕКСНОГО ЧИСЛА.
Пусть z = a+bi.
Надо извлечь корень из z.
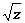 —?
—?
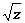 обозначим через z1, то z
обозначим через z1, то z  = z.
= z.
Пусть z1 = x+iy, тогда
(x2–y2)+2xyi = a+bi,

Решив эту систему, мы найдем подходящие значения z1.
Если так действовать и для извлечения корней более высокой степени, то придётся уметь решать уравнения соответствующих степеней.
Для извлечения корня из комплексного числа хорошо приспособлена тригонометрическая форма комплексного числа.
Пусть z = r(cosj+i sinj), надо найти  = z1, положим
= z1, положим
z1=ρ (cosy+i siny), z  ==ρn(cos(ny)+i sin(ny), r = ρn Þ ρ =
==ρn(cos(ny)+i sin(ny), r = ρn Þ ρ = 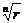 , j = ny+2pk
, j = ny+2pk  y =
y = 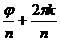 .
.
Получим
 =
= 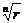 (cos
(cos  +i sin
+i sin  ) (1),
) (1),
где k — любое целое число, то есть корень n–той степени из произвольного комплексного числа z всегда существует и его можно посчитать по формуле (1), причем формула (1) даёт все корни, если k пробегает множество целых чисел (достаточно ограничиться k = 0,…, n–1)
Если возьмем k – любое, то мы можем разделить его с остатком на n:
k = nq+s; 0£s£n–1
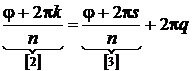 .
.
Углы [2] и [3] отличаются на кратное 2p, и поэтому косинусы и синусы от них совпадают, следовательно формула (1) при угле [2] и при угле [3] даёт одинаковое значение.
Если брать k от 0 до n–1, то мы получим все значения. Нетрудно заметить, что все эти значения разные (смотри геометрическую интерпретацию).
Теорема 4.
Извлечение корня степени n из комплексного числа всегда возможно, и даёт n различных значений, получающихся по формуле (1).
Теорема нами доказана ранее.
Замечание (геометрическая интерпретация).
Все значения  расположены на окружности радиуса
расположены на окружности радиуса  с центром в начале координат и делят окружность на n равных частей:
с центром в начале координат и делят окружность на n равных частей:
|
|

§5. КОРНИ ИЗ ЕДИНИЦЫ.
1 = cos0+i sin0 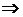
 = cos
= cos  +i sin
+i sin  ,
,  .
.
Корни расположены на окружности единичного радиуса и делят эту окружность на n равных частей.
Теорема 1.
Все значения корня n–той степени из комплексного числа z можно получить умножением одного из них на все корни из 1.
Доказательство:
Возьмём a =  =
= 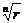 (cos
(cos  +i sin
+i sin  ), где s–фиксированное число.
), где s–фиксированное число.
e1, e2,…, en – так обозначим все корни  .
.
Домножим каждый из корней e1,…, en на a. Они разные, все являются корнями n–той степени из z, ибо (aei)n = z и их  штук.
штук.
Теорема доказана.
Теорема 2.
Произведение двух корней n–той степени из единицы есть корень степени n из единицы.
Следствие.
Степень корня n–той степени из единицы есть корень степени n из единицы.
Все ли корни из 1 равноправны?
n=4; 1, –1, i, –i — корни из единицы.
i; –i — первообразные корни; если i возводить в степени 0, 1, 2, 3, то получим все корни.
Определение 1.
Корень n–той степени из 1 называется первообразным, если он не даёт единицу в степени меньше, чем n.
Всегда ли есть первообразный корень?
Всегда! Например: cos  +i sin
+i sin  .
.
Упражнение. Доказать, что корень n–той степени
ek = cos  + i sin
+ i sin  будет первообразным, если n и k — взаимно простые (не имеют общих делителей отличных от 1).
будет первообразным, если n и k — взаимно простые (не имеют общих делителей отличных от 1).
ЧИСЛОВОЕ ПОЛЕ.
В множествах Q Ì R Ì C возможны четыре операции +, –, ×,:.
Определение 1. Подмножество K Ì C множества комплексных чисел C, состоящее более, чем из одного элемента, называют числовым полем, если выполняются следующие условия:
1) " a, bÎK Þ a+bÎK, то есть в множестве K всегда возможно сложение;
2) " aÎK Þ –aÎK;
3) " a, bÎK Þ abÎK, то есть задано умножение в K (K замкнуто относительно умножения);
4) " a ¹ 0; a -1ÎK.
Из 2) с учётом 1) получаем, что в K всегда возможно вычитание.
Из 4) с учётом 3) получаем, что в K всегда возможно деление на число не равное 0.
Q — поле рациональных чисел;
R — поле вещественных чисел;
C — поле комплексных чисел.
|
|
|

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!