Пример 6. Установить, при каких значениях переменных не имеет смысла дробь  .
.
Решение.  . Мы получили равенство двух переменных, приведем числовые примеры:
. Мы получили равенство двух переменных, приведем числовые примеры:  или
или 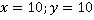 и т. д.
и т. д.
Изобразим это решение на графике в декартовой системе координат:

Рис. 3.
График функции  .
.
Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.
Ответ.  .
.
5. Случай типа "деление на ноль"
В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа  .
.
Пример 7. Установить, при каких значениях переменных не имеет смысла дробь  .
.
Решение.  .
.
Получается, что дробь не имеет смысла при  . Но можно возразить, что это не так, потому что:
. Но можно возразить, что это не так, потому что:  .
.
Может показаться, что если конечное выражение равно 8 при  , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при
, то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при  . Однако, если подставить
. Однако, если подставить  в исходное выражение, то получим
в исходное выражение, то получим  – не имеет смысла.
– не имеет смысла.
Ответ.  .
.
Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях  указанная дробь равна нулю?
указанная дробь равна нулю?
 (дробь равна нулю, когда ее числитель равен нулю)
(дробь равна нулю, когда ее числитель равен нулю)  . Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при
. Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при  , т. к. при этом значении переменной знаменатель равен нулю. Значит, данное уравнение имеет только один корень
, т. к. при этом значении переменной знаменатель равен нулю. Значит, данное уравнение имеет только один корень  .
.
Правило нахождения ОДЗ
Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби: для нахождения ОДЗ дроби необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения.
Мы рассмотрели две основные задачи: вычисление значения дроби при указанных значениях переменных и нахождение области допустимых значений дроби.
Рассмотрим теперь еще несколько задач, которые могут возникнуть при работе с дробями.
Разные задачи и выводы
Пример 8. Докажите, что при любых значениях переменной дробь  .
.
Доказательство. Числитель – число положительное.  . В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.
. В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.
Доказано.
Пример 9. Известно, что 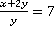 , найти
, найти  .
.
Решение. Поделим дробь почленно  . Сокращать на
. Сокращать на  мы имеем право, с учетом того, что
мы имеем право, с учетом того, что  является недопустимым значением переменной для данной дроби.
является недопустимым значением переменной для данной дроби.
Ответ.  .
.
На данном уроке мы рассмотрели основные понятия, связанные с дробями. На следующем уроке мы рассмотрим основное свойство дроби.
Домашнее задание
1. Запишите рациональную дробь, областью определения которой является: а) множество  , б) множество
, б) множество  , в) вся числовая ось.
, в) вся числовая ось.
2. Докажите, что при всех допустимых значениях переменной  значение дроби
значение дроби  неотрицательно.
неотрицательно.
3. Найдите область определения выражения  . Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.
. Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.
Урок 8: Основное свойство алгебраической дроби.
На данном уроке будет рассмотрено основное свойство алгебраической дроби. Умение правильно и без ошибок применять это свойство является одним из важнейших базовых умений во всем курсе школьной математики и будет встречаться не только на протяжении изучения данной темы, но и практически во всех изучаемых в дальнейшем разделах математики. Ранее уже было изучено сокращение обыкновенных дробей, а на данном уроке будет рассмотрено сокращение рациональных дробей. Несмотря на довольно большое внешнее отличие, существующее между рациональными и обыкновенными дробями, у них очень много общего, а именно – и обыкновенным, и рациональным дробям присущи одинаковое основное свойство и общие правила выполнения арифметических действий. В рамках урока мы столкнемся с понятиями: сокращение дроби, умножение и деление числителя и знаменателя на одно и то же выражение – и рассмотрим примеры.





 .
. . Мы получили равенство двух переменных, приведем числовые примеры:
. Мы получили равенство двух переменных, приведем числовые примеры:  или
или 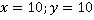 и т. д.
и т. д.
 .
. .
. .
. .
. .
. . Но можно возразить, что это не так, потому что:
. Но можно возразить, что это не так, потому что:  .
. – не имеет смысла.
– не имеет смысла. .
. указанная дробь равна нулю?
указанная дробь равна нулю? (дробь равна нулю, когда ее числитель равен нулю)
(дробь равна нулю, когда ее числитель равен нулю)  . Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при
. Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при  .
. .
. . В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.
. В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.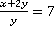 , найти
, найти  .
. . Сокращать на
. Сокращать на  является недопустимым значением переменной для данной дроби.
является недопустимым значением переменной для данной дроби. .
. , б) множество
, б) множество  , в) вся числовая ось.
, в) вся числовая ось. значение дроби
значение дроби  неотрицательно.
неотрицательно. . Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.
. Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.


