Напомним определение многочлена: многочленом называют алгебраическую сумму одночленов.
Пример: 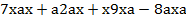
Мы знаем, что каждый одночлен можно привести к стандартному виду, выполним это:
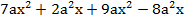
Напомним, что если у одночленов одинаковая буквенная часть – то их можно складывать, таким образом, приводя многочлен к стандартному виду:
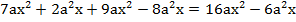
Полученный многочлен можно разложить на множители, в данном случае методом вынесения общего множителя:
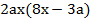
Напомним, что, при вынесении общего множителя, на него делится каждый член многочлена и результат записывается в скобках, а общий множитель –за скобками.
Разложение многочлена на множители, вынесение общего множителя
Многочлены можно складывать, вычитать, умножать, возводить в степень. Рассмотрим примеры:
Пример 1: найти 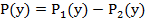 :
:
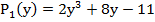
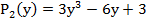
Итак, выполним требуемое действие:

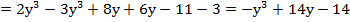
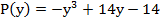
Пример 2: вычислить значение выражения при 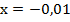 :
:
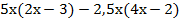
Напомним, что для умножения многочлена на одночлен нужно каждый член многочлена умножить на одночлен:
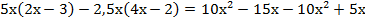
Приведем в полученном выражении подобные члены:
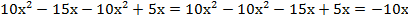
Подставим заданное значение х:
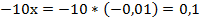
Вспомним операцию деления многочлена на одночлен.
Пример 3:
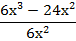
1 способ: разделить каждый член многочлена на одночлен:
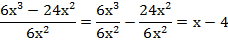
Необходимо отметить, что 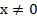 , в противном случае данное выражение не имеет смысла.
, в противном случае данное выражение не имеет смысла.
2 способ: разложить числитель на множители и сократить дробь:
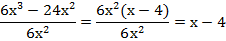
Пример 4: решить уравнение:
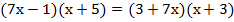
Напомним, что для умножения многочлена на многочлен нужно каждый член первого многочлена умножить на каждый член второго многочлена:
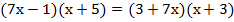
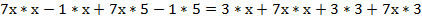
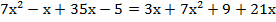
Приведем подобные члены, соберем неизвестные слева, а свободные члены – справа:
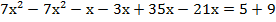
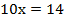
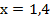
Решение типовых задач
Одна из типовых задач – текстовые задачи, где нужно сначала составить уравнение, а потом его решить.
Пример 5: найдите 4 последовательных натуральных числа, если известно, что разность между произведением двух больших и двух меньших чисел равна 58.
Для решения задачи применим метод математического моделирования.
Этап 1 – составление математической модели:
Обозначим первое из четырех чисел за 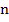 , тогда остальные числа запишем как
, тогда остальные числа запишем как  ,
, 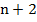 ,
, 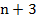 , так как первое из четырех последовательных натуральных чисел является наименьшим, а каждое следующее отличается от предыдущего на единицу. Произведение двух больших чисел в таком случае равно
, так как первое из четырех последовательных натуральных чисел является наименьшим, а каждое следующее отличается от предыдущего на единицу. Произведение двух больших чисел в таком случае равно 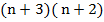 , а произведение двух меньших –
, а произведение двух меньших – 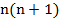 . В условии сказано, что разность между произведением двух больших и двух меньших чисел равна 58. Составим уравнение:
. В условии сказано, что разность между произведением двух больших и двух меньших чисел равна 58. Составим уравнение:
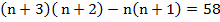
Математическая модель составлена.
Этап 2 – работа с математической моделью:
В данном случае работа заключается в решении линейного уравнения с одним неизвестным. Для этого упростим составленное выражение, выполним умножение:
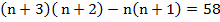

Соберем неизвестные слева, а свободные члены – справа и приведем подобные:
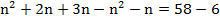
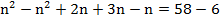
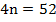
Из полученного элементарного уравнения найдем n:
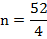
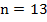
Этап 3 – ответ на вопрос задачи:
Было задано найти четыре последовательных натуральных числа, удовлетворяющих условию. Первое из чисел мы обозначили за n, нашли 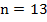 , таким образом, нужная нам последовательность – это числа: 13, 14, 15, 16.
, таким образом, нужная нам последовательность – это числа: 13, 14, 15, 16.
Выводы по уроку
Вывод: на данном уроке мы вспомнили определение многочлена и основы работы с многочленами – приведение к стандартному виду и арифметические операции. Кроме того, мы рассмотрели типовые задачи – вычислительную, текстовую задачи и уравнение.
Домашнее задание.
1. Найти сумму и разность многочленов:
а) (х² + 4х) – (х² – 4х); б)(5х² + 3х) + (х²-7 – 3х);
в) (х³ + 1,3х² - 2х) – (1,3х + 2х²).
2. Выполнить действия:
а) –х(х² - 3х); б) (х – 2)(х + 3); в) 16а³ - 2а²(8а – 3);
г) (9 + а² - 3а)(а² + 3а).
3. Решить уравнение:
а)  ; б) (3 – х)(х + 4) + х² = 0.
; б) (3 – х)(х + 4) + х² = 0.
4. Упростить выражение: 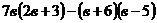 .
.
Урок 4: Повторение. Формулы сокращенного умножения.
На данном уроке мы вспомним формулы сокращенного умножения, их предназначение и смысл. Мы решим несколько примеров на закрепление материала.





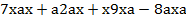
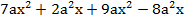
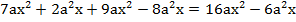
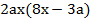
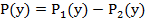 :
: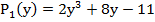
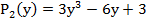

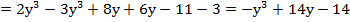
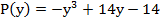
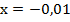 :
: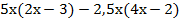
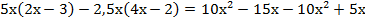
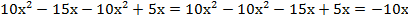
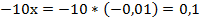
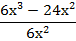
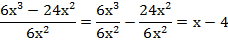
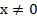 , в противном случае данное выражение не имеет смысла.
, в противном случае данное выражение не имеет смысла.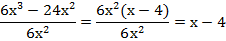
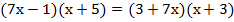
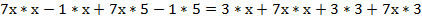
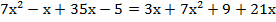
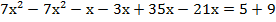
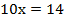
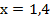
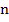 , тогда остальные числа запишем как
, тогда остальные числа запишем как  ,
, 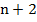 ,
, 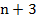 , так как первое из четырех последовательных натуральных чисел является наименьшим, а каждое следующее отличается от предыдущего на единицу. Произведение двух больших чисел в таком случае равно
, так как первое из четырех последовательных натуральных чисел является наименьшим, а каждое следующее отличается от предыдущего на единицу. Произведение двух больших чисел в таком случае равно 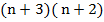 , а произведение двух меньших –
, а произведение двух меньших – 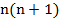 . В условии сказано, что разность между произведением двух больших и двух меньших чисел равна 58. Составим уравнение:
. В условии сказано, что разность между произведением двух больших и двух меньших чисел равна 58. Составим уравнение: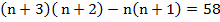

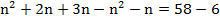
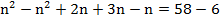
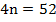
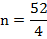
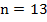
 ; б) (3 – х)(х + 4) + х² = 0.
; б) (3 – х)(х + 4) + х² = 0.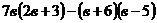 .
.

