О. Уравнение вида  , где
, где  – переменная
– переменная  ,
,  называется квадратным.
называется квадратным.
О. Если  , то уравнение называется приведенным квадратным уравнением.
, то уравнение называется приведенным квадратным уравнением.
О. Квадратное уравнение, в котором хотя бы один из коэффициентов  или
или  равен
равен 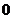 , называется неполным квадратным уравнением
, называется неполным квадратным уравнением
Выведем формулу корней квадратного уравнения в общем случае:
 ,
, 
Поделим обе части уравнения на  . При этом корни уравнения не изменятся (почему?).
. При этом корни уравнения не изменятся (почему?).

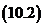
Выделим полный квадрат:

О. Выражение:  называется дискриминантом квадратного уравнения, и обозначается через
называется дискриминантом квадратного уравнения, и обозначается через  , тогда уравнение можно записать так:
, тогда уравнение можно записать так:
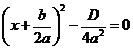
Возможны следующие 3 случая:
1. Если  , то из дискриминанта можно извлечь корень (почему?), тогда получаем решения уравнения:
, то из дискриминанта можно извлечь корень (почему?), тогда получаем решения уравнения:

 или
или 
То есть

 или
или 

 или
или 
Эти две формулы можно объединить в следующую:
 - эта формула называется формулой корней квадратного уравнения
- эта формула называется формулой корней квадратного уравнения
2. Если  , то уравнение
, то уравнение 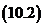 примет вид:
примет вид:

В этом случае уравнение имеет один корень.
Замечание: можно также сказать, что в этом случае квадратное уравнение имеет два совпадающих корня.
3. Если 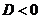 , то значение дроби
, то значение дроби  , поэтому уравнение
, поэтому уравнение 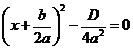 , а значит и уравнение
, а значит и уравнение  не имеет корней (почему?).
не имеет корней (почему?).
Таким образом,
Если  , то уравнение
, то уравнение  имеет 2 различных корня:
имеет 2 различных корня: 
Если  , то уравнение
, то уравнение  имеет 2 совпадающих корня:
имеет 2 совпадающих корня: 
Если 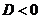 , то уравнение
, то уравнение  корней не имеет.
корней не имеет.
Теорема Виета.
Пусть дано уравнение  ,
,  – корни уравнения, тогда
– корни уравнения, тогда

Доказательство:
Пусть уравнение  имеет 2 различных корня (
имеет 2 различных корня ( ):
):



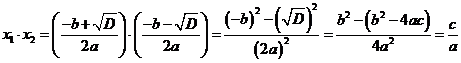
Итак, действительно 

Замечание: Если рассмотреть приведенное квадратное уравнение  , то формулы Виета будут выглядеть так:
, то формулы Виета будут выглядеть так:  .
.
В школьном курсе математики чаще всего формулы Виета применяются именно для приведенного квадратного уравнения.
Имеет место теорема, обратная теореме Виета:
Если числа 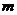 и
и  таковы, что
таковы, что 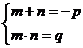
То эти числа являются корнями уравнения 
Доказательство:
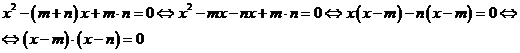
Значит, числа 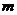 и
и  действительно являются корнями уравнения
действительно являются корнями уравнения  .
. 
Замечание: теорема, обратная теореме Виета, позволяет составлять квадратные уравнения по его корням.
Например, если  , то
, то  , тогда эти числа являются корнями уравнения
, тогда эти числа являются корнями уравнения 
16. Разложение квадратного трехчлена на линейные множители
О. Многочлен вида: 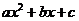 , где
, где  – переменная
– переменная  ,
,  называется квадратным трехчленом.
называется квадратным трехчленом.
О.Корнем квадратного трехчлена называется значение переменной, при которой значение этого трехчлена равно нулю.
Теорема.
Если  и
и  – корни квадратного трёхчлена
– корни квадратного трёхчлена 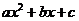 , то
, то 
Доказательство:
Вынесем за скобки в многочлене  множитель а. Получим:
множитель а. Получим:  . Так как корни квадратного трёхчлена
. Так как корни квадратного трёхчлена  являются корнями квадратного уравнения
являются корнями квадратного уравнения  , то, по теореме Виета,
, то, по теореме Виета,  ,
,  .
.
Поэтому

Итак, 

Если квадратный трёхчлен имеет один корень (два совпадающих корня), то формула  примет вид
примет вид  , где
, где  - корень квадратного трёхчлена.
- корень квадратного трёхчлена.
Заметим, что если квадратный трёхчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
17. Формулы сокращенного умножения.

Доказательство:


( ,т.к. по определению произведения многочленов, операции над многочленами обладают свойствами коммутативности, ассоциативности и дистрибутивности.)
,т.к. по определению произведения многочленов, операции над многочленами обладают свойствами коммутативности, ассоциативности и дистрибутивности.) 

Доказательство:

 .
. 

Доказательство:
 .
. 

Доказательство:

 .
. 
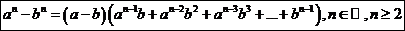
Доказательство:
Пусть  , рассмотрим произведение
, рассмотрим произведение



Доказательство:

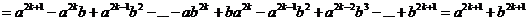

18. Свойства числовых неравенств.
О. Число 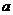 больше числа
больше числа  , если разность
, если разность  – положительное число; число
– положительное число; число 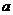 меньше числа
меньше числа  , если разность
, если разность  – отрицательное число.
– отрицательное число.
Теорема 1.
Если  , то
, то  ; если
; если  , то
, то  .
.
Доказательство.
Если  , то по определению разность
, то по определению разность  – положительное число, тогда разность
– положительное число, тогда разность  - отрицательное число, а это значит, по определению, что
- отрицательное число, а это значит, по определению, что  . И наоборот.
. И наоборот. 
Теорема 2.
Если  и
и  , то
, то  .
.
Доказательство.
По условию  и
и  , значит, по определению разность
, значит, по определению разность  – отрицательное число и разность
– отрицательное число и разность  – отрицательное число. Сумма отрицательных чисел – число отрицательное, поэтому сумма
– отрицательное число. Сумма отрицательных чисел – число отрицательное, поэтому сумма  – отрицательна. Преобразуем эту сумму
– отрицательна. Преобразуем эту сумму  . Следовательно, разность
. Следовательно, разность  – отрицательна и, по определению,
– отрицательна и, по определению,  .
. 
Теорема 3.
Если  и
и  – любое число, то
– любое число, то  .
.
Доказательство.
Преобразуем разность  . По условию,
. По условию,  , поэтому
, поэтому  – отрицательное число. Значит, и разность
– отрицательное число. Значит, и разность  - отрицательна. Следовательно,
- отрицательна. Следовательно,  .
. 
Теорема 4.
Если  и
и  – положительное число, то
– положительное число, то  ,
,
Если  и
и  – отрицательное число, то
– отрицательное число, то  ,
,
Доказательство.
Преобразуем разность  . Так как
. Так как  , то разность
, то разность  – отрицательное число. Если
– отрицательное число. Если  , то произведение
, то произведение  – отрицательно, и, следовательно,
– отрицательно, и, следовательно,  . Если
. Если  , то произведение
, то произведение  – положительно, и, следовательно,
– положительно, и, следовательно,  .
. 
Следствие.
Если 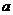 и
и  – положительные числа и
– положительные числа и  , то
, то  .
.
Доказательство.
Разделим обе части неравенства  на положительное число
на положительное число  :
:  .
.
Сократив дробь, получим, что  , т.е.
, т.е.  .
. 
Теорема 5.
Если  и
и 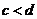 , то
, то 
Доказательство.
Прибавим к обеим частям неравенства  числ о
числ о  , получим
, получим  .
.
Прибавим к обеим частям неравенства 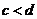 число
число  , получим
, получим  .
.
Из неравенств  и
и  , и теоремы 2 следует, что
, и теоремы 2 следует, что 

Теорема 6.
Если  и
и 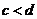 , где
, где 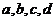 – положительные числа, то
– положительные числа, то  .
.
Доказательство.
Умножим обе части неравенства  на положительное число
на положительное число  , получим неравенство
, получим неравенство  .
.
Умножим обе части неравенства 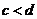 на положительное число
на положительное число  , получим неравенство
, получим неравенство 
Из неравенств  и
и  и теоремы 2 следует, что
и теоремы 2 следует, что  .
. 
19. Свойства числовых равенств.
Числовым равенством называется числовое выражение, содержащее знак 
Свойство 1.

(если к обеим частям верного числового равенства прибавить одно и то же число, то получится также верное числовое равенство)
Свойство 2.

(если из одной части верного числового равенства перенести в другую часть слагаемое с противоположным знаком, то получится также верное числовое равенство)
Свойство 3.

(если обе части верного числового равенства умножить на одно и то же число, то получится также верное числовое равенство)
Свойство 4.

(если обе части верного числового равенства возвести в одну и ту же натуральную степень, то получится также верное числовое равенство)
20. Метод интервалов
О. Метод интервалов – метод решения рациональных неравенств.
Этот метод основан на следующей теореме математического анализа
(теореме Больцано-Коши), которую мы рассмотрим без доказательства:
Пусть функция  на отрезке
на отрезке  и на концах его принимает разные по знаку значения,
и на концах его принимает разные по знаку значения,



 , где
, где  – переменная
– переменная  ,
,  называется квадратным.
называется квадратным. , то уравнение называется приведенным квадратным уравнением.
, то уравнение называется приведенным квадратным уравнением. или
или  равен
равен 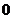 , называется неполным квадратным уравнением
, называется неполным квадратным уравнением

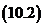

 называется дискриминантом квадратного уравнения, и обозначается через
называется дискриминантом квадратного уравнения, и обозначается через  , тогда уравнение можно записать так:
, тогда уравнение можно записать так: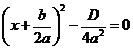
 , то из дискриминанта можно извлечь корень (почему?), тогда получаем решения уравнения:
, то из дискриминанта можно извлечь корень (почему?), тогда получаем решения уравнения:
 или
или 
 или
или 
 или
или 
 - эта формула называется формулой корней квадратного уравнения
- эта формула называется формулой корней квадратного уравнения , то уравнение
, то уравнение 
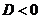 , то значение дроби
, то значение дроби  , поэтому уравнение
, поэтому уравнение 
 – корни уравнения, тогда
– корни уравнения, тогда



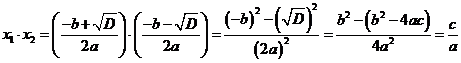

 , то формулы Виета будут выглядеть так:
, то формулы Виета будут выглядеть так:  .
.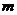 и
и  таковы, что
таковы, что 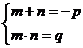
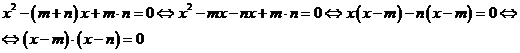
 , то
, то  , тогда эти числа являются корнями уравнения
, тогда эти числа являются корнями уравнения 
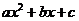 , где
, где  и
и  – корни квадратного трёхчлена
– корни квадратного трёхчлена 
 множитель а. Получим:
множитель а. Получим:  . Так как корни квадратного трёхчлена
. Так как корни квадратного трёхчлена  , то, по теореме Виета,
, то, по теореме Виета,  ,
,  .
.


 , где
, где  - корень квадратного трёхчлена.
- корень квадратного трёхчлена.


 ,т.к. по определению произведения многочленов, операции над многочленами обладают свойствами коммутативности, ассоциативности и дистрибутивности.)
,т.к. по определению произведения многочленов, операции над многочленами обладают свойствами коммутативности, ассоциативности и дистрибутивности.) 

 .
. 
 .
. 

 .
. 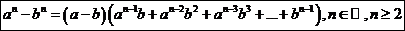
 , рассмотрим произведение
, рассмотрим произведение


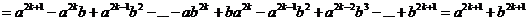
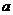 больше числа
больше числа  – положительное число; число
– положительное число; число  , то
, то  ; если
; если  , то
, то  .
. - отрицательное число, а это значит, по определению, что
- отрицательное число, а это значит, по определению, что  , то
, то  .
. – отрицательное число. Сумма отрицательных чисел – число отрицательное, поэтому сумма
– отрицательное число. Сумма отрицательных чисел – число отрицательное, поэтому сумма  – отрицательна. Преобразуем эту сумму
– отрицательна. Преобразуем эту сумму  . Следовательно, разность
. Следовательно, разность  – отрицательна и, по определению,
– отрицательна и, по определению,  .
. . По условию,
. По условию,  ,
, ,
, . Так как
. Так как  , то произведение
, то произведение  – отрицательно, и, следовательно,
– отрицательно, и, следовательно,  , то произведение
, то произведение  .
. на положительное число
на положительное число  :
:  .
. , т.е.
, т.е.  .
. 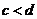 , то
, то 
 .
.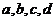 – положительные числа, то
– положительные числа, то  .
. .
.





 на отрезке
на отрезке  и на концах его принимает разные по знаку значения,
и на концах его принимает разные по знаку значения,


